Розв’язування

1-ий спосіб. Обчислимо ротор векторного поля:

.

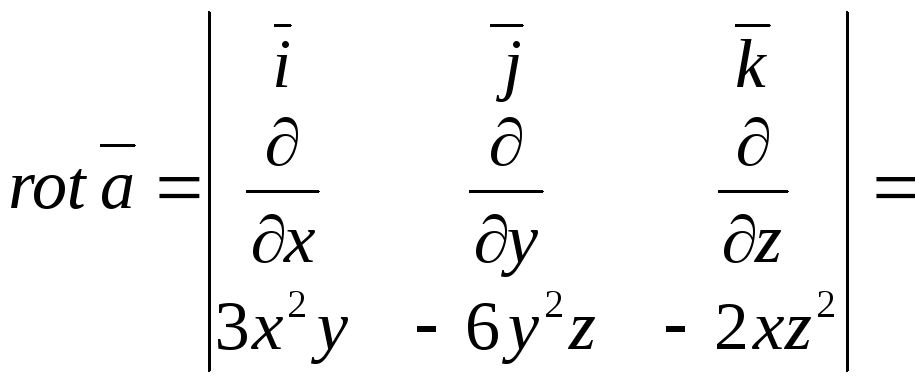
Обчислимо за формулою:

.

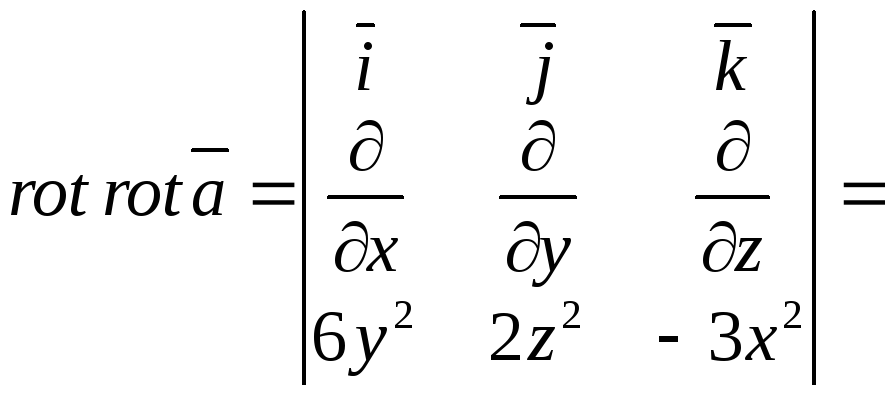
2-ий спосіб. Використаємо формулу (3.23). Для цього знайдемо спочатку , маємо:

. Тоді

.

Оскільки , маємо:

3.6 Властивості ротора векторного поля

1. Якщо – сталий вектор, то .

2. (Властивість лінійності). Якщо і – векторні поля, і – числа, то

.

3. Для будь-якого векторного поля .

Дійсно:

, оскільки

.

4. Нехай – скалярне поле, – векторне поле. Побудуємо векторне поле , тоді .

Дійсно: , ,

,

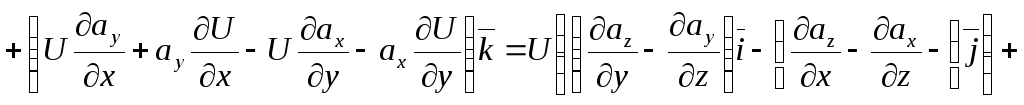
або

Зауваження. Якщо вектор – постійний, то

5. Нехай і , тоді .

Дійсно,

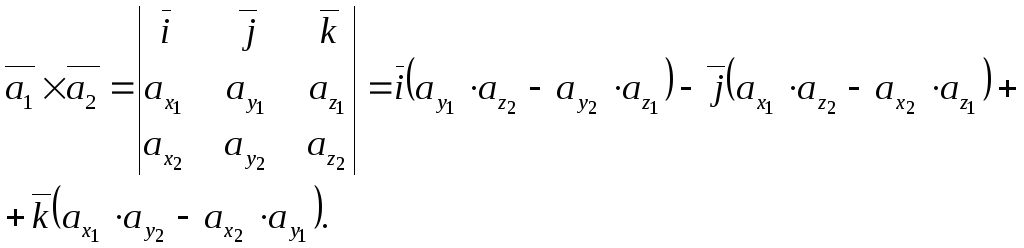
Тоді

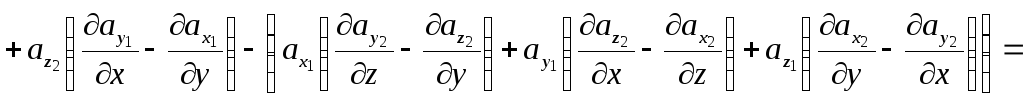
або

Приклад 3.7 Довести, що , де – сталий вектор.

Розв’язування

Нехай , де – сталий вектор.

Обчислимо :

.

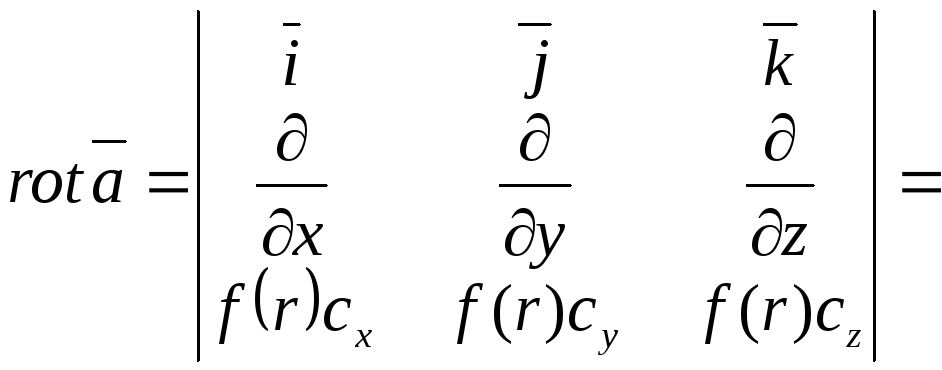
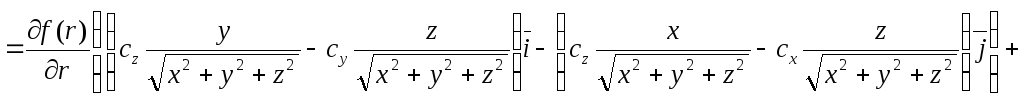
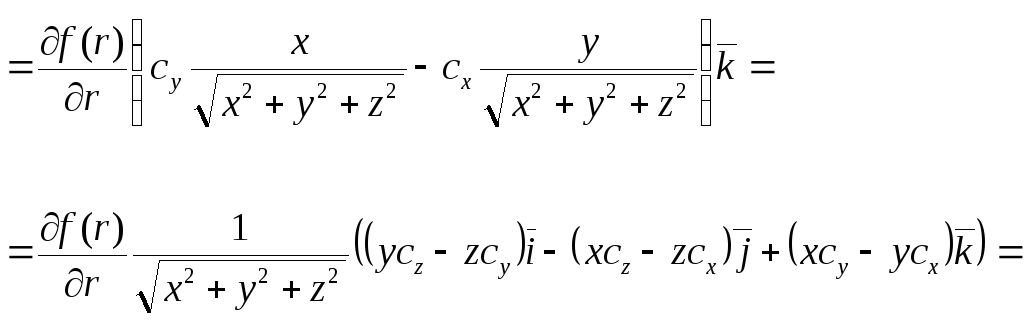
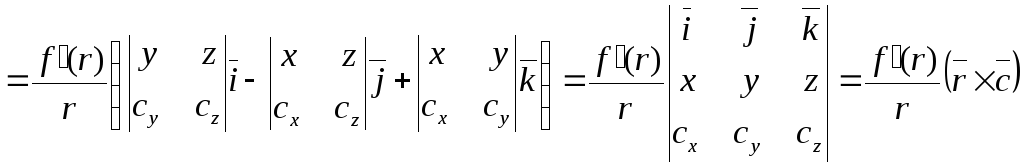3.7 Циркуляція векторного поля та її обчислення. Формула Стокса

Нехай маємо векторне поле і – деяка гладка поверхня. Як відмічалося в пункті 3.3 циркуляцією векторного поля називають криволінійний інтеграл цього поля, обчислений вздовж довільного замкнутого контура, який належить поверхні , і позначають його . Для розуміння фізичної суті поняття циркуляції розглянемо поняття криволінійного інтеграла та методи його обчислення.

Нехай точка рухається уздовж деякої лінії від точки до точки . Тоді робота, що її виконує сила при переміщенні точки уздовж лінії , називається криволінійним інтегралом і обчислюється за формулою:

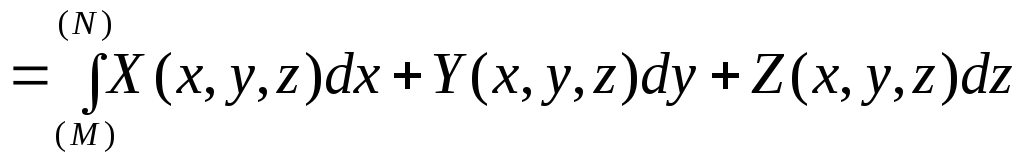. (3.24)

При цьому напрям від точки до точки називається напрямом інтегрування.

Зауваження. Для позначення криволінійного інтеграла вздовж замкненого контура (точка початку збігається з точкою кінця) використовують символ , тобто . Слід відмітити, що замкнутий контур вважається додатно орієнтованим, якщо при його обході область, обмежена цим контуром, залишається зліва.

Обчислити криволінійні інтеграли можна шляхом зведення їх до визначених інтегралів, і вони мають аналогічні властивості.

Нехай крива (від точки до точки ) задана параметричним рівнянням , , де функції , та на відрізку неперервні разом із своїми похідними , і . Точці відповідає значення параметра , а точці – . Тоді

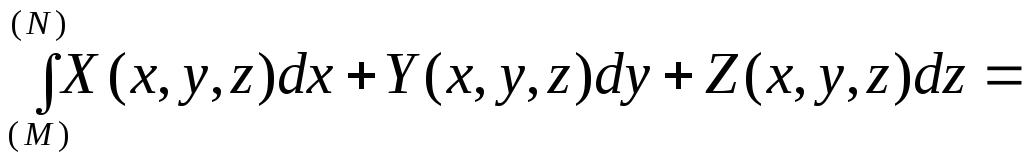
. (3.25)

Приклад 3.8 Обчислити інтеграл , де – частина кола , , що знаходиться у першому квадранті.

Розв’язування

Для обчислення даного інтеграла використаємо формулу (3.25). Знайдемо відповідні похідні

, .

Тоді

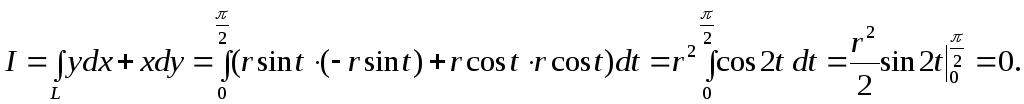
Зокрема, якщо крива (від точки до точки ) задана рівнянням , , де функція та її похідна неперервні на відрізку , то з формули (3.25) дістанемо

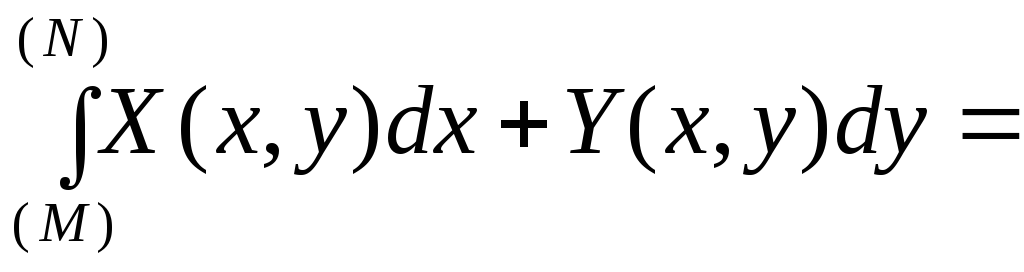
. (3.26)

Приклад 3.9 Обчислити інтеграл , де – дуга параболи від точки до точки .