
- •Тема 1 скалярне поле та його характеристики 5
- •Тема 2 поняття векторного поля та його потоку 16
- •Тема 3 характеристики векторного поля 41
- •Тема 4 сПеЦіальні типи полів 79
- •Передмова
- •Тема 1 скалярне поле та його характеристики
- •1.1 Похідна за напрямом
- •Розв’язування
- •1.2 Поняття та властивості градієнта
- •Доведення
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 поняття векторного поля та його потоку
- •2.1 Потік векторного поля
- •2.2 Обчислення потоку векторного поля
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.3 Формула Остроградського-Гаусса
- •Розв’язування
- •Р озв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 характеристики векторного поля
- •3.1 Дивергенція (розбіжність) векторного поля
- •3.2 Обчислення дивергенції векторного поля в декартовій системі координат
- •Розв’язування
- •Розв’язування
- •3.3 Проекція ротора векторного поля на вектор нормалі та ротор векторного поля
- •Розв’язування
- •Розв’язування
- •3.4. Оператор Гамільтона
- •Розв’язування
- •3.5 Диференціальні операції другого порядку
- •Розв’язування
- •3.6 Властивості ротора векторного поля
- •Розв’язування
- •3.7 Циркуляція векторного поля та її обчислення. Формула Стокса
- •Розв’язування
- •Розв’язування
- •Р озв’язування
- •Розв’язування
- •3.8 Основні операції векторного аналізу в криволінійних координатах
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 сПеЦіальні типи полів
- •4.1 Потенціальні векторні поля
- •Розв’язування
- •4.2 Соленоїдні (трубчасті) поля
- •Розв’язування
- •4.3 Гармонічне поле
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Література
- •Наталія Василівна Сачанюк-Кавецька Лідія Іванівна Педорченко Елементи теорії поля
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
Розв’язування
Знайдемо векторне
поле
![]() :
:
 .
Тобто
.
Тобто
![]() .
.
Знайдемо дивергенцію даного векторного поля. Оскільки
![]() ,
, ![]() ,
,
![]() ,
,
то
![]() ,
, ![]() ,
, ![]() .
.
Таким чином, дивергенція даного векторного поля за формулою (3.9) набуває такого вигляду:
![]()
Обчислимо дивергенцію векторного поля в заданих точках, маємо:
![]() ;
;
![]() ;
;
![]() .
.
Оскільки
![]() ,
а
,
а
![]() і
і
![]() ,
то в точці
,
то в точці
![]() векторне поле
векторне поле
![]() має стік, а в точках
має стік, а в точках
![]() і
і
![]() – джерела.
– джерела.
Приклад 3.2
Напруженість
![]() поля точкового електричного заряду
поля точкового електричного заряду
![]() на відстані
на відстані
![]() від цього заряду
від цього заряду
![]() ,
,
де
![]() – радіус-вектор, проведений з заряду
у довільну точку
– радіус-вектор, проведений з заряду
у довільну точку
![]() .
Визначити потік вектора
.
Визначити потік вектора
![]() через довільну замкнену поверхню, яка
не охоплює
заряд
через довільну замкнену поверхню, яка
не охоплює
заряд
![]() .
.
Розв’язування
Для обчислення
потоку вектора
![]() через довільну замкнену поверхню, яка
не охоплює заряд
через довільну замкнену поверхню, яка
не охоплює заряд
![]() ,
скористаємось формулою Остроградського-Гаусса,
записаною з використанням поняття
дивергенції векторного поля. Маємо:
,
скористаємось формулою Остроградського-Гаусса,
записаною з використанням поняття
дивергенції векторного поля. Маємо:
![]() .
.
Вважатимемо, що
заряд
![]() розмішений у початку координат, а точка
розмішений у початку координат, а точка
![]() має координати
має координати
![]() та
та
![]() .
Тоді радіус-вектор
.
Тоді радіус-вектор
![]() ,
а його модуль
,
а його модуль
![]() .
.
Тому рівність
![]() набуває вигляду:
набуває вигляду:
![]() ,
,
а
![]() ,
, ![]() ,
, ![]() .
.
Знайдемо тепер
![]() ,
,
![]() та
та
![]() .
.
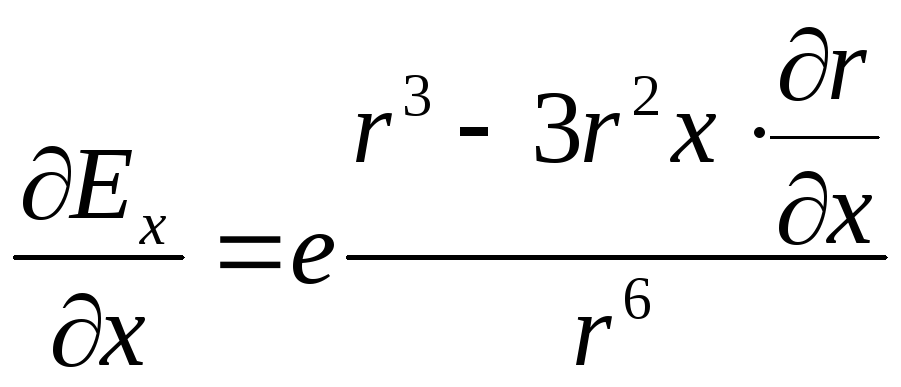 ,
,
але
![]() ,
а
,
а
![]() .
.
Тому
 .
.
Аналогічно
![]() ,
, ![]() .
.
Таким чином,
дивергенція векторного поля
![]() така:
така:
![]() .
.
П=![]() .
.
3.3 Проекція ротора векторного поля на вектор нормалі та ротор векторного поля
Нехай задано
векторне поле
![]() .
Виберемо в просторі деякий плоский
замкнений контур
.
Виберемо в просторі деякий плоский
замкнений контур
![]() і позначимо через
і позначимо через
![]() – вектор нормалі до площини, в якій
лежить цей контур. Криволінійний
інтеграл
– вектор нормалі до площини, в якій
лежить цей контур. Криволінійний
інтеграл
![]() (3.10)
(3.10)
називається
циркуляцією
векторного поля
![]() уздовж
контура
уздовж
контура
![]() .
.
Позначимо
![]() площу поверхні, обмеженої контуром
площу поверхні, обмеженої контуром
![]() .
Виберемо
усередині отриманої плоскої фігури
довільну точку і шляхом неперервної
деформації будемо стягувати контур
.
Виберемо
усередині отриманої плоскої фігури
довільну точку і шляхом неперервної
деформації будемо стягувати контур
![]() в цю точку, не змінюючи напрям нормалі
в цю точку, не змінюючи напрям нормалі
![]() .
Тоді
.
Тоді
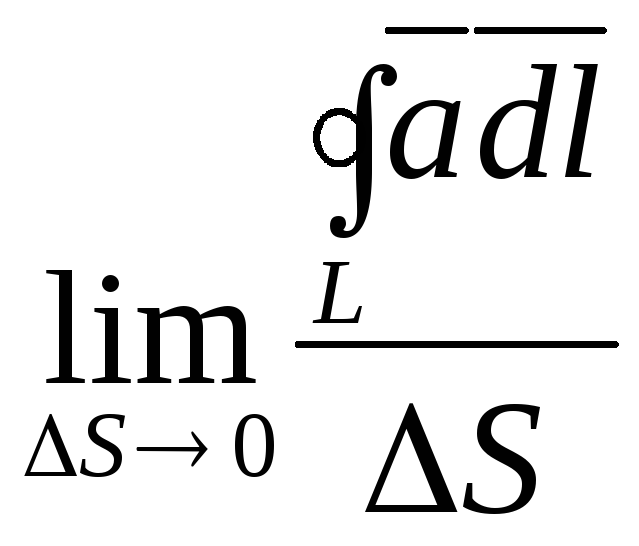 (3.11)
(3.11)
називається
проекцією ротора векторного поля в
точці
![]() у напрямі нормалі
у напрямі нормалі
![]() і позначається
і позначається
![]() ,
тобто:
,
тобто:
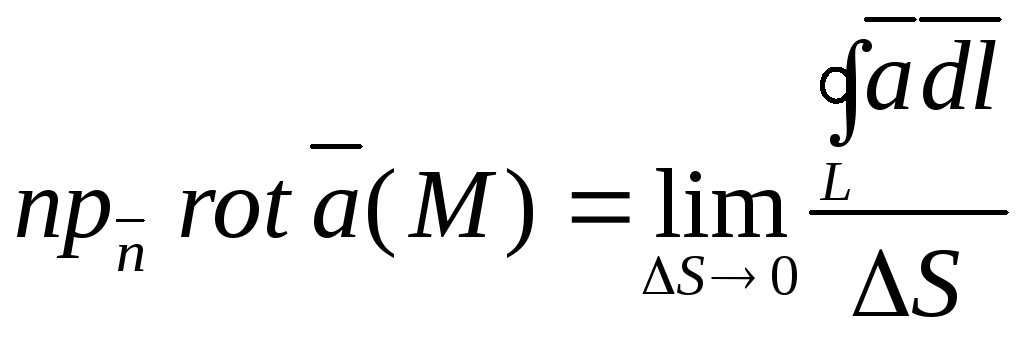 .
(3.12)
.
(3.12)
Загалом,
![]() характеризує густину циркуляції
векторного поля. У випадку поля швидкостей
рухомої рідини проекція ротора
векторного
поля в точці
характеризує густину циркуляції
векторного поля. У випадку поля швидкостей
рухомої рідини проекція ротора
векторного
поля в точці
![]() у напрямі нормалі характеризує
інтенсивність обертального руху.
Зокрема, якщо рух ламінарний, то
у напрямі нормалі характеризує
інтенсивність обертального руху.
Зокрема, якщо рух ламінарний, то
![]() у кожній точці дорівнює нулю. Вектор,
у напрямі якого
у кожній точці дорівнює нулю. Вектор,
у напрямі якого
![]() досягає максимального значення і модуль
якого дорівнює цьому максимальному
значенню, називають ротором
(вихором)
векторного поля і позначають
досягає максимального значення і модуль
якого дорівнює цьому максимальному
значенню, називають ротором
(вихором)
векторного поля і позначають
![]() .
.
Модуль та напрям ротора в загальному випадку змінюються при переході від однієї точки простору до іншої. Формула для обчислення ротора в декартових координатах має вигляд:
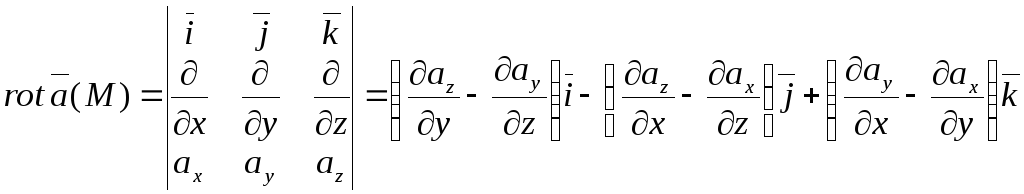 .(3.13)
.(3.13)
Приклад 3.3
Обчислити ротор векторного поля
![]() .
.
Розв’язування
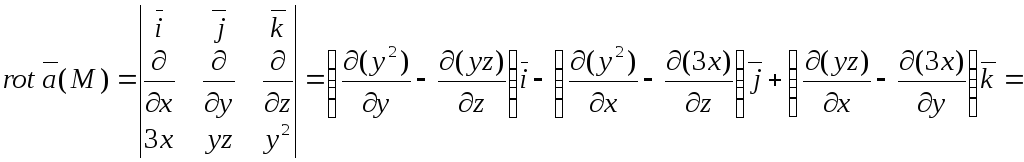
![]() .
Тобто
.
Тобто
![]() .
.
Приклад 3.4
Обчислити найбільшу густину циркуляції
векторного поля
![]() в точці
в точці
![]() .
.
