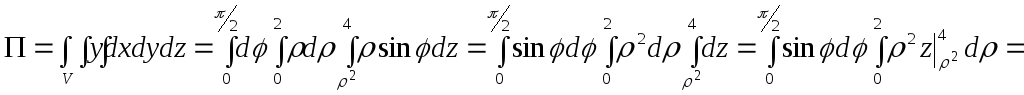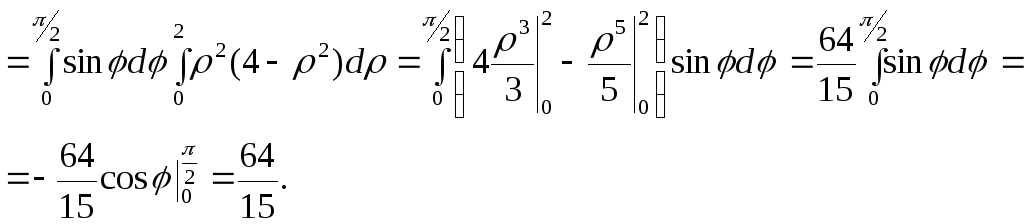- •Тема 1 скалярне поле та його характеристики 5
- •Тема 2 поняття векторного поля та його потоку 16
- •Тема 3 характеристики векторного поля 41
- •Тема 4 сПеЦіальні типи полів 79
- •Передмова
- •Тема 1 скалярне поле та його характеристики
- •1.1 Похідна за напрямом
- •Розв’язування
- •1.2 Поняття та властивості градієнта
- •Доведення
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 поняття векторного поля та його потоку
- •2.1 Потік векторного поля
- •2.2 Обчислення потоку векторного поля
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.3 Формула Остроградського-Гаусса
- •Розв’язування
- •Р озв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 характеристики векторного поля
- •3.1 Дивергенція (розбіжність) векторного поля
- •3.2 Обчислення дивергенції векторного поля в декартовій системі координат
- •Розв’язування
- •Розв’язування
- •3.3 Проекція ротора векторного поля на вектор нормалі та ротор векторного поля
- •Розв’язування
- •Розв’язування
- •3.4. Оператор Гамільтона
- •Розв’язування
- •3.5 Диференціальні операції другого порядку
- •Розв’язування
- •3.6 Властивості ротора векторного поля
- •Розв’язування
- •3.7 Циркуляція векторного поля та її обчислення. Формула Стокса
- •Розв’язування
- •Розв’язування
- •Р озв’язування
- •Розв’язування
- •3.8 Основні операції векторного аналізу в криволінійних координатах
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 сПеЦіальні типи полів
- •4.1 Потенціальні векторні поля
- •Розв’язування
- •4.2 Соленоїдні (трубчасті) поля
- •Розв’язування
- •4.3 Гармонічне поле
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Література
- •Наталія Василівна Сачанюк-Кавецька Лідія Іванівна Педорченко Елементи теорії поля
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
Розв’язування
Зробимо схематичний рисунок (рис. 2.8).
Р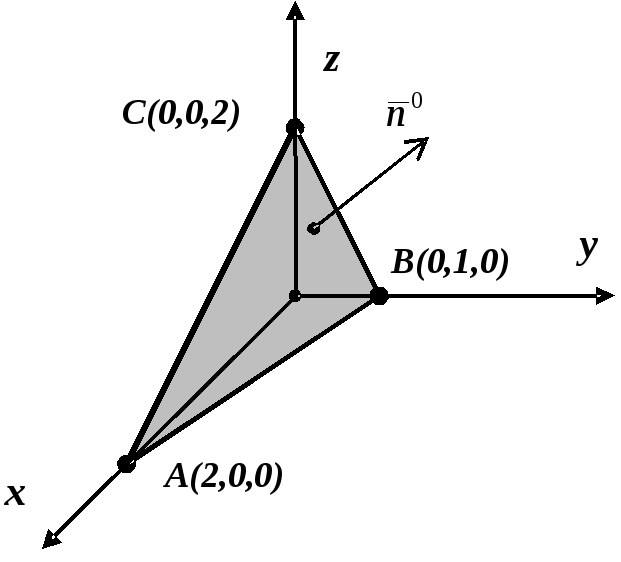 исунок
2.8
исунок
2.8
1. Обчислимо потік
векторного поля через верхню сторону
трикутника
![]() ,
утвореного при перерізі площини
,
утвореного при перерізі площини
![]() з координатними площинами (
з координатними площинами (![]() )
безпосередньо.
)
безпосередньо.
Оскільки поверхня
![]() взаємно однозначно проектується на
площину
взаємно однозначно проектується на
площину
![]() в область
в область
![]() ,
то обчислення потоку векторного поля
,
то обчислення потоку векторного поля
![]() через дану поверхню зводиться до
обчислення подвійного інтеграла по
області
через дану поверхню зводиться до
обчислення подвійного інтеграла по
області
![]() за формулою :
за формулою :
П1![]() . (2.26)
. (2.26)
За формулою (2.15)
знайдемо одиничний вектор нормалі до
поверхні
![]() .
Оскільки вектор
.
Оскільки вектор
![]() поставлений до зовнішньої сторони
поверхні, то у формулі (2.15) беремо знак
«плюс».
поставлений до зовнішньої сторони
поверхні, то у формулі (2.15) беремо знак
«плюс».
Обчислимо частинні
похідні функції
![]() за кожною змінною:
за кожною змінною:
![]() ,
, ![]() ,
, ![]() .
.
Тоді
![]() .
.
Обчислимо скалярний
добуток векторів
![]() та
та
![]() ,
заданих своїми декартовими координатами:
,
заданих своїми декартовими координатами:
![]() ,
,
тобто
![]() ,
при цьому
,
при цьому
![]() .
Тоді
.
Тоді
![]()
Отже,
![]()
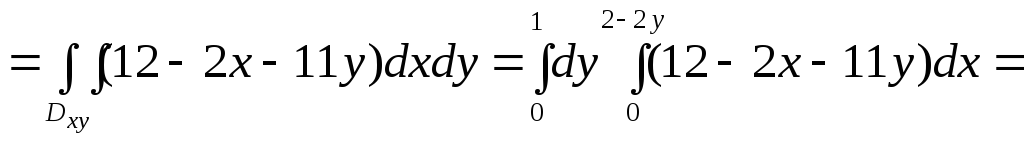
![]()
![]() ,
,
тобто П1=7 (рис. 2.9).
Р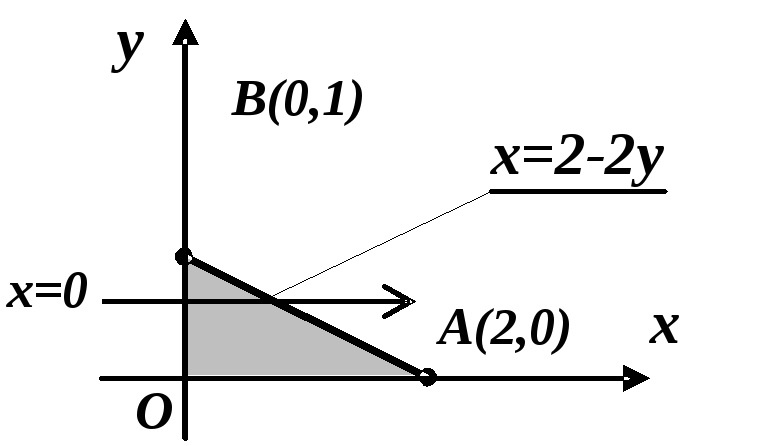 исунок
2.9
исунок
2.9
2. Обчислимо потік
векторного поля через повну поверхню
піраміди, утвореної площиною
![]() і координатними площинами, безпосередньо:
і координатними площинами, безпосередньо:
П=П1+П2+П3+П4,
де П1
– потік векторного поля через верхню
сторону трикутника
![]() ,
,
П2
– потік векторного поля через зовнішню
сторону площини трикутника
![]() ,
,
П3
– потік векторного поля через зовнішню
сторону площини трикутника
![]() ,
,
П4
– потік векторного поля через зовнішню
сторону площини трикутника
![]() .
.
Обчислимо П2
– потік векторного поля через зовнішню
сторону площини трикутника
![]() .
Рівняння площини
.
Рівняння площини
![]() :
:
![]() ,
одиничний вектор нормалі
,
одиничний вектор нормалі
![]() до цієї площини паралельний осі
до цієї площини паралельний осі
![]() ,
але має напрям, протилежний напряму
вектора
,
але має напрям, протилежний напряму
вектора
![]() .
Тому за умовою колінеарності векторів
.
Тому за умовою колінеарності векторів
![]() .
Тоді
.
Тоді
П2![]() ,
,
причому
![]() =-1,
=-1,
![]()
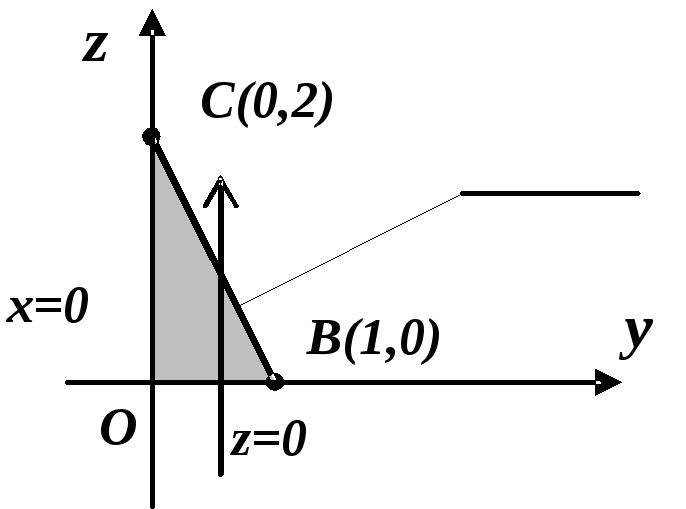 Маємо
(рис. 2.10):
Маємо
(рис. 2.10):
Рисунок 2.10

![]() .
Тобто П2
.
Тобто П2![]() .
.
Обчислимо П3
– потік векторного поля через зовнішню
сторону площини трикутника
![]() .
Рівняння площини
.
Рівняння площини
![]() :
:![]() ,
одиничний вектор нормалі
,
одиничний вектор нормалі
![]() до цієї площини паралельний осі
до цієї площини паралельний осі
![]() ,
але має напрям, протилежний напряму
вектора
,
але має напрям, протилежний напряму
вектора
![]() ,
тому
,
тому
![]() Тоді
Тоді
П3![]() ,
,
причому
![]() =-1,
=-1,
![]()
М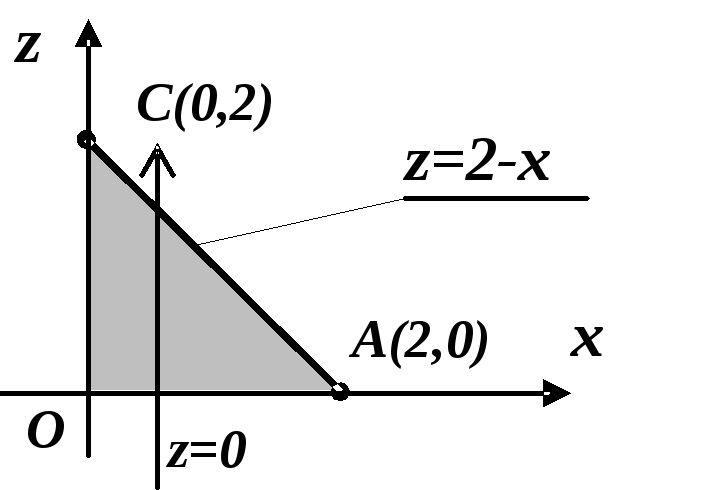 аємо
(рис. 2.11):
аємо
(рис. 2.11):
Рисунок 2.11
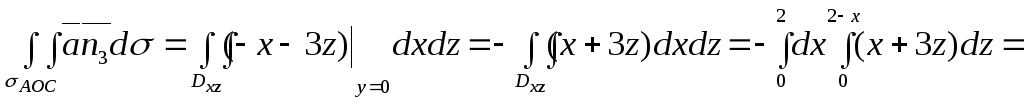
![]()
![]() тобто П3
тобто П3![]() .
.
Обчислимо П4
– потік векторного поля через зовнішню
сторону площини трикутника
![]() .
Рівняння цієї площини:
.
Рівняння цієї площини:
![]() ,
одиничний вектор нормалі
,
одиничний вектор нормалі
![]() до цієї площини паралельний осі
до цієї площини паралельний осі
![]() ,
але має напрям, протилежний напряму
вектора
,
але має напрям, протилежний напряму
вектора
![]() ,
тому
,
тому
![]()
Оскільки
![]() ,
то
,
то
П4![]() .
.
Таким чином, П![]()
3. Обчислимо потік векторного поля через повну поверхню піраміди в напрямі її зовнішньої нормалі за формулою Остроградського-Гаусса.
Обчислимо спочатку
вираз
![]() ,
маємо:
,
маємо:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
П=![]() .
.
Приклад 2.5
Обчислити потік вектора
![]() через зовнішню сторону поверхні
через зовнішню сторону поверхні
![]() ,
визначеної нерівностями
,
визначеної нерівностями
![]()
![]() :
:
а) безпосередньо;
б) за формулою Остроградського-Гаусса.
Р озв’язування
а) Зобразимо вказану поверхню (рис. 2.12):
Рисунок 2.12
Згідно з рисунком (2.12) маємо:
П=П1+П2+П3+П4,
де П1
– потік векторного поля через зовнішню
сторону поверхні
![]() :
:
![]() ;
;
П2
– потік векторного поля через зовнішню
сторону площини
![]() ;
;
П3
– потік векторного поля через зовнішню
сторону площини
![]() ;
;
П4
– потік векторного поля через зовнішню
сторону площини
![]() .
.
Обчислимо П1
– потік векторного поля через зовнішню
сторону поверхні
![]() :
:
![]() :
:
П1![]() .
.
За формулою (2.15)
знайдемо одиничний вектор нормалі
![]() .
Обчислимо спочатку частинні похідні
функції
.
Обчислимо спочатку частинні похідні
функції
![]() .
Маємо:
.
Маємо:
![]() ,
, ![]() ,
, ![]() ,
,
звідки
![]() ,
,
![]() =
=![]() .
.
Обчислимо скалярний
добуток
![]() :
:

Обчислимо вираз
![]() :
:
![]() звідки
звідки
![]()
Тоді
П1![]() .
.
Для обчислення отриманого подвійного інтеграла перейдемо до полярних координат за допомогою перетворення:
![]() ,
, ![]() .
.
Рівняння кола
![]() ,
що є лінією перетину параболоїда
,
що є лінією перетину параболоїда
![]() з площиною
з площиною
![]() ,
в полярних координатах матиме вигляд:
,
в полярних координатах матиме вигляд:
![]() ,
звідки
,
звідки
![]() або
або
![]() .
Тоді
.
Тоді
![]() ,
,
![]() ,
,
![]() .
.
Враховуючи введені заміни, маємо:
П1=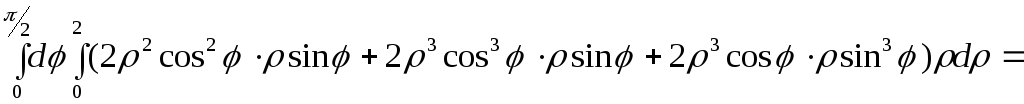
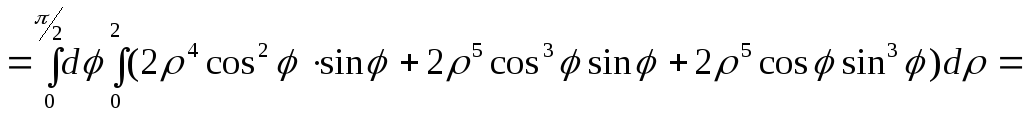
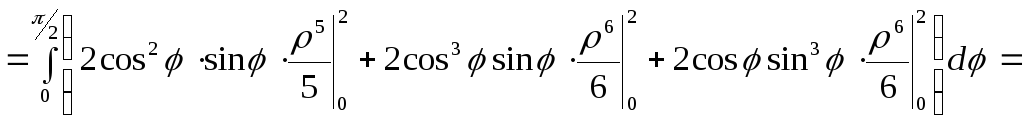
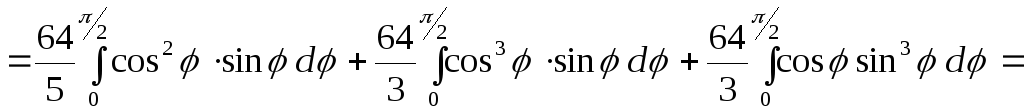
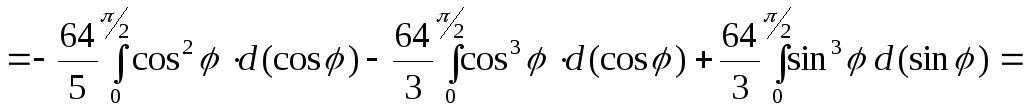
![]()
![]() ,
тобто П1=
,
тобто П1=![]() .
.
Обчислимо П2
– потік векторного поля через зовнішню
сторону площини
![]() :
:
![]() за формулою:
за формулою:
П2![]() ,
,
де одиничний вектор
нормалі
![]() паралельний осі
паралельний осі
![]() і колінеарний вектору
і колінеарний вектору
![]() ,
тому
,
тому
![]() .
.
Обчислимо скалярний
добуток
![]() :
:
![]() .
.
Отже,
П2![]() .
.
Обчислимо П3
– потік векторного поля через зовнішню
сторону площини
![]() :
:
![]() за формулою:
за формулою:
П3![]() ,
,
де
![]() – одиничний вектор нормалі до даної
поверхні, який паралельний осі
– одиничний вектор нормалі до даної
поверхні, який паралельний осі
![]() ,
але має напрям, протилежний напряму
вектора
,
але має напрям, протилежний напряму
вектора
![]() .
Тому
.
Тому
![]() ,
скалярний добуток векторів
,
скалярний добуток векторів
![]() дорівнює:
дорівнює:
![]() ,
а
,
а
![]() .
.
Тоді маємо
П3![]() .
.
Обчислимо П4
– потік векторного поля через зовнішню
сторону площини
![]() :
:
![]() за формулою
за формулою
П4![]() ,
,
де
![]() – одиничний вектор нормалі до даної
поверхні, який паралельний осі
– одиничний вектор нормалі до даної
поверхні, який паралельний осі
![]() ,
але має напрям, протилежний напряму
вектора
,
але має напрям, протилежний напряму
вектора
![]() ,
тобто
,
тобто
![]() .
.
Обчислимо скалярний
добуток векторів
![]() :
:
![]()
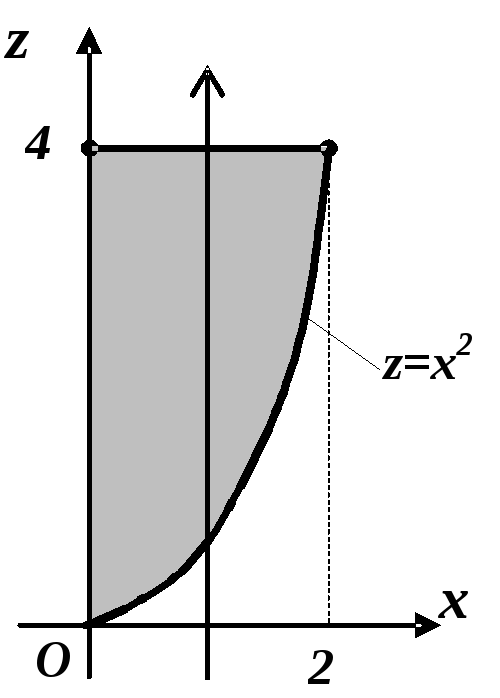 ,
,
![]() .
.
Тоді (рис. 2.13)
Рисунок 2.13
П4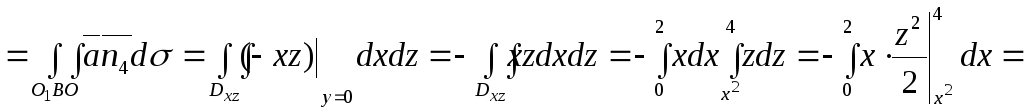
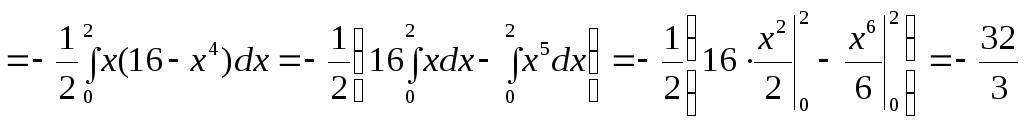 ,
,
тобто П4=![]() .
.
Таким чином,
П=П1+П2+П3+П4![]() .
.
б) Обчислимо потік
вектора
![]() через зовнішню сторону поверхні
через зовнішню сторону поверхні
![]() ,
визначеної нерівностями
,
визначеної нерівностями
![]()
![]() в напрямі її зовнішньої нормалі за
формулою Остроградського-Гаусса (2.17).
в напрямі її зовнішньої нормалі за
формулою Остроградського-Гаусса (2.17).
Обчислимо спочатку
вираз
![]() ,
маємо:
,
маємо:
![]() ,
,
![]()
![]()
![]() .
.
Таким чином, потік векторного поля обчислюється за формулою:
П![]() ,
,
де
![]() – область, обмежена параболоїдом
– область, обмежена параболоїдом
![]() ,
площиною
,
площиною
![]() і координатними площинами (рис. 2.12).
і координатними площинами (рис. 2.12).
Для обчислення одержаного потрійного інтеграла перейдемо до циліндричних координат за допомогою перетворення:
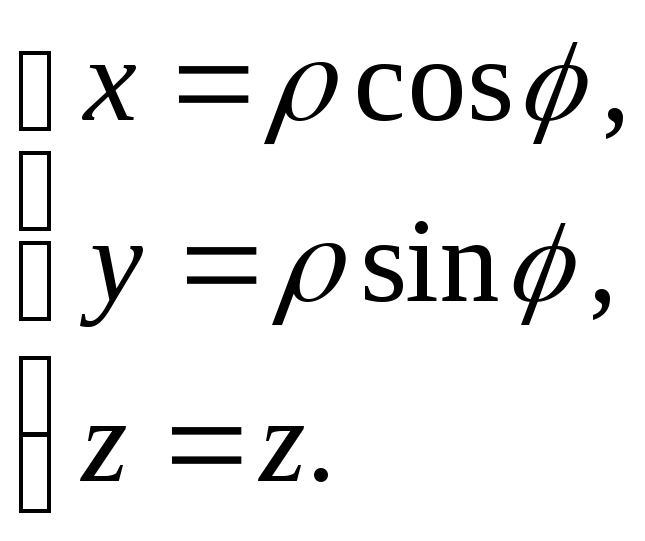
Рівняння поверхні
![]() в циліндричних координатах матиме
вигляд:
в циліндричних координатах матиме
вигляд:
![]() .
Тоді межі інтегрування будуть такі:
.
Тоді межі інтегрування будуть такі:
![]() ,
а
,
а
![]() .
.
Отже,