1. Формула 1.

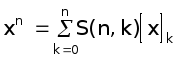(1.13)

Числа S(n, k) играют обратную роль по отношению к числам s(n, k) - позволяют перейти от базиса 1, x, x²,... к базису

Доказательство. Рассмотрим всевозможные отображения множества X из n элементов ( |X| = n) во множество Y из m элементов (|Y| = m). С одной стороны, по утверждению 1 .1 количество таких отображений есть mⁿ . С другой стороны, каждое такое отображение есть сюръективное отображение множества X на подмножество BY. Для произвольного подмножества B Y, где |B| = k  n число сюръективных функций f: XB в соответствии с утверждением 1 .12 равно k! S(n,k). Учитывая, что подмножество B мощности k можно выбрать способами получаем формулу:

(1.14)

Равенство ( 1 .14) можно рассматривать как равенство двух многочленов переменной x при всех целых положительных значениях x = m. Следовательно, эти многочлены тождественно равны между собой, так как их разность может быть либо тождественным нулем, либо должна иметь бесконечное число нулей, что невозможно. Справедливость формулы ( 1 .13) доказана. 

2. Формула 2.

Доказательство. Рассмотрим множество всех разбиений множества X={1, 2, ..., n+1} на m классов. Количество таких разбиений есть S(n+1, m). Все разбиения распадаются на различные типы, соответствующие разным подмножествам множества X, содержащим элемент n+1. Для каждого k- элементного подмножества B  X, содержащего элемент n+1, существует в точности S(n+1 k, m-1) разбиений множества X на m-1 класс, содержащих B в качестве класса. Действительно, каждое такое разбиение однозначно соответствует разбиению множества X \ B на m-1 класс. k - элементное подмножество B  X, содержащее элемент n+1 можно выбрать способами. Таким образом имеем:

3. Вернемся еще раз к связи комбинаторных объектов с исчислением конечных разностей. Из формулы ( 1 .13) следует, что, например,

, (1.15)

откуда заключаем на основании разложения ( 1 .8):

1! S(4, 1) = 1, 2! S(4, 2)=14, 3! S(4, 3) = 36, 4! S(4, 4) = 24.

Указанная связь дает альтернативный способ вычисления последовательности S(n, k). 

2. Числа Белла.

Определение.

Общее число разбиений множества X, |X| = n на произвольные классы называется числом Белла и обозначается B(n). Таким образом по определению:

.

Положим по определению B(0) = 1.

Формула 3.

.

Доказательство. Напомним, что S(n, m)= 0 при m>n.

Тогда имеем следующую последовательность очевидных равенств:

5. Принцип включений - исключений

Этот раздел посвящен важному комбинаторному методу - принципу включений-исключений, известному также под названиями: символический метод, принцип перекрестной классификации, метод решета. Логическое тождество, на котором основаны все эти методы, известны давно. Еще в 1713 году Монмор эффективно использовал упомянутый метод в решении знаменитой задачи о встречах (о числе перестановок из n элементов, в которых ни один элемент не сохраняет своей позиции).

Принцип включений - исключений - одно из фундаментальных средств перечислительной комбинаторики. Красота этого принципа лежит не в самом результате, а в его широкой применимости.

Принцип включений-исключений в перечислительной комбинаторике есть метод определения мощности множества S, который начинает с большего множества и каким-либо путем вычитает или аннулирует нежелательные элементы. Сначала дается приблизительный ответ, содержащий большее число элементов, затем вычитается число элементов, большее чем ошибка, полученная на первом шаге, пока мы не придем к правильному ответу. Это комбинаторная сущность принципа включения-исключения.

Для примера рассмотрим принцип включений- исключений в теоретико множественной форме.

Пусть даны два конечных множества A и B.

Тогда

AB= A + B  AB.

Чтобы вычислить количество элементов в объединении двух множеств, мы сначала вычисляем сумму их мощностей, но при этом дважды учитываем каждый элемент, принадлежащий пересечению множеств. Вычитая мощность пересечения, приходим к правильному ответу.

Совершенно аналогичные рассуждения позволяют выписать формулу для количества элементов в объединении трех множеств A, B, и C:

ABС= A + B +С  AB  AС  BC + ABC.

Вычитая дважды учтенные элементы попарных пересечений, мы трижды вычли элементы, принадлежащие пересечению всех трех множеств. Добавление мощности пересечения ABC приводит к нужному результату.

Пусть имеется N объектов и n различных свойств ___n. Каждый из объектов может обладать любым из этих свойств (в любом наборе), т.е. обладать любым набором этих свойств, или не обладать никаким из свойств.

Пусть N(₁) - число объектов обладающих свойством ₁. Некоторые из этих объектов могут обладать и другими свойствами в дополнение к ₁, но это неважно. (На самом деле в этом и состоит вся идея метода включений-исключений). Пусть теперь N(₂) - число объектов, обладающих свойством ₂ , и так далее. Соответственно, через N(₁, ₂) обозначим количество объектов, обладающих двумя свойствами: свойством ₁ и свойством ₂ .

В общем случае пусть N- число объектов, обладающих свойствами (и, быть может, некоторыми другими).

Пусть N₀ - число предметов, не обладающих ни одним из свойств __n.

Пусть - число объектов, не обладающих свойством ₁ . Чертой над символом свойства будем указывать, что речь идет об объектах, не обладающих таким свойством. Тогда в принятом обозначении N₀ = =.

Теорема 1.13. ( Формула включений - исключений).

. (1.16)

Прежде, чем переходить к доказательству, вернемся к ранее рассмотренному примеру с тремя множествами A, B, C. Пусть свойством ₁ обладают все элементы множества A, свойством ₂ обладают все элементы множества B, свойством ₃ - все элементы, принадлежащие множеству C. Тогда очевидно, что количество элементов, не обладающих ни одним из свойств ₁ , ₂ , ₃ , равно 0 (каждый элемент принадлежит хотя бы одному из множеств), и в соответствии с формулой ( 1 .16) имеем

Доказательство. Доказательство проводится индукцией по n - числу свойств. При одном свойстве  формула очевидна. Каждый объект либо обладает этим свойством, либо не обладает им. Поэтому N₀ = N  N().

Предположим теперь, что для случая, когда число свойств равно n1, формула доказана:

N₀ = N - N(_) - ... - N(_n-1) + N(__N_n-2, _n-1) + + (-1)^n-1 N(___n-1). (1.17)

Отметим очевидное соотношение:

(1.18)

Формула ( 1 .17) по предположению справедлива для любой совокупности объектов. В частности она верна для совокупности элементов, обладающих свойством _n. Применим индуктивное предположение к совокупности N(_n) для вычисления :

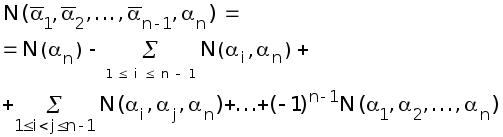(1.19)

Вычтем равенство ( 1 .19) из ( 1 .17). В правой части получим то, что нужно - правую часть формулы включения-исключения, а в левой части получим разность ( 1 .18). Тем самым формула ( 1 .16) доказана. 

Для того, чтобы облегчить всестороннее использование этой формулы, сделаем следующие замечания. Во-первых, лучше всего она запоминается в следующей “символической записи”:

Сначала вычисляется содержимое квадратных скобок, а затем знак функции N применяется к слагаемым:

NN

N[-



N[(

Далее, как видно из доказательства формулы включений - исключений, совокупности объектов, к которым применима теорема, не обязана быть совокупностью N всех объектов. Поэтому

___________

_______

Вообще, если n различных свойств __n объектов из совокупности N объектов обозначить , то

.

Рассмотрим принцип включений- исключений в несколько более общей форме. Пусть S - множество свойств, которыми элементы данного множества A могут обладать, а могут не обладать. Для любого подмножества T множества S, TS, пусть N₌(T) - число объектов множества A, которые обладают в точности свойствами из T (так что они не обладают никакими другими свойствами из ). Пусть N_(T) - число объектов множества A, обладающих по меньшей мере свойствами из T (и, возможно, какими-то другими свойствами). Ясно, что тогда

, (1.20)

, (1.21)

,

где Y пробегает все подмножества множества S.

В типичных приложениях принципа включений-исключений относительно легко вычислить N_ (Y) для YS, так что нами получена окончательная формула для N₌ (T).

Распространенным частным случаем принципа включения-исключения является выполнение условия N₌(T) = N₌(T^), как только T =  T^ . В рассматриваемом частном случае количество объектов, обладающих в точности заданным множеством свойств, зависит не от конкретного набора свойств, а только от числа рассматриваемых свойств. таким образом, N_(T) зависит также только от T  и мы полагаем

a(n  i) = N₌(T) (1.22)

и

b(n  i) = N_(T), (1.23)

если T = i.

Из формул ( 1 .20) и ( 1 .21) получаем, что формулы

, (1.24)

и

, (1.25)

эквивалентны. Это еще одно отражение комбинаторных соотношений взаимности.