1. Остовное дерево (каркас)

Для связного неориентированного графа G = < V, E > без петель каждое дерево < V, T > , содержащее все вершины графа G, где T  E, будем называть остовным деревом (каркасом) графа G.

Напомним, что длина пути есть количество составляющих его ребер.

Процедуры поиска в глубину и в ширину можно простым способом использовать для нахождения остовных деревьев. В обоих случаях достижение новой вершины u из вершины v вызывает включение в дерево ребра (v, u).

Приведем алгоритм построения остовного дерева методом поиска в глубину.

Алгоритм построения остовного дерева методом поиска в глубину.

Исходные данные: связный граф G =<V, E>, заданный списками инцидентности ЗАПИСЬ[v], vV.

Результат: каркас <V, T> графа G.

Алгоритм.

1 procedure КАРКАС_ГЛУБИНА(v)

{поиск в глубину из вершины v, соединенный с нахождением ребра дерева; переменные НОВЫЙ, ЗАПИСЬ, T - глобальные}

2 begin НОВЫЙ[v] := ложь;

3 for uЗАПИСЬ[v] do

4 if НОВЫЙ[u] then { (u, v) - новая ветвь}

5 begin T := T  (v, u); КАРКАС_ГЛУБИНА(u)

6 end

7 end {вершина v использована};

8 begin { главная программа}

9 for u  V do НОВЫЙ [u] := истина; { инициализация}

10 T := ;

{ T - множество найденных к этому времени ребер каркаса}

11 КАРКАС_ГЛУБИНА(r) {r - произвольная вершина графа }

12 end

Для доказательства того, что приведенный алгоритм правильно строит каркас произвольного связного графа, достаточно отметить следующие три факта. Во-первых, в момент добавления к множеству T нового ребра (v, u) в строке 5 в <V, T> существует путь из r в v (этот факт легко доказывается по индукции). Таким образом, алгоритм строит связный граф. Во-вторых, каждое новое ребро (v, u), добавляемое ко множеству T, соединяет уже рассмотренную вершину v (т.е. НОВЫЙ [v] = ложь ) с новой вершиной u. Отсюда следует, что построенный граф <V, T> не содержит циклов. Действительно, последнее ребро, “замыкающее” цикл, должно было бы соединить две уже рассмотренные вершины. И, наконец, в-третьих, из свойства поиска в глубину следует, что процедура КАРКАС_ГЛУБИНА просматривает все вершины связного графа. Следовательно, граф <V, T>, построенный нашим алгоритмом, есть остовное дерево графа G. Вычислительная сложность алгоритма есть, очевидно, O(n+m), т.е. того же порядка, что и сложность поиска в глубину.

Аналогично выглядит процедура построения остовного дерева методом поиска в ширину.

Алгоритм построения остовного дерева методом поиска в ширину.

Исходные данные: связный граф G =<V, E>, заданный списками инцидентности ЗАПИСЬ[v], vV.

Результат: каркас <V, T> графа G.

Алгоритм.

1 begin

2 for u  V do НОВЫЙ [u] := истина; { инициализация}

3 T := ; { T -множество найденных к этому времени ребер каркаса}

4 ОЧЕРЕДЬ := ; ОЧЕРЕДЬ  r;

5 НОВЫЙ [r] := ложь; { r - корень каркаса}

6 while ОЧЕРЕДЬ   do

7 begin p  ОЧЕРЕДЬ;

8 for u  ЗАПИСЬ [ v] do

9 if НОВЫЙ [ u] then

10 begin ОЧЕРЕДЬ  u; НОВЫЙ [ u ] := ложь;

T := T  (v, u);

11 end

12 end

11 end .

Рассуждениями, аналогичными проведенным для алгоритма КАРКАС _ ГЛУБИНА, можно показать, что данный алгоритм корректно строит остовное дерево для призвольного связного графа за O(n+m) шагов.

На следующем рисунке дан пример остовного дерева для графа, построенного методом поиска в ширину (а) и в глубину (б).

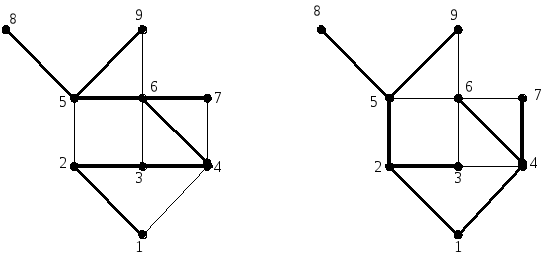
(а) (б)

Каждое остовное дерево, построенное с помощью метода поиска в глубину, имеет любопытное свойство, которое сейчас будет описано.

Вершину r, из которой начинается поиск, назовем корнем остовного дерева. Для двух различных вершин v и u дерева < V, T > будем говорить, что u является потомком вершины v, если v лежит на пути (в дереве < V, T >) из вершины u в вершину v.

Теорема 3.9.. Пусть < V, T > - остовное дерево связного графа неориентированного графа G = < V, E >, построенное с помощью алгоритма КАРКАС _ ГЛУБИНА, и пусть (u, v)  E. Тогда либо u - потомок v, либо v - потомок u.

Доказательство. Предположим без ограничения общности, что вершина v будет просмотрена раньше, чем u. Рассмотрим процесс поиска в глубину, начиная с вершины v. Очевидно, что по окончании его должно быть НОВЫЙ [u] = ложь, ибо (v, u) - ребро. Но это означает, что ребра, добавленные во множество T в течение этого процесса, содержат путь из v в u, откуда следует, что v лежит на пути из u в корень, поскольку в дереве существует в точности один путь из произвольной вершины к корню.

Рассуждения, проведенные в предыдущем разделе, непосредственно приводят к следующей теореме.

Теорема 3.10. Пусть < V, T > - остовное дерево связного графа неориентированного графа G = < V, E >, построенное с помощью алгоритма поиска в ширину. Тогда путь в < V, T > из произвольной вершины v до корня r является кратчайшим путем из v в r в графе G.

Далее особо обсуждается более общая задача отыскания кратчайших путей в графе, ребрам которого приписаны “длины” (веса), не обязательно равные единице.