2. Биномиальные коэффициенты

Cвое название биномиальные коэффициенты получили от соответствующей им производящей функции, являющейся степенью бинома:

(1.1)

Для доказательства справедливости написанного соотношения ( 1 .1) достаточно заметить, что коэффициент при x^k равен числу способов, которыми из m сомножителей (1+x) ... (1+x) можно выбрать k сомножителей.

Отметим некоторые важнейшие соотношения для биномиальных коэффициентов (чисел сочетаний).

1.

(1.2)

Это важнейшее соотношение - прямое следствие того факта, что каждому k-элементному подмножеству YX однозначно соответствует (n-k) - элементное подмножество X\Y множества X.

2.

(1.3)

Зафиксируем некоторый элемент x из n- элементного множества X. Множество T всех k - элементных подмножеств множества X распадается на два непересекающихся класса:

,

класс T₁ подмножеств, которые не содержат элемент x, и класс T₂ подмножеств, которые его содержат. Мощность первого класса составляет , а второго , то есть столько, сколько имеется (k-1) - элементных подмножеств множества X\{x}. 

Продемонстрируем эффективность использования производящей функции биномиальных коэффициентов для получения комбинаторных соотношений, включающих число сочетаний.

3. Полагая в ( 1 .1) x=1 получим

Эта формула следует и из того, что сумма слева есть число всех подмножеств n-элементного множества.

4.

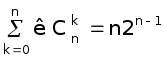(1.4)

Дифференцируя ( 1 .1) и полагая x=1, получаем соотношение ( 1 .4) .

5.

(1.5)

Равенство легко следует из следующего равенства для производящих функций:

(1+x)^m+n =(1+x)^m (1+x)ⁿ .

Полагая в ( 1 .5) m = k = n, получим

.

Отметим, что задача прямого доказательства последнего равенства без использования производящей функции достаточно трудна.

6. Полагая в ( 1 .1) x = –1, получаем

.

Отсюда следует, что

,

где через обозначена целая часть числа m/2. 

3. Исчисление конечных разностей

Приведем пример использования биномиальных коэффициентов в вычислительной математике.

Пусть дана функция , определенная на множестве действительных (возможно целых) чисел и принимающая действительные значения. Определим новую функцию (x), называемую первой разностью , формулой

.

Оператор  называется разностным оператором первого порядка; кратко и очень упрощенно можно определить исчисление конечных разностей как исследование оператора  . Можно применить оператор  k раз и получить k-ый разностный оператор

.

Число ^k(x) называется k-ой разностью  в точке x (^k(0) называется k-ой разностью  в 0).

Определим другой оператор E, называемый оператором сдвига, формулой

.

Таким образом, =E  I, где I означает единичный оператор:

.

Тогда первая разность функции может быть записана в виде:

.

Разности более высоких порядков определяются рекуррентным соотношением

Откуда получаем выражение для n -ой разности:

В частности,

, (1.6)

что дает явную формулу для k-ой разности в терминах значений (0), (1), ... , (k). Нетрудно обратить формулу ( 1 .6) и выразить (n) через ⁱ (0). Именно,

. (1.7)

Напишем теперь в строку значения

... (-2) (-1) (0) (1) (2) (3)...

Если внизу написать между каждой парой последовательных членов (i), (i +1) их разность (i +1)  (i) = (i), то получим последовательность

...(-2) (-1) (0) (1) (2) ... .

Повторение этой процедуры приводит к таблице разностей функции , k-ая строка которой состоит из значений ^k(n). Диагональ, начинающаяся в (0) и идущая направо вниз, состоит из разностей ^k (0) в 0. Например, пусть (n) = n⁴ . Таблица разностей (начинающаяся с (0) ) выглядит так:

0		1		16		81		256		625	...
	1		15		65		175		369
		14		50		110		194
			36		60		84
				24		24
					0

Из формулы ( 1 .7) следует, что

(1.8)

В этом случае, так как n⁴ - многочлен четвертой степени и при фиксированном k есть многочлен степени k, написанное выше разложение обрывается после члена , то есть ^k 0⁴ = 0, если k > 4 (или, более общим образом, ^k n⁴ = 0, если k > 4).

Предыдущее рассуждение, конечно, не относится лишь к функции n⁴ . Подобные рассуждения приводят к следующим результатам.

1. Функция  - полином степени, не превосходящей d, тогда и только тогда. когда ^d+1(n) =0 (или ^d(n) - постоянная).

2. Если многочлен (n) степени, не превосходящей d, разложен в ряд по базису , 0  k  d, то коэффициенты разложения есть ^k (0), то есть

. 

Еще одна связь комбинаторных объектов с исчислением конечных разностей дается формулой ( 1 .15).