5. Полиномиальные коэффициенты

Утверждение 1.9. Пусть X множество n различных объектов и пусть n₁, n₂,..., n_p неотрицательные целые числа, удовлетворяющие условию n₁+ n₂ + ... +n_p = n; количество размещений n объектов по ячейкам Y₁,...,Y_p, при которых каждая ячейка содержит n₁, n₂, ..., n_p объектов соответственно, есть

Доказательство. Пусть n₁ + n₂ + ...+ n_p = n. Ящик Y₁ можно наполнить различными способами, после чего ящик Y₂ можно наполнить способами и так далее.

Следовательно, искомое число размещений равно

=



Утверждение 1.10. Производящая функция для полиномиальных коэффициентов имеет следующий вид:

(1.10)

Доказательство. Для доказательства справедливости равенства ( 1 .10) достаточно заметить, что коэффициент при равен числу способов выбрать из n сомножителей n₁ сомножителей, из которых в произведение войдет переменная x₁ , n₂ сомножителей, из которых в произведение войдет переменная x₂ , и так далее. 

Следствие 1.

(1.11)

Для доказательства следствия 1 достаточно заметить, что

.

Отсюда следует равенство коэффициентов при соответствующих степенях в левой и правой частях последнего равенства:

Следствие 2.

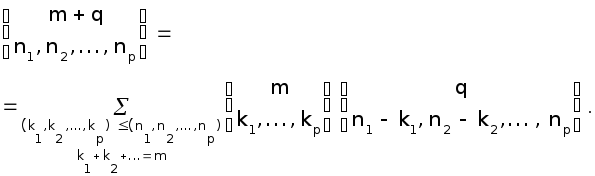
Указанное равенство есть непосредственное следствие следующего соотношения для производящих функций:

.

Следствие 3.

.

Равенство следствия 3 непосредственно вытекает из вида производящей функции для полиномиальных коэффициентов, если в ( 1 .10) положить:

x₁ = x₃ = x₅ = ... = +1 ,

x₂ =x₄ = x₆ = ... = –1 . 

4. Разбиения

   1. Число разбиений

Определение.

Разбиение конечного множества X, X = n , есть неупорядоченный набор  = {B₁ , B₂ , ... , B_k } подмножеств множества X таких, что

1. B_i   для всех i от 1 до k;

2. B_i  B_j =  , если i  j

3. B₁  B₂  ... B_k = X.

Мы называем B_i классом (блоком) разбиения  и говорим, что  имеет k классов. Пусть S(n, k) - число разбиений n - множества на k классов.

S(n, k) называется также числом Стирлинга второго рода. 

Разбиения соответствуют размещениям n различных объектов по k одинаковым ящикам при условии, что каждый ящик не пуст.

Пример.

S (4, 2) =7. Действительно, четыре объекта {1, 2, 3, 4} можно следующим образом разбить на два класса:

{1}{2, 3, 4}; {3}{1, 2, 4}; {1, 2}{3, 4};

{2}{1, 3, 4}; {4}{1, 2, 3} {1, 3}{2, 4};

{1, 4}{2, 3}. 

Условимся полагать, что S(0,0) = 1.

Читатель должен убедиться, что для n  1 имеют место соотношения:

S(0, k) = 0 при k>0,

S(n, k) = 0 при k > n,

S(n, 0) = 0,

S(n, 1) = 1,

S(n,2) = 2^n-1  1,

S(n, n) =1,

S(n, n  1) = .

Утверждение 1.11. Числа Cтирлинга второго рода удовлетворяют следующему основному рекуррентному соотношению:

S(n+1, k) = S(n, k  1) + kS(n, k). (1.12)

Доказательство.

Рассмотрим таблицу разбиений n+1 объекта на k классов.

1) Для некоторых разбиений (n+1)-ый объект есть единственный элемент в классе. Число таких разбиений есть S(n, k  1).

2) Для других разбиений (n+1)-ый объект не является единственным элементом класса ни для какого класса. Следовательно, существует kS(n, k) таких разбиений, так как каждому разбиению множества {1, ... , n} на k классов соответствует в точности k разбиений, образованных добавлением элемента n+1 поочередно к каждому классу.

Таким образом, мы представили все разбиения n+1 элемента на k классов в виде объединения непересекающихся подмножеств разбиений двух перечисленных типов. Поэтому

S(n+1, k) = S(n, k  1) + kS(n, k).

Утверждение 1.12. Число сюръективных отображений множества X, |X| = n, на множество Y (|Y| = m) равно m!S(n, m).

Доказательство.

Каждое сюръективное отображение X = {1,2,...,n} на Y = {y₁,y₂,...,y_m} индуцирует разбиение X на m различных классов 1,2,..., m (в класс i попадают все такие x, что f(x) = y_i); наоборот, каждому разбиению X на m классов соответствует m! сюръективных отображений X на Y. Действительно, выражение m!S(n, m) дает число способов разбить X на m классов, а затем линейно упорядочить классы, скажем, (B₁ , B₂ , ... , B_m ). Свяжем последовательность (B₁ , B₂ , ... , B_m ) с сюръективной функцией f, определенной формулой f(i) = y_j , если iB_j . Это устанавливает требуемое соответствие между количеством сюръективных отображений и числом разбиений. 

Ниже приводится список некоторых основных формул для количества разбиений множества из n элементов на k классов - S(n,k).