Контрольные вопросы.

1. В чем сущность метода укрупнения интервалов и для чего он применяется?

2. Как производится сглаживание рядов динамики способом скользящей (подвижной) средней? В чем достоинства и недостатки этого метода?

3. В чем сущность метода аналитического выравнивания динамических рядов?

4. Как определяется тип уравнения тенденции динамики?

5. Охарактеризуйте технику выравнивания ряда динамики по прямой.

6. Что представляют собой сезонные колебания, в чем практическое значение их изучения?

7. Как исчисляются индексы сезонности?

8. Каким методом пользуются, если уровень явления проявляет тенденцию к росту или снижению? В чем его сущность?

9. Что такое экстраполяция рядов динамики?

10. Охарактеризуйте нахождение точечных и интервальных прогнозируемых значений методом перспективной экстраполяции.

Тема 9. Выборочное наблюдение.

9.1. Понятие выборочного наблюдения (ВН).

9.2. Ошибки выборочного наблюдения.

9.3. Виды выборки.

9.1. Понятие выборочного наблюдения.

Выборочным наблюдением называется такое наблюдение, при котором обследованию подвергается некоторая часть совокупности, а обобщающие показатели, характеризующие эту исследуемую совокупность, распространяются на всю совокупность в целом.

Проведение выборочного наблюдения обуславливается тремя причинами:

• Выборочное наблюдение обладает рядом преимуществ перед сплошным: позволяет значительно сэкономить силы, средства и время проведения обследования; при его проведении представляется возможность значительно расширить программу статистического наблюдения, сделать ее более детальной. К выборочному наблюдению статистики прибегают также, когда необходимо уточнить результаты сплошного наблюдения;

• Выборочное наблюдение целесообразно в тех случаях, когда проводиться контроль качества разрушающими методами. Например, испытание деталей (узлов) по прогнозам параметрам, в результате, которого устанавливаются предельные показатели прочности, а деталь разрушается;

• Выборочное наблюдение проводится, когда невозможно провести сплошное наблюдение по времени и объему.

Всю массу единиц изучаемого объекта называют генеральной совокупностью. Совокупность единиц, отобранных для выборочного наблюдения, называют выборочной совокупностью.

Введем следующие обозначения:

N – число единиц, входящих в генеральную совокупность;

n – число единиц, входящих в выборочную совокупность.

- генеральная средняя (средне значение признака в генеральной совокупности);

- выборочная средняя;

р – генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности);

w – выборочная доля (отношение число единиц, обладающих определенным признаком выборочной совокупности к общей численности выборочной совокупности);

q – доля единиц, не обладающих определенным признаком (является дополнением генеральной доли до единицы). Сумма р + q = 1.

генеральная дисперсия (дисперсия признака в генеральной совокупности);

S² – выборочная дисперсия того же признака;

S – среднее квадратическое отклонение в выборке.

Пример: Численность студентов обучающихся в одном потоке составляет 200 человек. Необходимо определить успеваемость студентов в этом потоке и долю студентов имеющих хорошие и отличные оценки, в порядке 20% выборки.

Таблица 32

Исходные данные

Оценка (балл)	Число студентов (чел.)
«Неудовлетворительно» 2	20
«Удовлетворительно» 3	90
«Хорошо» 4	60
«Отлично» 5	30

Определим по исходным данным генеральной совокупности средний балл студентов по формуле

Доля студентов, имеющих хорошие и отличные оценки составляют: р=(60+30)/200=0,45. Осуществим отбор студентов для выборочной совокупности в порядке 20 выборки.

Таблица 33

Расчетные данные

Оценка (балл)	Число студентов генеральной совокупности	Число студентов, отобранных в выборочную совокупности
Неудов. (2)	20	5
Удовл.(3)	90	15
Хорошо(4)	60	13
отлично(5)	30	7
Итого	200	40

По данным, отобранным в выборочной совокупности, определим выборочную и выборочную долю W

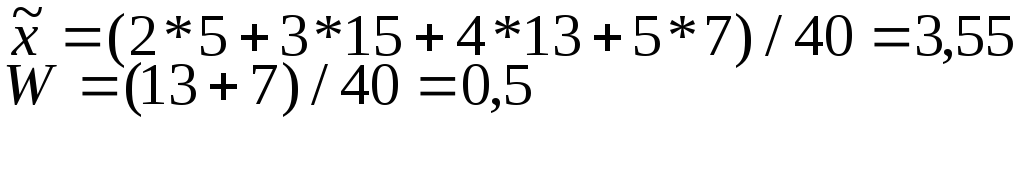
В результате в порядке 20% выборки мы получим те же самые показатели, что и при использовании данных генеральной совокупности.