6.3. Свойства дисперсии и способы ее исчисления.

Показатель дисперсии обладает рядом математических свойств, использование которых значительно упрощает ее исчисление.

Рассмотрим некоторые из этих свойств:

1. Если все значения признака уменьшить или увеличить на какое-то постоянное число, то дисперсия от этого не изменится.

2. Дисперсия постоянной величины равна нулю.

3. Если все значения признака уменьшить или увеличить в «А» раз, то дисперсия уменьшится или увеличится в «А» раз.

4. Сумма квадратов отклонений индивидуальных значений признака х от их средней величины меньше суммы квадратов отклонений индивидуальных значений признака от любого данного числа «а», при условии, что а ≠ , то есть

Способы расчета дисперсии:

1. Дисперсия есть средний квадрат отклонений индивидуальных значений признака от их средней величины: ;

2. Дисперсия есть разность между средней из квадратов значений признака и квадратом их средней:

где

Рассмотрим применение этих формул на примере. Распределение рабочих по тарифным разрядам:

Тарифный разряд 2 3 4 5 6

Число рабочих 1 2 6 8 3

Представим расчет дисперсии в табл. 19.

Таблица 19

Распределение рабочих по тарифному разряду

Тарифный разряд (х)	Число рабочих (f)
2 3 4 5 6 Итого	1 2 6 8 3 20	2 6 24 40 18 90	- 2,5 - 1,5 - 0,5 0,5 1,5 -	6,25 2,25 0,25 0,25 2,25 -	6,25 4,5 1,5 2 6,75 21,0	4 18 96 200 108 426

Средний тарифный разряд: разряда.

Дисперсия (1-й способ):

Дисперсия (2-й способ):

3. Для интервальных рядов распределения дисперсия может быть исчислена способом моментов:

где i – величина интервала;

m₁ – условный момент первого порядка;

m₂ – условный момент второго порядка.

где А – постоянная величина, от которой определяются отклонения (за нее обычно берут значение варианта (х) с наибольшей частотой (f).

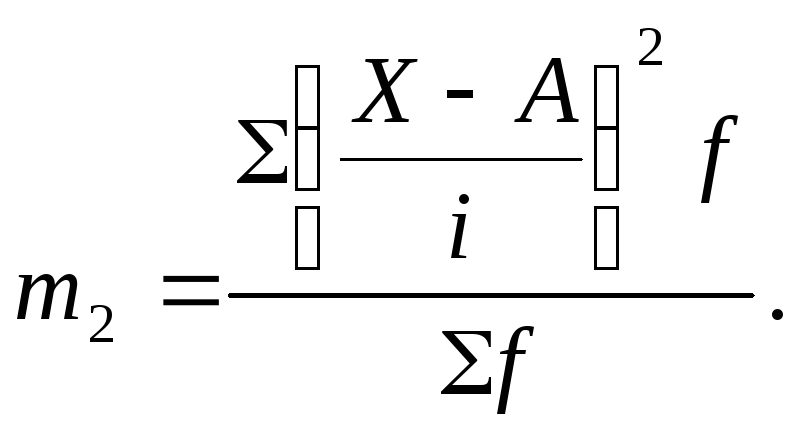
Для расчета средней величины способом моментов используют формулу:

Определим дисперсию способом моментов, представив условие и расчеты в табл. 20.

Таблица 20

Расчет дисперсии способом моментов

Межремонтный пробег автомобилей, тыс. км	Число автомобилей	х	х – А = = х - 130
80 – 100 100 – 120 120 – 140 140 - 160 Итого	5 30 50 15 100	90 110 130 150 -	- 40 - 20 0 + 20 -	- 2 - 1 0 + 1 -	- 10 - 30 0 + 15 - 25	4 1 0 1 -	20 30 0 15 65

4. При измерении вариации альтернативного признака дисперсию рассчитывают как:

где p – доля единиц совокупности, обладающих данным признаком;

q – доля единиц, не обладающих этим признаком.

Если обозначить наличие интересующего нас признака через «1», а его отсутствие через «0», то можно записать:

так как 1 – р = q.

Следовательно, дисперсия альтернативного признака равна произведению доли единиц, обладающих изучаемым признаком, на долю единиц, им не обладающих.

Например, если известно из 100 обследованных деталей 5 деталей оказались бракованными, то дисперсия альтернативного признака (наличие брака) составит: σ² = 0,05 х 0,95= = 0,0475.

Следует отметить, что при исчислении дисперсии в интервальных рядах распределения действительные значения признака заменяются центральными значениями интервалов. Это приводит к появлению систематической погрешности в расчете дисперсии. Поэтому возможно исчисление скорректированной дисперсии

Такая поправка применяется, если: 1) распределение относится к признаку с непрерывным характером распределения; 2) построено по большому количеству исходных данных (n > 500).