§ 35. О построении доверительных интервалов

Как мы уже отмечали в § 19, оценка с помощью доверительных интервалов является более совершенным способом, чем точечная оценка. При уравнивании геодезических сетей строят доверительные интервалы для истинных значений уравниваемых величин, их функций и для дисперсий (или средних квадратаческих отклонений) результатов измерений и их функций. Напомним, что доверительные интервалы имеет смысл строить, если измерения подчиняются нормальному закону распределения и не содержат систематических ошибок (кроме того случая, когда последние входят в уравнивание как неизвестные).

Доверительный интервал для истинного значения F любой функции F уравненных измерений строят в виде

(3.78)

где коэффициент выбирают из таблиц распределения Стьюдента по доверительной вероятности β и числу степеней свободы r = n - k, а средняя квадратическая ошибка

В частном случае для истинного значения X_j уравненного параметрическим способом неизвестного будем иметь интервал

Где

Так, в задаче 3.48 для уравненных отметок узловых точек нивелирной сети получим доверительные интервалы, построенные с вероятностью 0,95 (коэффициент t₃ при r = 4 равен 3,2)

189,614 - 3,21,7510^-2< Х₁< 189,614 + 3,21,7510^-2;

197,958 - 3,21,4810^-2 < Х₂ < 197,958 + 3,21,7510^-2;

190,981 -3,21,70 <Х₃< 190,981 +3,21,7010^-2

189,558 <Х₁< 189,670;

197,911 <Х₂< 198,005;

190,927 <Х₃< 191,035.

Для истинных значений уравненных превышений Υ₁ и Υ₅ получены доверительные интервалы

6,053 < Υ₁< 6,165; - 7,032 < Υ₅ < - 6,922.

Иногда результат уравнивания записывают в виде х_j± m_xj , что при большом r соответствует доверительному интервалу при β 0,7.

Доверительный интервал для с. к. о. единицы веса строят в виде

(3.79)

причем коэффициенты

выбираются из таблиц распределения χ², как описано в § 19, но по числу степеней свободы r = n - k. Так, для с. к. о, σ₀ при β = 0,90 и r = 4 будем иметь χ₁² = 9,5, χ₂² = 0,71 и доверительный интервал для σ₀ в задаче 3.48

Для с. к. о. функции доверительный интервал будет

(3.80)

а для

Например, для в этой же задаче будем иметь доверительный интервал см

Иногда вместо построения доверительного интервала для σ₀ вычисляют «ошибку ошибки» и пишут интервал в виде (при достаточно большом r) , а также, где

3.55. Построить доверительные интервалы для истинных значений уравненных углов в задаче 3.50 и для их средних квадратаческих отклонений, приняв β = 0,90; β = 0,95; β = 0,99.

3.56. Построить доверительные интервалы для истинных координат пунктов D и С, для средних квадратаческих отклонений , и , для средних квадратаческих отклонений функций в задачах 3.37, 3.38, 3.50 (доверительная вероятность β = 0,95).

§ 36. Решение нормальных уравнений по методу квадратных корней. Об ошибках вычислении

Как мы уже знаем (см. § 29), метод Гаусса решения системы нормальных уравнений

(3.81)

сводится к представлению матрицы R в виде произведения R = Т₁T₂ (см. стр. 159).

При этом получаем две системы уравнений

Т₁y = - b; T₂Δ = у,

где у - преобразованный в схеме Гаусса вектор b. Искомый вектор получается в схеме Гаусса по приведенным ранее формулам. Метод квадратных корней заключается в представлении матрицы в виде произведения R = Т^ТТ, где матрица

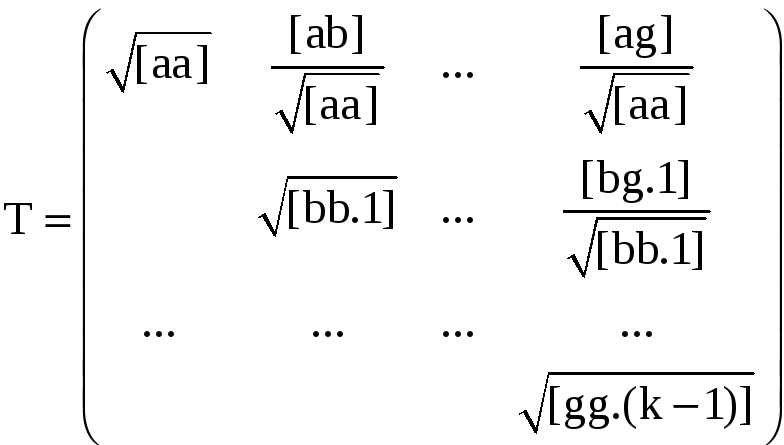
При этом вместо (3.81) имеем систему уравнений

(Ζ - преобразованный в схеме решения методом квадратных корней вектор b).

Вектор

Приведем схему решения системы нормальных уравнений вида Ах = b методом квадратных корней (признанным в настоящее время наиболее эффективным, так как он требует меньшей памяти ЭВМ) с попутным обращением матрицы А. Для трех неизвестных схема вычислений имеет вид табл. 92.

S = Ае + b - суммарный столбец, введенный для контроля (вектор е=(1 1 1)^т). Исходя из приведенных выше общих формул, связанных с решением системы нормальных уравнений методом квадратных корней, можно сформулировать следующие правила вычислений: элементы t_ij, z_i, вычисляют последовательно по строкам; t_ii — как корень квадратный из разности a_ii и суммы квадратов всех t_ij расположенных над t_ii недиагональный элемент t_ij получают вычитанием из а_ij , суммы

Таблица 92
Матрицы		Уравнения
		2,583	-1,167 2,833	-0,250 -1,000 1,887	1,684 -0,417 · -1,942	2,850 0,249 -1,305
		1,607 (0,6223) (0,6588) (0,8688)	-0,726 1,518	-0,156 -0,733 1,151	1,048 0,227 -1,400	1,774 1,013 -0,248
		0,336 1,337	-0,437 0,563	-1,216 -0,215
		-1,001	-1,000	-1,001
		0,551	0,311	0,238
		0,311	0,610	0,364
		0,238	0,364	0,755
Контроль		1,000	1,001	1,001

произведений элементов t, взятых из столбцов i и j, и умножением полученной разности на t_ii; аналогично вычисляют и элементы z_i

и s_i.

После вычисления всей строки производят контроль

(расхождения между Σ_i и ) допускаются в пределах нескольких единиц последнего удерживаемого знака). Неизвестные x_i определяют по формулам

Точно так же по столбцу s по мере получения x_i вычисляют величины и осуществляют контроль

Отметим, что при числе уравнений k < 10 в элементах t_ij удерживают на 1—2 знака после запятой больше, чем их имеют элементы a_ij, при 10 < k < 30 - на 3—4 знака больше.

Приведенная схема вычислений удобна и для обращения матрицы А. В самом деле, если решение системы уравнений Ах = b сводится к последовательному решению двух систем

то процесс обращения матрицы А, заключающийся в решении систем AQ_j = E_j (j = 1, 2, ..., k), где Q_j и Е_j - соответственно j - е столбцы матриц А и Е, может быть сведен к решению двух систем

(3.82)

(3.83)

Из системы (3.82) следует, что вектор

Учитывая правило обращения треугольной матрицы и введя матрицу , столбцами которой служат векторы , напишем

Здесь знаком вопроса обозначены неизвестные недиагональные элементы матрицы . Из системы (3.83) следует, что столбцы Q_j матрицы Q могут быть получены в схеме решения точно так же, как и вектор x, если столбец z последовательно заменить столбцами

, ,….

Элементы матрицы Q удобно вычислять по строкам, начиная с последней, как в способе Ганзена. При этом вычисленные элементы Q_ij i-й строки записывают в j-й столбец матрицы Q (в силу ее симметричности), так что в каждой строке необходимо вычислять элементы Q_ij при i > j (по этой причине обозначенные знаком вопроса неизвестные элементы матрицы вообще не участвуют в вычислениях).

После вычисления элементов каждой строки осуществляется контроль A_iQ_j 1, где A_i - i-я строка матрицы A(i = j).

Так, в рассмотренном примере весовые коэффициенты

Q₃₃ = 0.86882 = 0,755;

Q₃₂ = 0,7550,7330,6588 = 0,364;

Q₃₁ = (0,7550,156 + 0,3640,728)0,6223 = 0,238;

Q₂₂ = (0,6588 + 0,3640,733)0,6588 = 0,610;

Q₂₁ = (0,3640,156 + 0,6100,726)0,6223 = 0,311;

Q₁₁ = (0,6223 + 0,2380,156 + 0,3110,726)0,6223 = 0,551.

Контрольные вычисления получения каждой строки матрицы Q были показаны в § 30.

Метод квадратных корней, как и метод Гаусса, может применяться и для систем уравнений, в которых матрица А не положительно определена. Может оказаться, что < 0. В этом случае приходится прибегать к мнимым числам, что, однако, не вносит существенных затруднений.

3.57 Решить методом квадратных корней систему нормальных уравнений из задачи 3.48 с оценкой точности функций.Решение выполняем в табл. 93.

Таблица 93
Вспомогательные величины	Ьхх	**.	ь*ъ		S	Конт­роль 1	F,	F,	Ϊ	Конт­роль 2
	3,60	-1,17 4,88	- 1,22 -1,25 3,81	12,36 5,05 -16,37 121,26	13,57 7,51 - 15,03 122,30	13,57 7,51 -15,03 122,30	1,00 0 0	0 -1,00 -1,00	2,21 3.46 0,34
(0,5270) (0,4714) (0,5981)	1,897 -2,636 -3,636 1 0,376	-0,617 2,121 -0,855 - 1,855 1 0,132	-0,643 -0,776 1,672 3,172 2,172 1 0,164	6,514 4,275 -5,303 32,43 =Q	7,152 5,620 -3,631 32,44 32.44	7,151 5,620 -3,631 32,43	0,527 0,153 0,274 -0,376 -0,034	0 0,471 -0,380 +0,034 -0,36ο	1,165 1,970 1,566 -0,344 -0,332	1,165 1,970 1,566 -0,0342 -0,332
	0,132	0,270	0,131
	0,164	0,131	0,358

Заметим, что алгоритмы [pll.k], [pls.k] и [pss.k] и величины и вычисляют аналогично тому, как это делается в схеме Гаусса.

3.58 Решить методом квадратных корней системы нормальных уравнений из задачи 3.18.

3.59 Решить методом квадратных корней систему нормальных уравнений, возникающую в задаче 3.17

При решении систем нормальных уравнений неизбежны погрешности вычислений двух видов.

1. Погрешности из-за неизбежных округлений при вычислениях, поэтому вместо точных неизвестных x_j мы получаем . Подставив в исходную систему уравнений, вместо свободных членов b_j получим свободные члены

Если невязки превышают 1-2 единицы последних цифр свободных членов, то следует уточнить решение, приписав к схеме Гаусса дополнительно столбец . При этом точно так же, как описано выше, будут найдены поправки. Указанный процесс можно повторять неоднократно до тех пор, пока поправками, найденными на р - м шаге, можно будет пренебречь. Обычно при небольшом числе уравнений необходимость в указанных действиях отпадает

2.Погрешности, возникающие из-за ошибок в коэффициентах и свободных членах исходной системы, не могут быть устранены Однако можно вычислить погрешность получения неизвестных х_j. Допустим, что известны максимальные погрешности коэффициентов и свободных членов, которые мы обозначим через и ; тогда можно показать, что максимальное искажение свободных членов (максимальная «невязка») составит одинаковую в каждом уравнении величину

И тогда, приписав к системе уравнений столбец Δ, состоящий из единиц, и рассматривая его как столбец свободных членов b, получим неизвестные , …..

Эти величины вычисляются так же, как и , но так как знаки погрешностей и неизвестны, то, рассчитывая на самый неблагоприятный случай, мы должны оперировать только с модулями всех участвующих в вычислениях чисел. Таким образом (при k = 3),

;

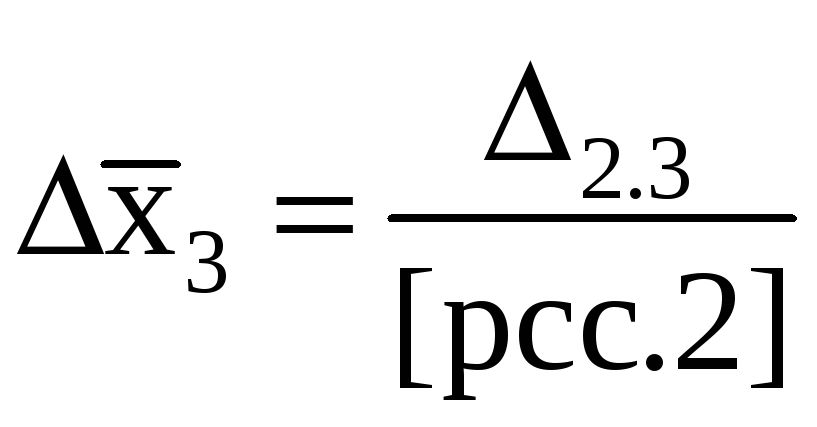Окончательно получаем неустранимые погрешности вычисления каждого неизвестного по формуле

На самом деле погрешности, конечно, значительно меньше.

Ниже приводится пример решения системы трех уравнений [8]:

4,15х₁ + 1,98 х₂ + 1,95 х₃ - 3,20 = 0;

1,98 х₁ + 3,02 х₂ + 0,99 х₃ - 2,60 = 0;

1,95 х₁ + 0,99 х₂ + 3,01 х₃ - 2,10 = 0

при Δα = Δb = 0,005.

Решение по схеме Гаусса дано в табл. 94

3.60 Самостоятельно выполнить решение по методу квадратных корней и сравнить погрешности вычислений в каждом методе.

Таблица 94
x1	x2	x3		s	Контроль
4,15 -1,000	1,98 -0,477	1,95 -0,470	-3,20 0,771	4,88 - 1,776	-1,776	0,241
	2,08 -1,000	0,06 -0,029	- 1,07 0,514	1,06 -0,510	1,07 -0,515	1,48 0,712
		2,09 - 1,000	-0,56 0,268	1,53 -0,732	1,53 -0,732	1,51 0,723
xj 0,404 -0,599 1,003	0,506 -0,489 0,995	0,268 -0,732 1,000
0,93 0,010	0,73 0,008	0,72 0,008