1.8. Сочетания с повторениями

Пусть задано 5 различных элементов a, b, c, d, e (в достаточном количестве комплектов) и пусть требуется составить из этих пяти элементов по 3 элемента сочетания с повторениями.

Это значит, что каждое соединение должно содержать три элемента и одно от другого должно отличаться, по крайней мере, одним элементом.

Если бы сочетания составлялись без повторений, то они должны были быть различными:

abc abd abe acd ace ade bcd bce bde cde.

Сочетания же с повторениями по три элемента из заданных пяти элементов будут иметь вид:

aaa aab aac aad aae abb abc abd abe acb acd ace add ade aee

bbb bbc bbd bbe bce bcd bce bdd bde bee

ccc ccd cce cdd cde cee ddd dde dee eee

Таким образом, сочетания же с повторениями из n элементов по m элементов (при 0≤ m ≤ n) может содержать любой элемент сколько угодно раз от до m включительно, или не содержать его совсем, т. е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но и из m каких угодно и как угодно повторяющихся элементов.

Следует отметить, что если два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.

Число сочетаний с повторениями из n элементов по m будем обозначать символом .

Существует формула для вычисления числа сочетаний с повторениями:

. (1.8.1)

Здесь m может быть и больше n.

Пример 1.8.1. В магазине продается видов тортов. Очередной покупатель выбил чек на три торта. Считая, что любой набор товаров равно-возможен, определить число возможных заказов.

Решение. Число равновозможных заказов по формуле (1.8.1) равно

Ответ: 220.

2. Решение задач

2.1. Разные задачи

Лучший способ освоения комбинаторики – решение задач. Начинать естественно, надо с простейших. Именно о простых, типовых (и в тоже время важнейших) задачах и пойдет речь.

Пример 2.1.1. В студенческой группе человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 20 человек, его заместителем – любой из оставшихся 19, а профоргом – любой из 18 студентов, т. е. n₁ = 20, n₂ = 19, n₃ = 18. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно

n₁ · n₂ · n₃ = 20 · 19 · 18 = 6 840 способов.

Ответ: 6 840.

Пример 2.1.2. Четыре юноши и четыре девушки садятся на 8 расположенных подряд стульев, причем юноши садятся на места с четными номерами, а девушки – на места с нечетными номерами. Сколькими способами это можно сделать?

Решение. Первый юноша может сесть на любое из четырех четных мест, второй – на любое из оставшихся трех мест, третий – на любое из оставшихся двух мест. Последнему юноше предоставляется всего одна возможность. Согласно правилу произведения, юноши могут занять четыре места 4 · 3 · 2 · 1 = 24 способами. Столько же возможностей имеют и девушки.

Таким образом, согласно правилу произведения, юноши и девушки могут занять все стулья 24 · 24 = 576 способами.

Ответ: 576.

Пример 2.1.3. В ящике 250 изделий. Известно, что 100 из них – первого, 120 – второго, а остальные – третьего сорта. Сколько способов выбора извлечения из ящика одной детали первого или третьего сорта?

Решение. Деталь первого сорта может быть извлечена n₁ = 100 способами, третьего сорта – n₂ = 30.

По правилу суммы существует n₁ + n₂ = 100 + 30 + 130 способов извлечения одной детали первого или третьего сорта.

Ответ: 130.

Пример 2.1.4. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?

Решение. Число разных способов распределения медалей равно

.

Ответ: 3 360.

Примечание. Необходимо различать сочетания и размещения. Например, в группе – 25 студентов, из них вышли из аудитории на перерыв. Студенты стоят вместе и беседуют. Тогда порядок, в котором они стоят, – не существенен. Число всех возможных групп из 25 человек по в этом случае – сочетания. Если же студенты отправились на перерыве в буфет или в кассу за стипендией, то тогда существенно, в каком порядке они стоят, т. е. кто из них первый, второй и т.д. В этой ситуации при подсчете возможных групп из 25 человек по необходимо составлять размещения.

Пример 2.1.5. У туриста есть семь консервных банок с ухой. В походе он будет находиться девять дней; из них какие-то семь дней будет есть уху, а три дня будет питаться всухомятку. Сколько у туриста есть способов выбрать дни с горячим питанием?

Решение. Число способов равно . Используя формулу (1.5.1), находим:

Ответ: 36.

Пример 2.1.6. В спортивной секции занимается баскетболистов. Сколько может быть организовано тренером разных спортивных пятерок?

Решение. Число разных спортивных пятерок равно . Используя формулу (1.5.1), находим:

.

Ответ: 792.

Пример 2.1.7. Из группы, состоящей из человек, выбирают троих для поездки на соревнование. Сколькими способами это может быть сделано?

Решение. Число способов равно . Используя формулу (1.5.1), находим:

.

Ответ: 2 300.

Пример 2.1.8. Для подарков ко дню 8 Марта молодой человек должен приобрести две броши и три браслета. В магазине ему предложили на выбор пять брошей и семь браслетов. Сколькими способами человек может сделать выбор?

Решение. Две броши из пяти можно выбрать числом способов, равным , а три браслета из семи – числом способов . Каждый из способов выбора броши нужно скомбинировать с каждым из способов выбора браслета. Следовательно, полное число способов, какими человек может выбрать две броши и три браслета, есть

.

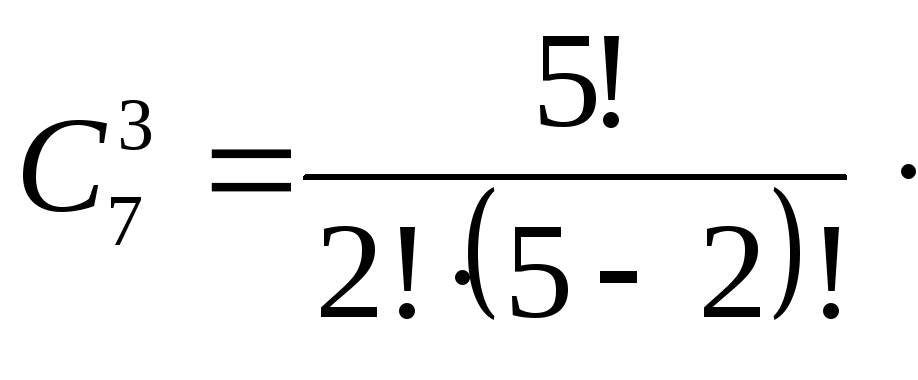
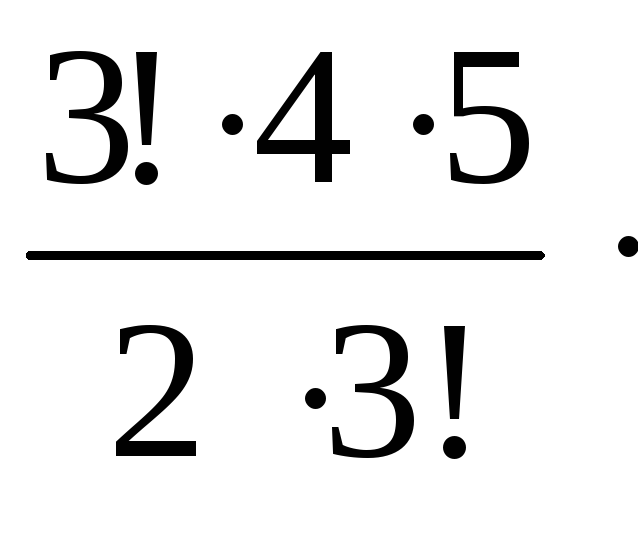
Ответ: 350.

Пример 2.1.9. Восемь человек должны расположиться в двух комнатах, причем так, чтобы в каждой было не менее трех человек. Сколькими способами это можно сделать?

Решение. Есть два варианта. Первый вариант: в одной комнате три человека, а в другой пять. Второй: в каждой комнате по четыре человека.

В первом варианте количество способов расположения восьми человек в двух комнатах равно числу сочетаний трех из восьми (или пяти из восьми, что одно и то же), во втором варианте – числу сочетаний четырех из восьми .

Полное число способов расположения восьми человек в двух комнатах должно учитывать как первый, так и второй варианты:

.

Ответ: 126.

Пример 2.1.10. Группу из девяти человек надо разбить на три подгруппы: в одной два человека, в другой три, в третьей четыре. Сколькими способами можно выполнить такое разбиение?

Решение. Сначала выясняем, сколькими способами можно выбрать двух человек из девяти. Это число способов равно . После того, как этот выбор состоялся, осталось семь человек. Из них надо организовать подгруппы из трех и четырех человек. Это можно сделать числом способов, равным (или , что одно и то же). Итак, девять человек можно разбить на два, три и четыре следующим числом способов:

.

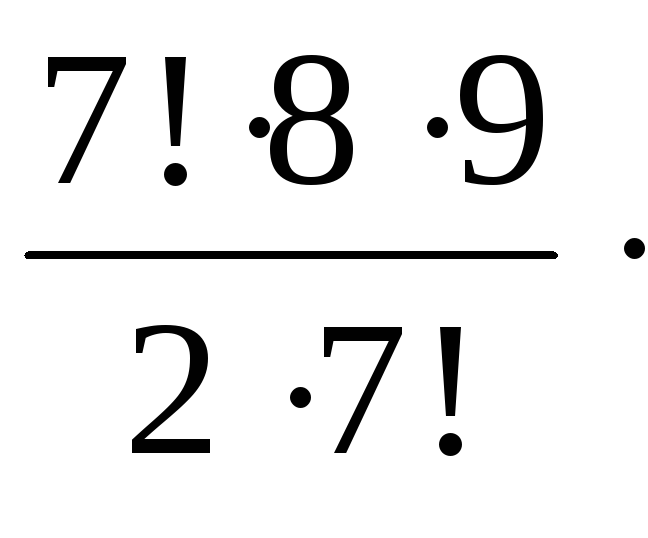
Примечание. Можно было бы сначала выяснить, сколькими способами можно выбрать трех человек из девяти. Тогда ответ на вопрос задачи дало бы произведение . А можно было бы сначала выяснить, сколько есть выборок четырех человек из девяти. Тогда ответ дало бы произведение . Докажите самостоятельно, что .

Ответ: 1260.

Пример 2.1.11. Сколькими способами можно из 40 человек, поступающих в вуз, создать 4 группы разных специальностей по 10 человек в каждой?

Решение. Первую группу можно создать способами. Вторую группу можно создать из оставшихся 30 человек способами. Третью группу можно создать из оставшихся 20 человек способами. Оставшиеся 10 человек составят четвертую группу. Итак, число всех различных способов составляет четырех групп из 40 человек равно

Ответ: .

Пример 2.1.12. Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй – не более девяти человек?

Решение. Первая подгруппа может состоять либо из трех, либо из четырех, либо из пяти человек. Подгруппу из трех человек можно выбрать способами. Подгруппу из четырех человек можно выбрать способами, а подгруппу из пяти человек – способами. Учитывая, что выбор первой подгруппы первой подгруппы однозначно определяет вторую, найдем по правилу суммы искомое число способов: .

Ответ: 1 507.

Пример 2.1.13. Сколькими способами можно рассадить за столом пять гостей, если стол накрыт на семь персон?

Решение. Пять гостей из семи можно выбрать способами. Но это не ответ на поставленный в задаче вопрос, поскольку при рассаживании гостей за столом необходимо принимать во внимание также число перестановок пяти гостей (оно равно P₅). Ведь занявших те или иные пять стульев можно поменять местами. Таким образом, пять гостей можно рассадить за столом, накрытым на семь персон, числом способов, равным

.

Ответ: 2 520.

Пример 2.1.14. Десять команд участвуют в розыгрыше первенства по футболу, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места, не будут участвовать в следующем первенстве.

Сколько различных вариантов результата первенства может быть, если учитывать только положение первых трех и последних двух команд?

Решение. Задачу решим тремя способами.

Способ 1. Первые три места могут быть распределены способов. В результате останется семь команд, две из которых выбывают из следующего первенства.

Так как в этом случае порядок выбывших команд не важен, то это может произойти способами. Согласно правилу умножения получаем, что число различных результатов первенства равно .

Способ 2. Выберем без учета порядка пять команд из общего числа команд. В эту группу входят три команды, занявшие призовые места, и две выбывшие команды. Такую операцию можно выполнить способами. Из этих пяти команд без учета порядка выделим две команды, которые выбывают, что можно сделать способами. Для оставшихся трех команд распределение призовых мест возможно P₃ способами. По правилу умножения все три операции можно выполнить P₃ = 15 120.

Способ 3. Распределение всех 10 мест в первенстве возможно P₁₀ = 10! способами.

Однако перестановки команд, занявших места с 4-го по 8-е, и перестановки команд, занявших 9-е и 10-е места, на результаты первенства не оказывают влияния. Число таких перестановок равно 5! · 2!, а число различных результатов первенства равно .

Ответ: 15 120.

Пример 2.1.15. Для освещения аудитории может быть включена каждая из имеющихся ламп. Сколько существует различных способов освещения аудитории?

Решение. Очевидно, что и число способов равно 2¹⁰ = 1 204. При этом учитывается и тот способ «освещения», при котором ни одна лампочка не горит.

Ответ: 1 024.

Пример 2.1.16. В кондитерском магазине продавались пирожные четырех видов: корзиночки, наполеоны, песочные и эклеры. Сколькими способами можно выбрать 7 пирожных?

Решение. В данной задаче подразумевается, что количество пирожных каждого сорта не ограничено. Для ответа на поставленный вопрос воспользуемся формулой сочетаний с повторениями (1.8.1):

.

Ответ: .

Пример 2.1.17. На конкурс представлено 10 студенческих работ. Денежные премии будут присуждаться по следующим номинациям: оригинальная научная идея; использование современного экономико-математи-ческого аппарата; применение компьютерного обеспечения; презентация результатов на научной конференции.

Сколько существует вариантов распределения премий, если по каждой комбинации установлены:

а) различные денежные премии;

б) одинаковые премии.

Решение

А. Каждый из вариантов распределения премий представляет собой комбинацию 4 работ из 10, отличающуюся от других комбинаций как самими работами, так и их порядком расположения по номинациям; причем одни и те же работы могут повторяться несколько раз, так как любая научная работа может получить премии как по одной, так и по нескольким (даже всем четырем) номинациям.

Число возможных вариантов распределения денежных премий представляет собой число размещений с повторениями из 10 элементов по 4 и определяется по формуле (1.8.1):

Б. Если по каждой номинации установлены одинаковые премии, то порядок следования работ в комбинации четырех премиальных работ значения не имеет. И тогда число вариантов распределения премий представляет собой число сочетаний с повторениями из 10 элементов по 4, определяемое по формуле (1.8.1):

Ответ: а) ; б) .