Лекція 3. Моделювання лінійних електричних кіл. Методи розв'язання систем лінійних рівнянь

Моделювання лінійних електричних кіл засновано на законах Кірхгофа (перший закон – слідство принципу безперервності електричного струму; другий – слідство закону збереження енергії) і Ома.

Метою розрахунку є визначення струмів у всіх гілках, напруг в вузлах, потужностей електроприймачів.

Математична модель електричного кола надається еквівалентною схемою що містить m гілок і n вузлів, а також ЕРС всіх джерел, внутрішніми і зовнішніми опорами.

Послідовність розрахунку лінійного електричного кола з використанням законів Кірхгофа наступна:

а) для кожної гілки вводять позначення протікаючого через неї струму і стрілками на схемі указують умовні позитивні напрями цих струмів;

б) для n-1 вузлів складають рівняння на підставі першого закону Кірхгофа; для одного з вузлів таке рівняння не складають, оскільки воно є слідством вже написаних рівнянь;

в) беруть взаємно незалежні контури кола (це означає, що в кожному новому контурі хоча б в одній з гілок струм не входить в попередньо розглянуті контури), в кожному з цих контурів вибирають умовний позитивний напрям обходу і позначають його на схемі;

г) для вибраних контурів складають рівняння по другому закону Кірхгофа з урахуванням напряму обходу; при правильному виборі контурів їх число повинно дорівнювати m - n + 1; при цьому загальна кількість рівнянь повинно складати m, тобто по числу невідомих величин;

д) вирішують отриману систему з m рівнянь одним з методів обчислювальної математики.

Якщо розраховане значення струму в даній гілці є позитивним, то це означає, що дійсний напрям струму співпадає з вибраним раніше і навпаки.

Складання системи лінійних рівнянь (СЛР) розглядається на прикладі схеми розгалуженого електричного кола постійного струму (рис.3.1). Параметри резисторів складають відповідно: ЕРС джерел, що містяться у гілках схеми:

Згідно законів Кірхгофа, алгоритму розрахунку, схеми електричного кола і напрямку обходу контурів система лінійних алгебраїчних рівнянь (СЛАР) має вигляд (3.1), де невідомі - це струми в гілках, коефіцієнти при невідомих – параметри елементів, а вільні члени – ЕРС джерел:

Рисунок 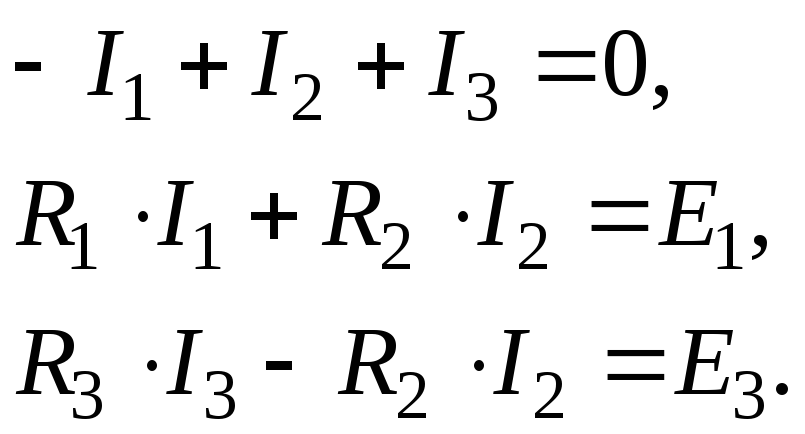3.1

(3.1)

Надалі, СЛАР, що отримано, розв'язується різними методами.

3.1 Форми запису систем лінійних алгебричних рівнянь і способи розв'язання матричних рівнянь

В загальному вигляді система n лінійних алгебричних рівнянь з n невідомими записується так:

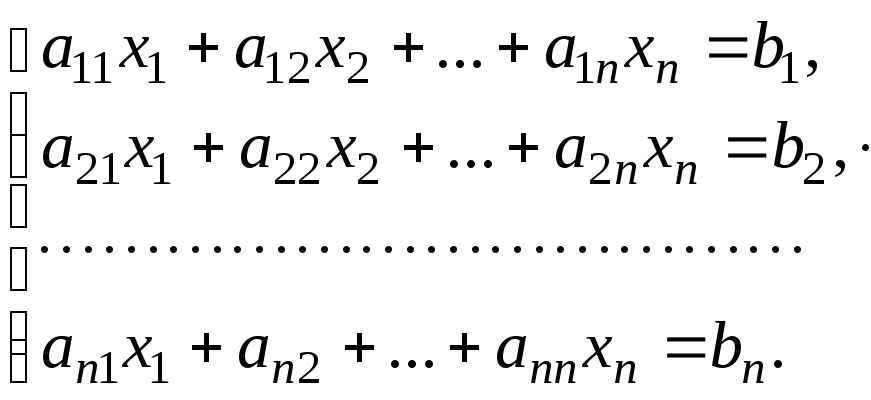(3.2)

Коротко систему (3.2) можна записати в такому вигляді:

(і = 1, 2, …, n). (3.3)

З використанням матричних позначень систему (3.2) можна записати в наступному виді:

, (3.4)

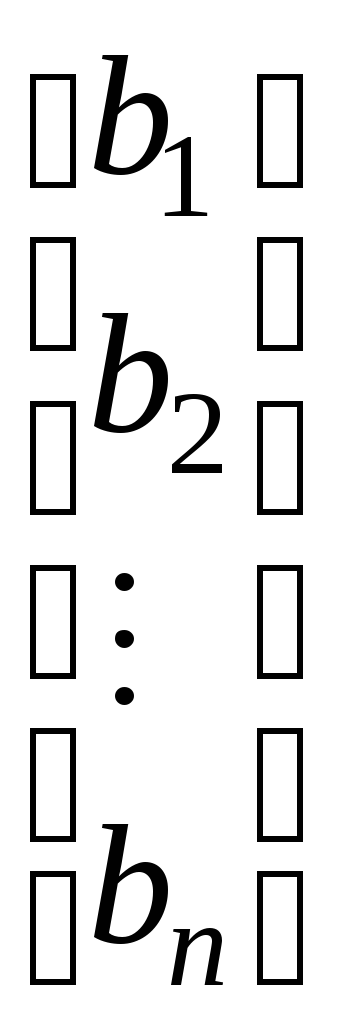
або в розгорнутому вигляді:

· = . (3.5)

Взагалі, розглядаються три види матричних рівнянь і способи їх розв'язання.

Матричне рівняння виду . Для розв'язання такого рівняння треба помножити зліва обидві його частини на обернену матрицю : . При цьому добуток (одинична матриця), отже, , звідки

. (3.6)

Матричне рівняння виду . Треба помножити справа обидві його частини на : . Виходить: , звідки

. (3.7)

Матричне рівняння виду . При помноженні обох частин рівняння – зліва на , а справа на виходить , або , звідки

. (3.8)

3.2 Методи розв'язування СЛАР

Методи поділяють на прямі, які використовують для обчислення невідомих кінцеві співвідношення (формули) і чисельні, які, в загальному випадку, поділяються на ітераційні методи і методи мінімізації.

Прямі методи дають розв'язок після виконання заздалегідь відомої кількості операцій. Ці методи прості і універсальні. Разом з тим їм властиві такі недоліки:

– вони потребують зберігання в оперативній пам'яті відразу всієї матриці;

– не враховують структуру матриці – нульові елементи також зберігаються в пам‘яті і над ними проводяться арифметичні дії;

– відбувається накопичення похибок в процесі розв'язування (хоч прямі методи і називають точними), тому що обчислення на будь-якому етапі використовують результати попередніх операцій.

У зв‘язку з цим прямі методи використовують для порівняно невеликих (n < 200) систем із щільно заповненою матрицею і не близьким до нуля визначником.

Чисельні методи, як ітераційні, так і мінімізації – це методи послідовних наближень. Вони потребують деякого наближеного розв'язку – початкового наближення. Далі за визначеним алгоритмом виконується ряд ітерацій до одержання результату з необхідною точністю. Методи мають перевагу перед прямими в наступному:

– потребують зберігання не всієї матриці системи, а лише декількох векторів з n компонент; іноді елементи матриці можна зовсім не зберігати, а обчислювати їх при необхідності;

– похибки кінцевих результатів не накопичуються, тому що в кожній ітерації використовується результат тільки попередньої і не використовуються раніше виконані обчислення.

Але при цих перевагах збіжність ітераційних методів може бути дуже повільною.

3.2.1 Прямі методи розв'язування СЛАР

Прямі методи розглядаються у вузівському курсі «Вища математика» і в даному курсі про них тільки згадується.

Отже, перший з прямих методів – це метод, що використовує формули Крамера, де невідомі визначаються як відношення визначників.

Найбільш поширеним прямим методом розв‘язання СЛАР на ЕОМ є метод послідовного виключення невідомих (метод Гаусса) і його модифікації.

Один з різновидів методу Гаусса (компактна схема Гаусса) – метод LU–перетворення.

Компактні схеми Гауса використовуються для СЛАР із розрідженими матрицями довільної структури. В цих схемах застосовується тріангуляція матриць (трикутна декомпозиція) – суть якої полягає в перетворенні матрично-векторного рівняння (1.5) в рівняння з трикутними матрицями (методику перетворення квадратної матриці на добуток двох трикутних наведено нижче).

Порядок дій в методі LU–перетворення наступний:

а) виконується заміна матриці А на добуток двох трикутних матриць L і U; (в матриці U діагональні елементи дорівнюють одиницям);

б) розв'язується відносно Y рівняння ;

в) розв'язується відносно X рівняння .

Методика розкладання матриці на добуток двох трикутних матриць.

Квадратну матрицю можна розкласти на дві трикутні (квадратні, в яких елементи, що розташовані вище (нижче) головної діагоналі, дорівнюють нулю) і це розкладення буде єдиним, якщо діагональним елементам однієї з трикутних матриць заздалегідь дати не рівні нулю значення (наприклад, такі, що дорівнюють одиницям).

Нехай , де Т₁ і Т₂ – трикутні матриці в одній з яких діагональними елементами є одиниці. Інші елементи матриць Т₁ і Т₂ знаходять наступним чином:

а) перемножують матриці Т₁ і Т₂ (їх елементи – літерні позначення);

б) прирівнюють відповідні елементи матриці-добутку Т₁Т₂ елементам матриці А – одержують рівняння: одночленні, двочленні і т. д.;

в) розв'язують одержані рівняння – спочатку одночленні, далі двочленні і т.д.

3.2.2 Ітераційні методи розв'язування СЛАР

Розглядаються три ітераційних метода: метод простої ітерації (послі-

довних наближень), метод Зейделя і метод найшвидшого спуску.

Метод простої ітерації.

В загальному випадку задана СЛАР (3.2), яка записана в розгорнутому матричному вигляді (3.5). Якщо припустити, що діагональні елементи матриці А (і = 1, 2, …, n), то можна перевести систему до канонічного виду і потім виразити х₁ через перше рівняння системи, х₂ – через друге рівняння і т. д. У результаті одержимо систему, яка еквівалентна системі (3.2):

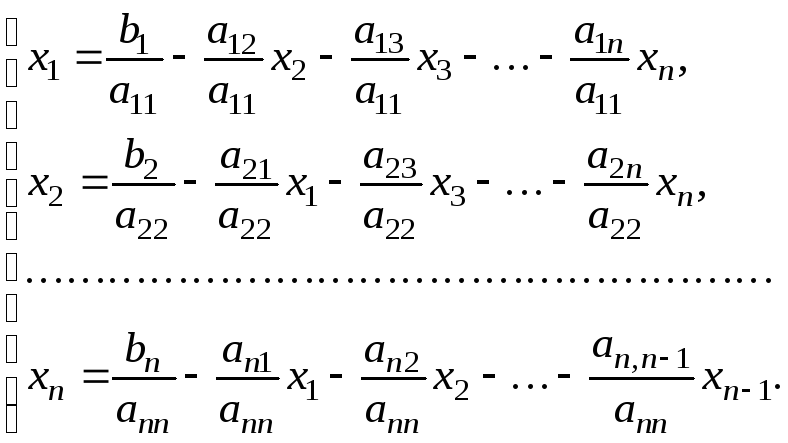(3.9)

Позначимо , де і, j = 1, 2, …, n. Тоді система (3.9) запишеться так:

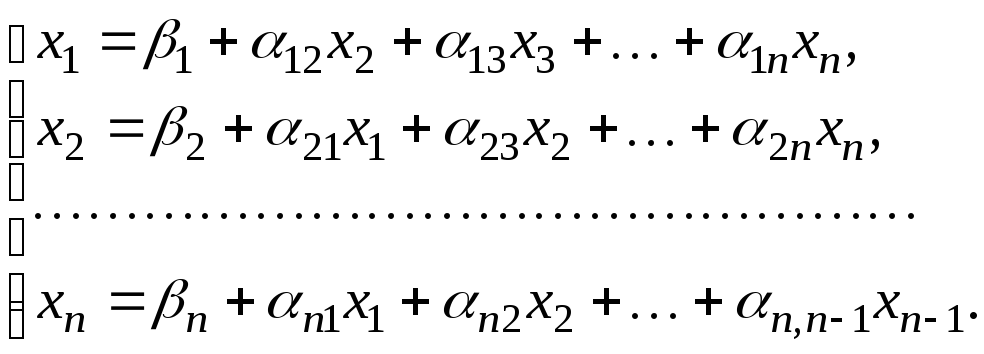(3.10)

Систему (3.10) називають приведеною до нормального виду. Ця система в матричній формі запису:

або

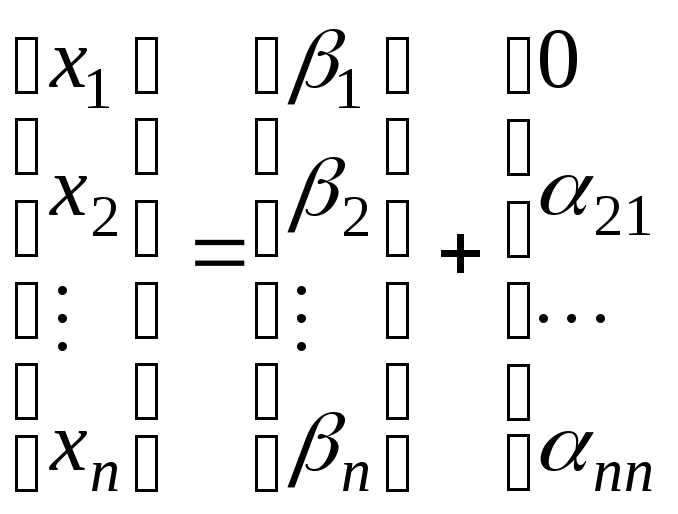
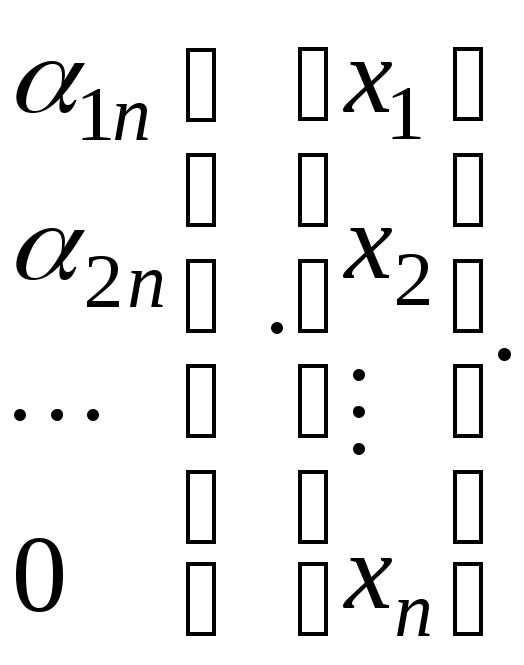(3.11)

Після нормалізації системи перевіряється умова збіжності ітераційного процесу. Ознакою збіжності є умова того, що будь-яка з норм матриці менша від одиниці, тобто

де q – норма матриці , яка може бути визначена за однією із формул:

, .

Алгоритм методу простої ітерації наступний:

- за нульове наближення приймається стовпець вільних членів:

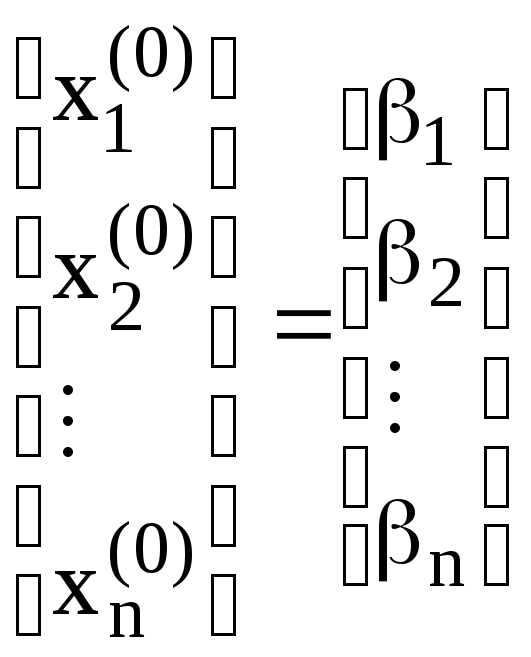– нульове наближення,

далі будуються матриці-стовпці наступних наближень:

– перше наближення;

– друге наближення

і т.д.

Взагалі, будь-яке (k+1)-е наближення обчислюють за формулою

(k = 0, 1, …, n). (3.12)

Ітераційний процес продовжується доти, поки не буде виконано умову

де – задана абсолютна похибка.

В методі ітерацій заміна значень всіх змінних проводиться одночасно (одночасне зміщення).

Приклад 1. Розрахувати струми в гілках електричного кола (рис. 3.1) методом простої ітерації.

У матричному виді система (1.1) запишеться наступним чином (за даними параметрів схеми рис. 1.1):

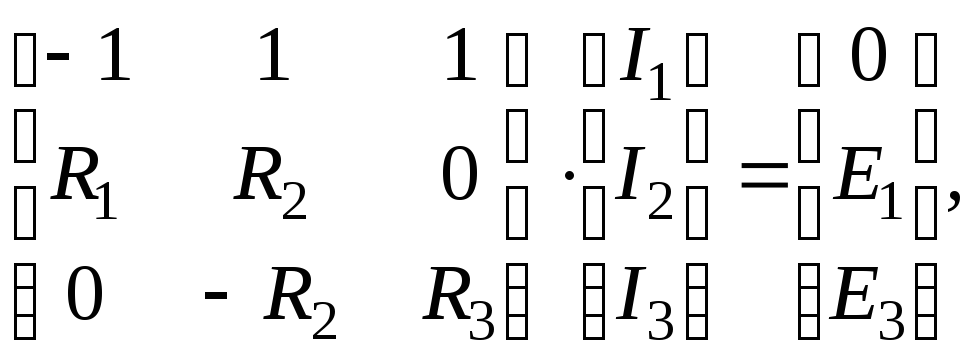або (3.13)

Перед приведенням системи до нормального виду необхідно за допомогою еквівалентних перетворювань зробити систему (3.13) придатну ітераційному процесу. Для цього слід за допомогою перестановки і алгебраїчних дій з рівняннями системи добитися, щоб елементи головної діагоналі матриці мали максимальне за модулем значення. Тобто:

- друге рівняння запишеться замість першого;

- з першого рівняння, домноженого на 10 віднімається третє рівняння і результат записується замість другого рівняння;

- третє рівняння залишається без змін.

В результаті система (1.13) набуває виду:

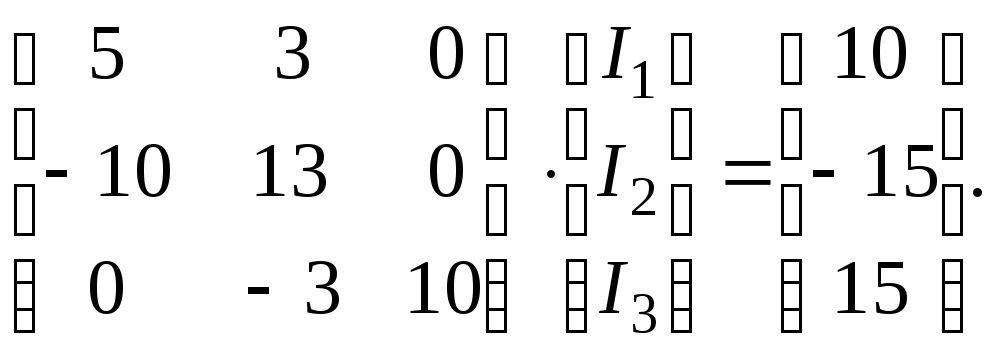(3.14)

Для переводу до нормального виду кожне рівняння системи треба розділити на відповідні елементи, що розташовані на головної діагоналі.

Для СЛАР (3.14), що еквівалентна системі (3.1), нормальний вид наступний:

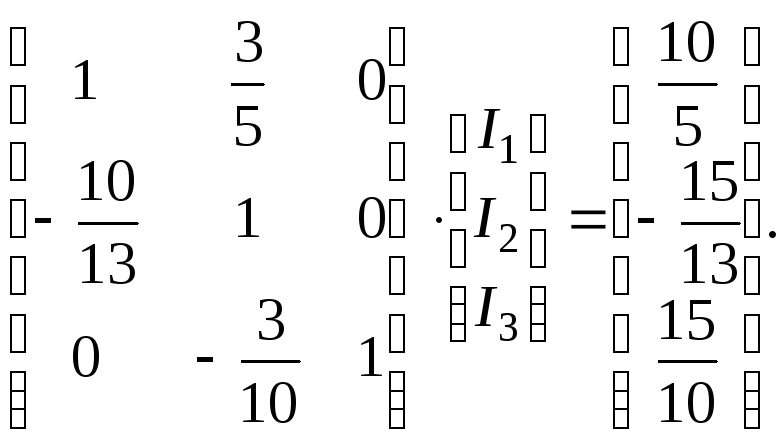(3.15)

Для застосування методу простої ітерації матрична система переписується у формі (3.11), тобто:

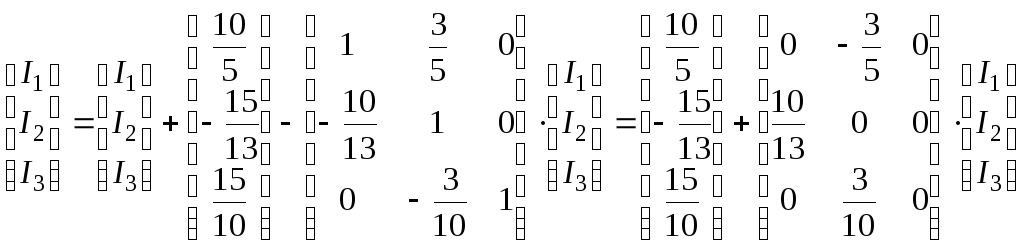.(3.16)

З (3.16) слідує, що і , тобто умова збіжності ітераційного процесу (норма матриці менша від одиниці) виконується як по рядках, так і по стовпцях.

Нульове наближення, що дорівнює з (1.12): .

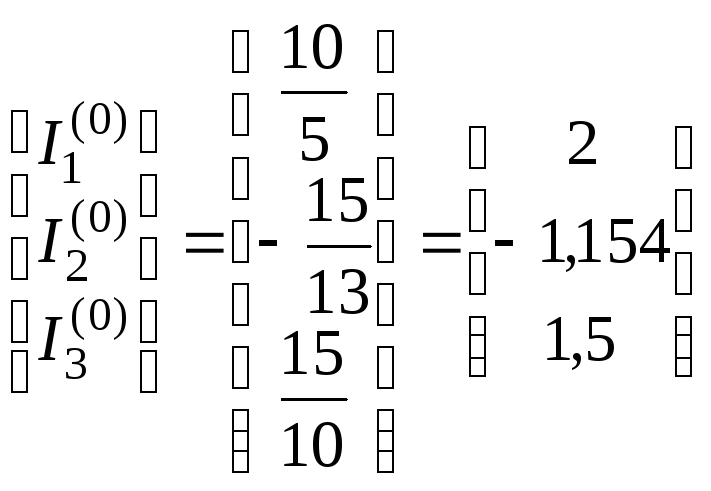Задається абсолютна похибка розрахунку

Перше наближення згідно ітераційній формулі методу (3.12):

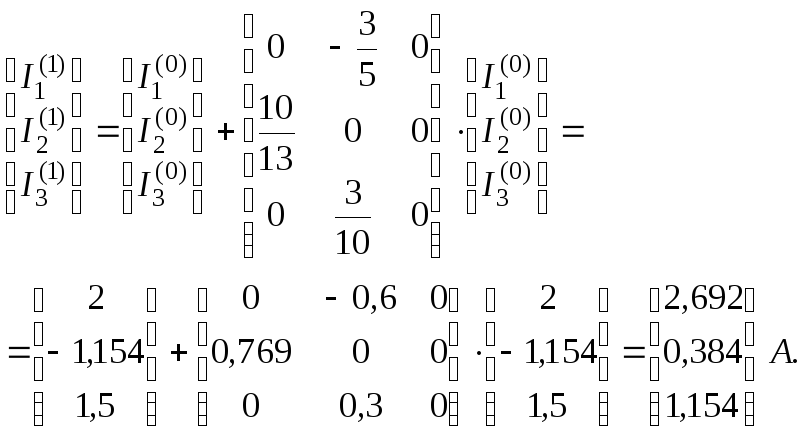
Знаходиться друге наближення:

Третє наближення:

Аналогічно знаходяться наступні наближення розв'язки задачі:

Перевірка умови закінчення ітераційного процесу після 14-го кроку:

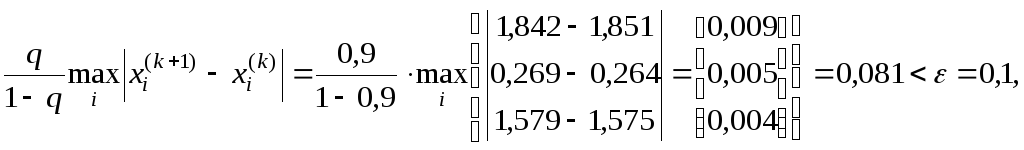
За чотирнадцять кроків ітераційний процес закінчився з заданою точністю.

Струм в гілках схеми (рис. 1.1) становить:

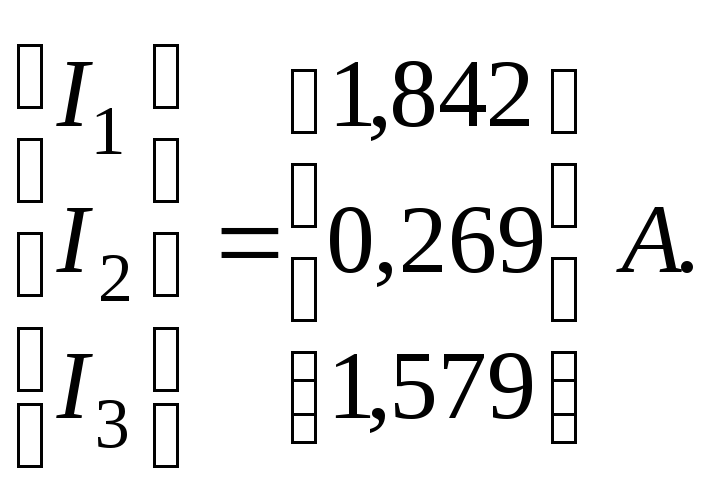
Перевірка у вузлі „а” (рис. 1.1) за першим законом Кірхгофа виконується з точністю до (0,269 + 1,579) – 1,842 = 0,006 А.

Метод Зейделя.

В методі Зейделя уточнене значення х₁ зразу ж використовується для обчислення х₂, далі нові значення х₁ і х₂ використовуються для обчислення х₃ і т. д.

Це невелике удосконалення ітераційної процедури дозволяє суттєво збільшити швидкість збіжності.

Будь-яке (k+1)-е наближення в методі Зейделя будується за наступними формулами:

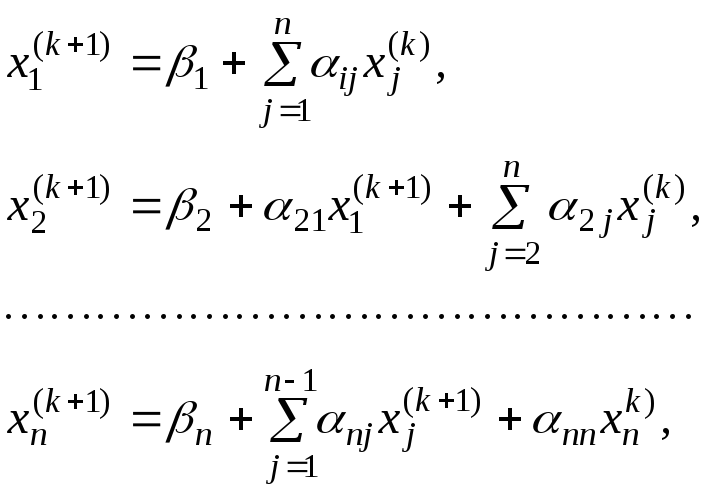(3.17)

де k = 0, 1, 2, …, n.

Ітерації закінчуються, коли із заданою точністю одержано однакові значення невідомих у двох ітераціях підряд.

Умови збіжності ітераційного процесу подібні умовам для простої ітерації, тобто ітераційний процес і його збіжність залежать від величини елементів матриці наступним чином: якщо найбільша сума модулів елементів рядків або найбільша сума модулів елементів стовпців менше одиниці, то процес ітерації для даної системи збігається до єдиного розв'язку незалежно від вибору початкового наближення.

Отже, умови збіжності можна записати так:

(i = 1, 2, …, n) або (j = 1, 2, …, n).

Як і в методі простої ітерації треба привести СЛАР до виду, який придатний для ітерацій. Для виконання умов збіжності ітераційного процесу достатньо, щоб значення елементів матриці при були невеликими з абсолютної величини. Це рівносильно тому, що якщо для СЛАР модулі діагональних коефіцієнтів кожного рівняння системи більше суми модулів всіх інших коефіцієнтів (без врахування вільних членів), то ітераційні процеси для цієї системи збігаються.

Окремо, на прикладі показується, як виконується еквівалентне перетворення вихідної СЛАР і отримується нормалізована система в загальному випадку.

Вихідна СЛАР:

Виконуються наступні дії:

а) в заданій системі виділяються рівняння з коефіцієнтами, модулі яких більші за суму модулів інших коефіцієнтів рівняння. Кожне виділене рівняння записується в таку строку нової СЛАР, щоб найбільший за модулем коефіцієнт був діагональним. В рівнянні (Q) виконується таке: . Рівняння (Q) приймається за третє рівняння нової системи.

б) інші рівняння нової еквівалентної системи одержуються шляхом складання лінійних незалежних між собою комбінацій. Так, за перше рівняння можна прийняти таку лінійну комбінацію (P)+(R), тоді:

.

За друге рівняння нової системи – таку комбінацію: (2Q)+(R)-(P), тобто

.

В результаті одержано перетворену СЛАР яка еквівалентна вихідній і задовольняє умовам збіжності ітераційного процесу:

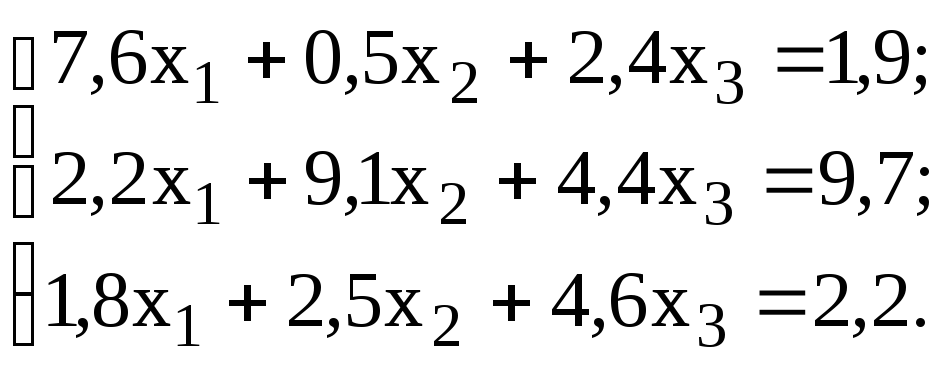
Для перевірки цього твердження еквівалентна система приводиться до нормального виду і перевіряється, чи задовольняється хоч одна з умов збіжності.

При цьому використовується такий спосіб: записуються коефіцієнти при невідомих x₁, x₂, x₃ у відповідних рівняннях системи як m·x, де m – число, що близьке до коефіцієнта при відповідному невідомому і на яке легко розділити коефіцієнти при невідомих і вільні члени.

Наприклад, приймається m = 10. Тоді система, що приводиться до нормального виду, перепишеться так:

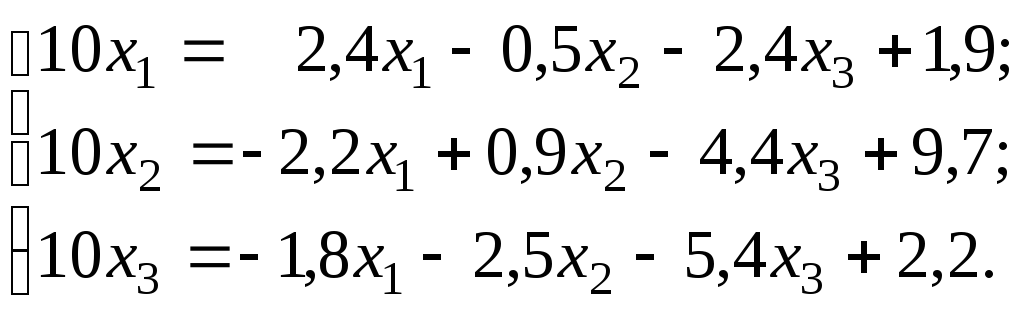
або

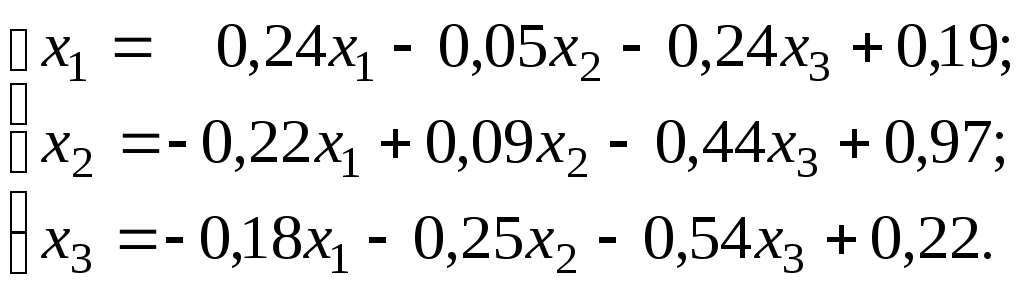
Матриця і вектор приймають вид

, .

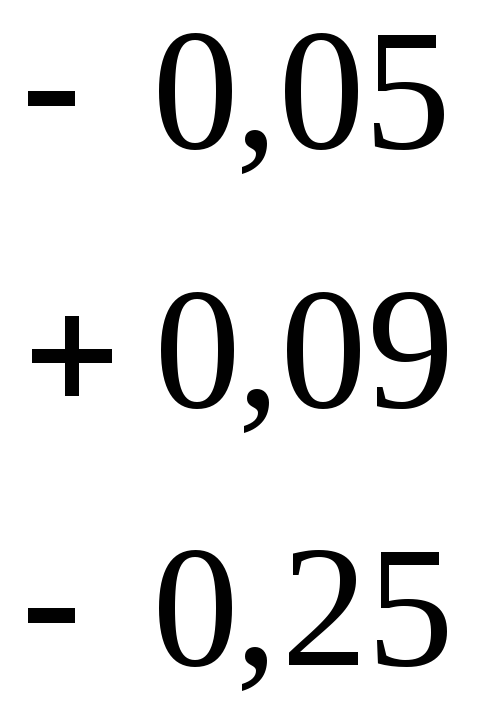
Суми модулів елементів рядків матриці :

0,24 + 0,05 + 0,24 = 0,53;

0,22 + 0,09 + 0,44 = 0,75;

0,18 + 0,25 + 0,54 = 0,97.

Більша із сум 0,97 < 1. Отже, одна з умов збіжності ітераційного процесу виконується. І хоч друга умова не виконується (більша сума модулів елементів стовпців 0,24 + 0,44 + 0,54 = 1,22 > 1) процес ітерації для системи, що розглядається, збігається до єдиного розв‘язку.

Приклад 2. Розрахувати струми в гілках електричного кола (рис. 3.1) методом Зейделя.

Розв'язується СЛАР (3.13) з прикладу 1.

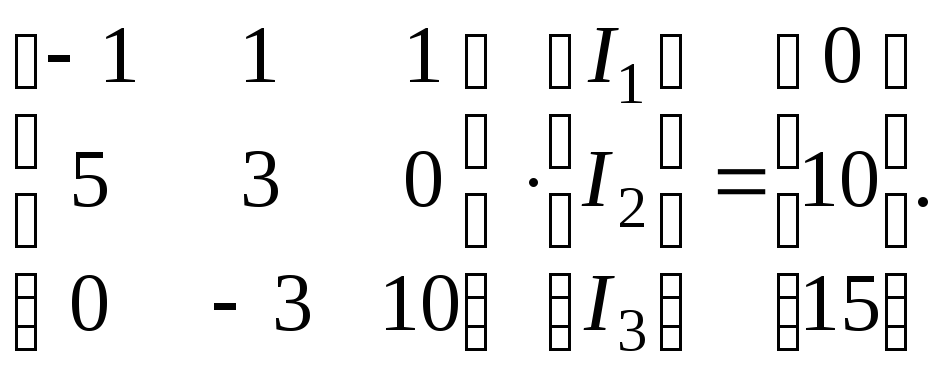
Після еквівалентних перетворювань система має вид (3.14)

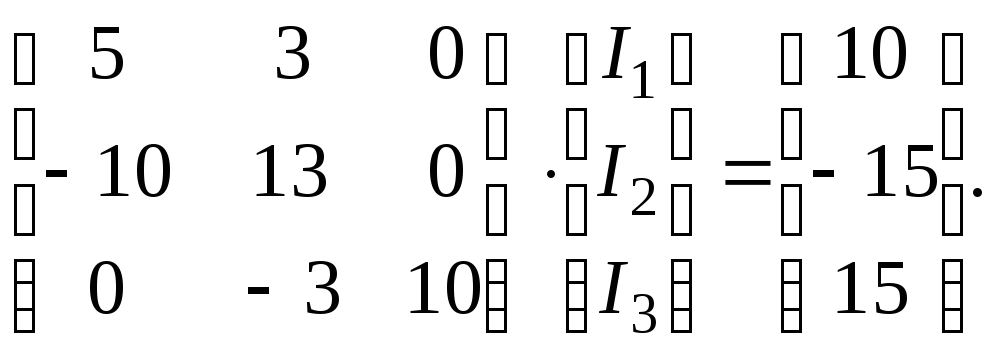
Надалі еквівалентна СЛАР приводиться до нормального виду, що придатний до проведення ітерацій, за допомогою коефіцієнта m = 20, аналогічно попередньому прикладу еквівалентних перетворювань, але з урахуванням матричної форми запису системи рівнянь.

(3.18)

З (3.18) видно, що

,

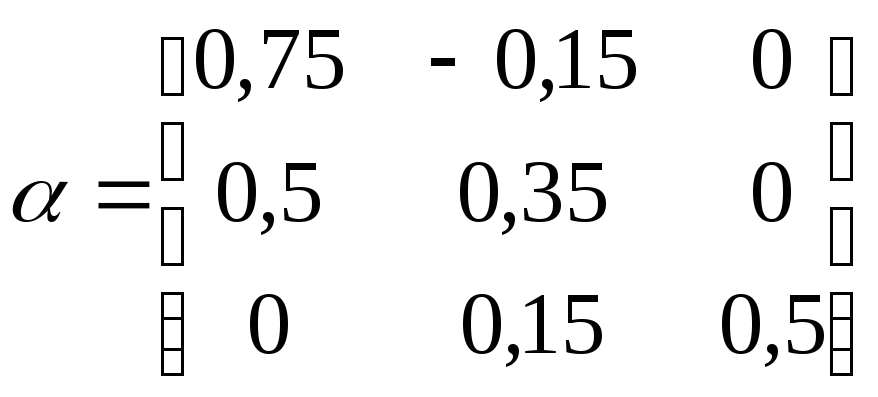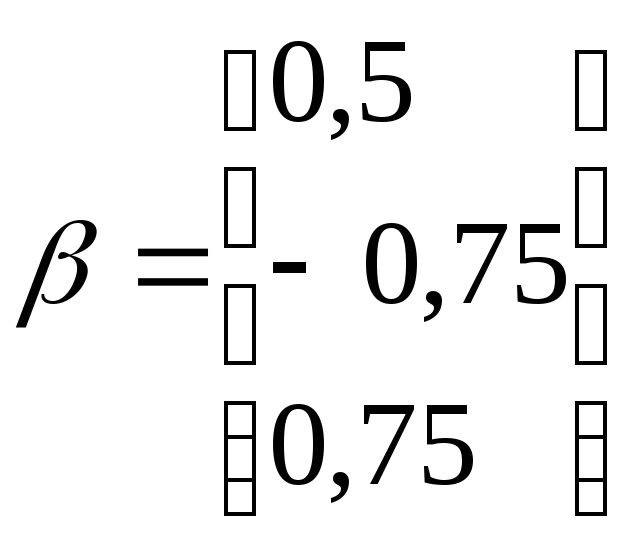
і умова збіжності ітераційного процесу виконується по рядках при .

Нульове наближення, що дорівнює з (3.17):

Задається абсолютна похибка розрахунку

Перше наближення згідно ітераційних формул методу (3.17):

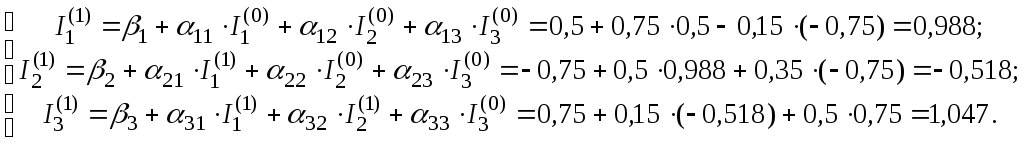
Друге наближення:

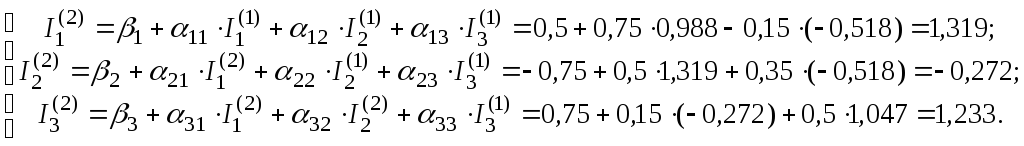
Третє наближення:

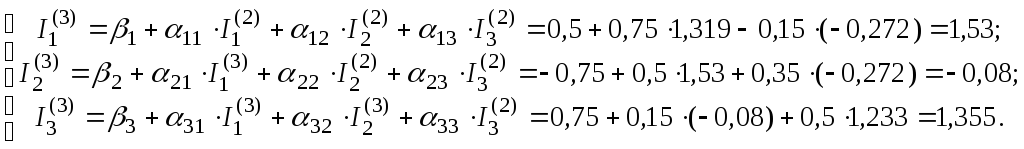
Аналогічно виконуються кроки наступних ітерацій:

Перевірка умови закінчення ітераційного процесу після 9-го кроку:

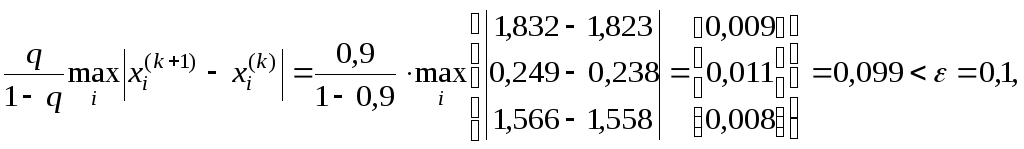
За дев'ять кроків ітераційний процес закінчився з заданою точністю.

Струм в гілках схеми (рис. 1.1) за методом Зейделя становить:

Перевірка у вузлі „а” (рис. 1.1) за першим законом Кірхгофа виконується з точністю до |(0,249 + 1,566) – 1,832| = 0,017 А.