Лекція 5. Наближення функцій

5.1 Способи завдання функцій

З курсу математичного аналізу відомі три способи завдання функціональних залежностей: аналітичний, графічний, табличний.

Найбільш зручним способом завдання функціональної залежності є аналітичний, тому що він прямо вказує дії і послідовність їх виконання над незалежною змінною х для одержання відповідного значення величини y. Позитивна властивість способу полягає в можливості одержувати значення y для будь-якого фіксованого аргументу х із будь-якою точністю.

Графіком функції є геометричне місце точок площини х0у, координати яких задовольняють рівнянню .

Табличний спосіб завдання функцій частіше всього виникає в результаті експерименту і має перевагу в тому, що для кожного значення незалежної змінної, що уміщене в таблицю, можна без усяких вимірів і обчислень знайти відповідне значення функції. Недолік табличного способу полягає в тому, що не можна задати всю функцію безперервно – завжди будуть такі значення незалежної змінної, котрих нема в таблиці. Крім того виникають труднощі дослідження характерних особливостей заданої функції (визначення похідних і т. і.).

5.2 Формулювання задачі наближення функцій

Важним і цікавим є питання переходу від табличного способу завдання функції до аналітичного. Це дозволить уникнути вказаних вище недоліків табличного способу завдання функції.

Можна сформулювати таку задачу: нехай за допомогою таблиці (табл. 5.1) задано функцію . Знайти по можливості простий аналітичний вираз цієї функції.

Таблиця 5.1 – Функція

x				…
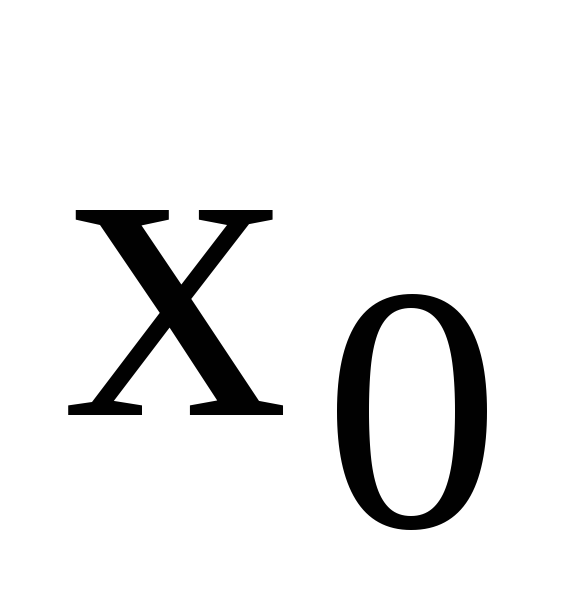
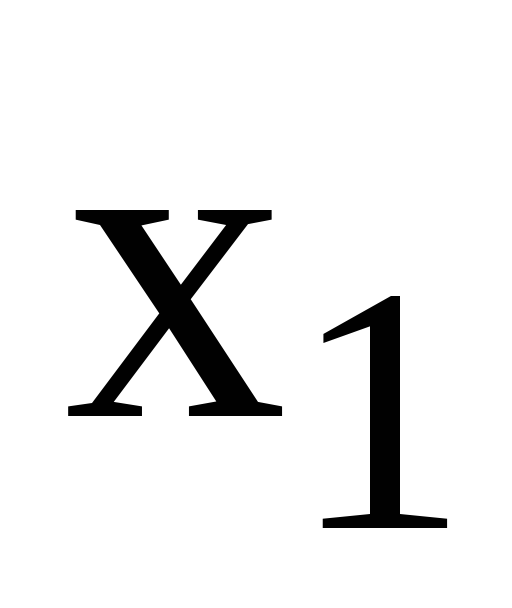
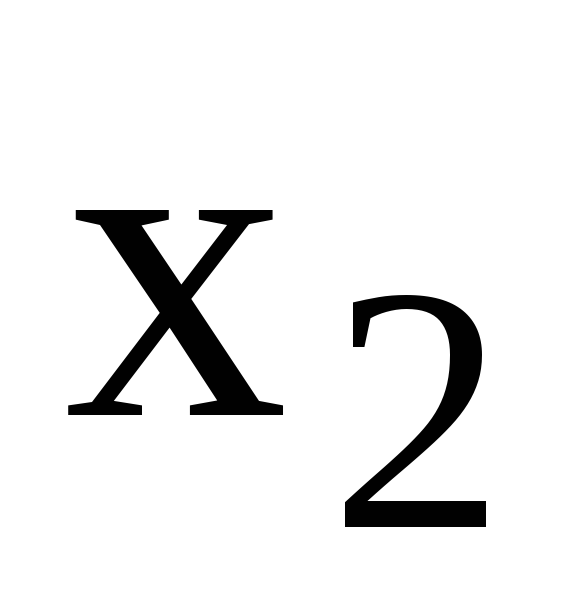
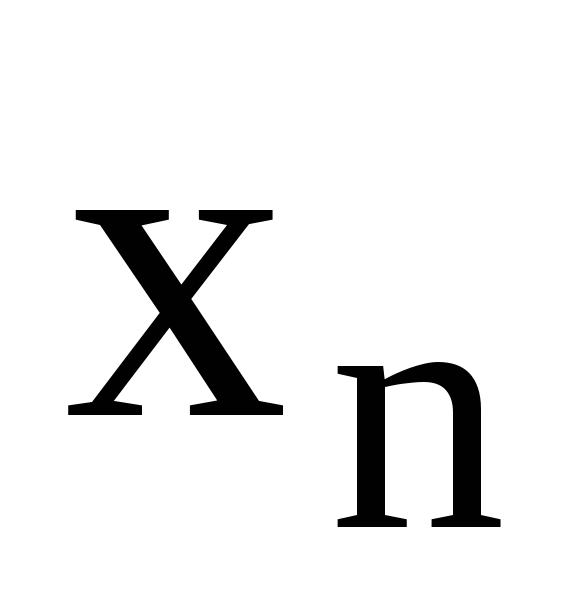
y				…

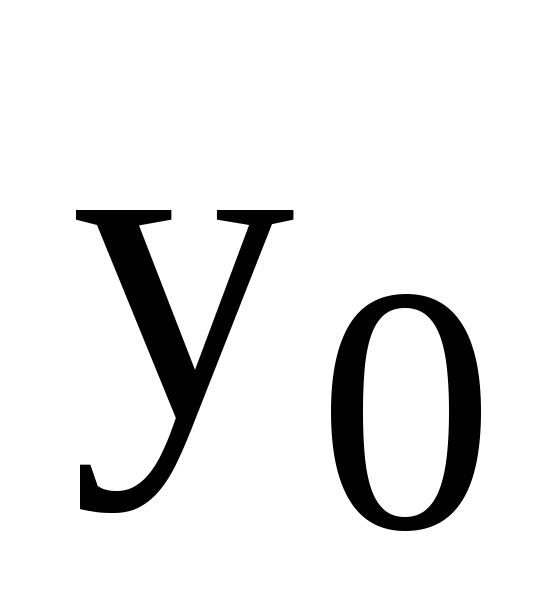
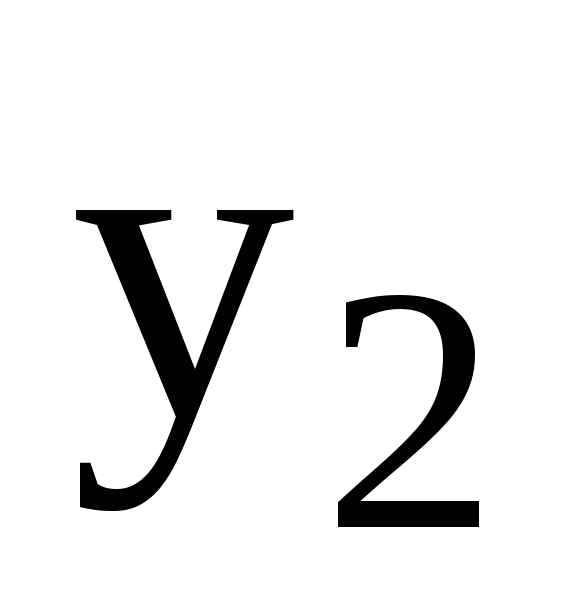
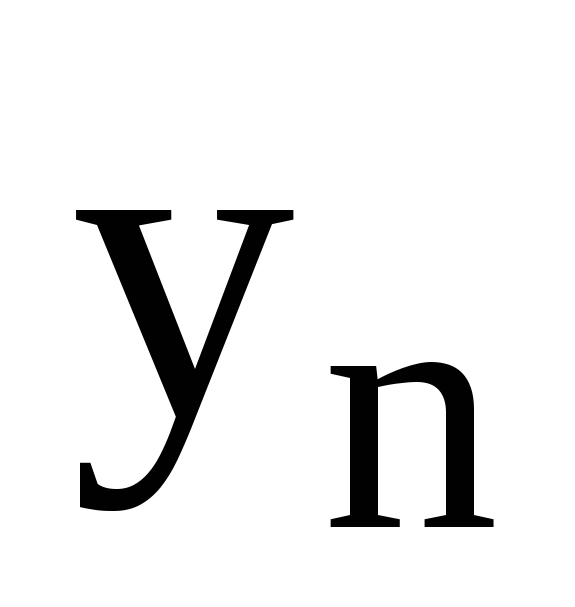
Спочатку задаються видом функції. Для цієї мети практично важливим є використання поліномів:

– алгебричного

; (5.1)

– тригонометричного

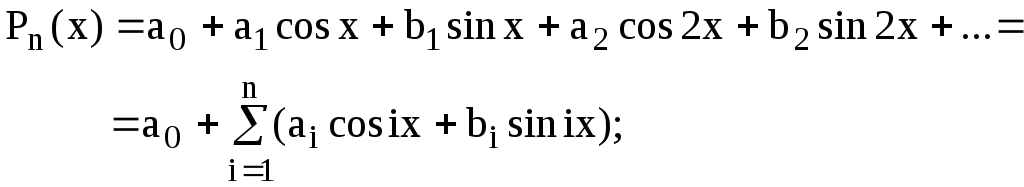(5.2)

– експоненціального

(5.3)

Після того, як вид функції задано, стає задача визначення невідомих коефіцієнтів а_і (b_i) так, щоб досягти найменшого відхилення поліному від заданої функції у(х). Що стосується терміну «найменше відхилення», то може бути два випадки.

В першому ставиться задача точного відтворення всіх значень функції, що задані в табл. 5.1. Така задача називається інтерполяцією функції.

В другому випадку, коли табличні дані одержані, наприклад, в експерименті і містять експериментальні похибки, коефіцієнти полінома знаходять так, щоб вказані в табл. 5.1 значення функції описувались наближено (нема сенсу повторювати помилки, які були допущені в експерименті). Така задача називається апроксимацією функції.

5.3 Інтерполяція функцій

Загальна задача інтерполяції полягає в наступному: для заданої в вигляді таблиці функції побудувати багаточлен, що приймає в заданих точках х_і ті ж значення, що й функція у(х), тобто

(5.4)

Точки називаються вузлами інтерполяції. З геометричної точки зору це означає, що графік інтерполяційного многочлена має проходити через задану сукупність точок Але в такій загальній постановці задача інтерполяції до кінця не визначена, тому що через задану систему точок можна провести нескінченну кількість кривих. Задача стає однозначною, якщо задатися конкретним видом поліному ступеня не вище n.

Розглянемо, наприклад, інтерполяцію з використанням поліному (5.1). Нехай з табл. 5.1 відомі значення Тоді з умови (5.4) одержимо систему рівнянь відносно невідомих a₀, a₁, a₂, …, a_n

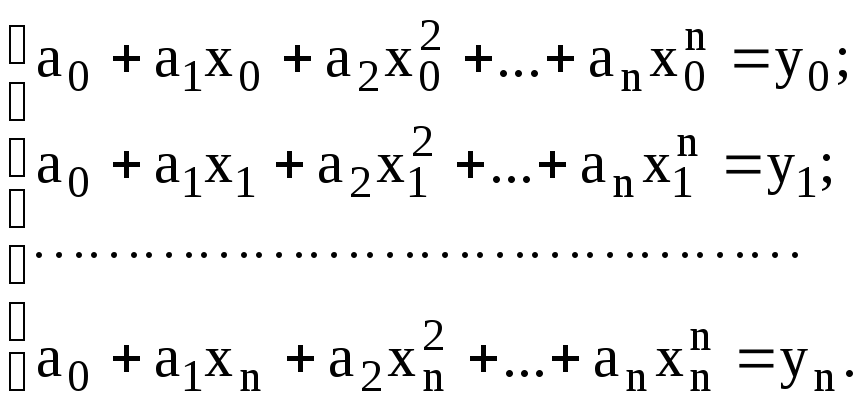(5.5)

Можна довести, що якщо серед вузлів інтерполяції нема таких, що збігаються ( при , то головний визначник системи (5.5)

,

який називають визначником Вандермонда, не дорівнює нулю. Згідно з правилом Крамера це означає, що система (5.5) має єдиний розв‘язок.

Поліном , коефіцієнти котрого визначаються із системи (5.5), називається інтерполяційним поліномом Лагранжа і позначається

Однак, безпосереднє розв‘язання системи (5.5) – задача вельми трудомістка при великій кількості вузлів. Тому будемо шукати поліном у вигляді лінійної комбінації поліномів ступеня n:

(5.6)

При цьому необхідно, щоб кожний поліном перетворювався в нуль у всіх вузлах інтерполяції за винятком одного (і-го), де він має дорівнювати одиниці. Таким умовам відповідає поліном виду

. (5.7)

Підстановка (5.6) в (5.7) дає

, (5.8)

або в більш компактній формі запису

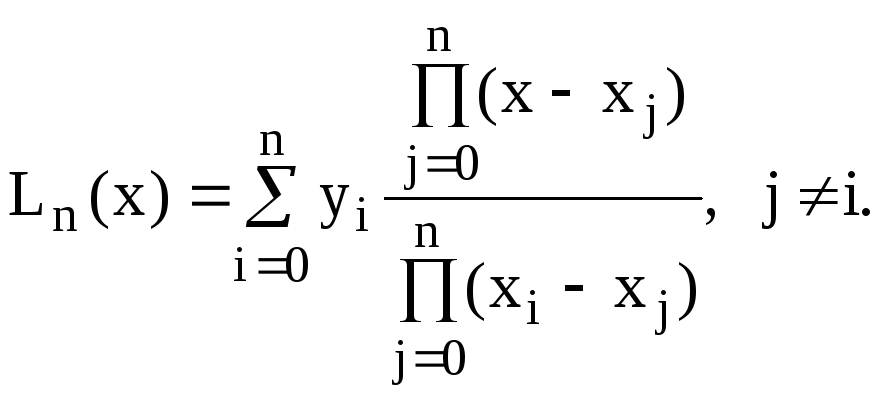
На практиці часто зустрічаються задачі, де відстань між сусідніми вузлами інтерполяції однакова, тобто Для випадку рівновіддалених вузлів формула Лагранжа (5.8) може бути записана в іншому вигляді, а саме у вигляді так званої першої інтерполяційної формули Ньютона

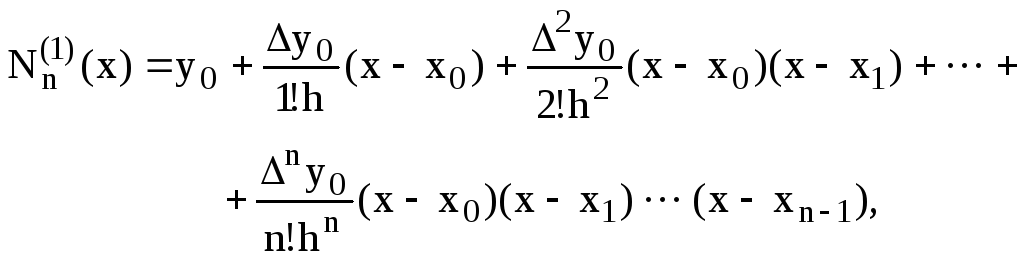
(5.9)

де – кінцеві різниці першого, другого, …, n-го порядку відповідно. Вони обчислюються так:

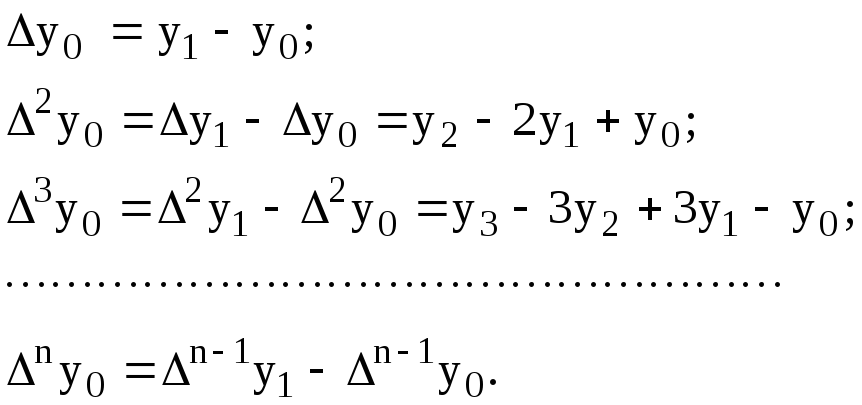
Визначення кінцевих різниць зручно робити у вигляді діагональних таблиць (наприклад, табл. 5.2).

Часто використовують першу формулу Ньютона в іншому виді. Введемо нову змінну

де h – крок, а q – кількість кроків.

Таблиця 5.2 – Діагональна таблиця кінцевих різниць

x	y

Тоді перша інтерполяційна формула Ньютона прийме вид

(5.9')

Формули (5.9) і (5.9') зручно використовувати для інтерполяції на початку таблиці, де q – мале число.

Для інтерполяції в кінці таблиці використовують другу інтерполяційну формулу Ньютона, яка також має дві форми запису:

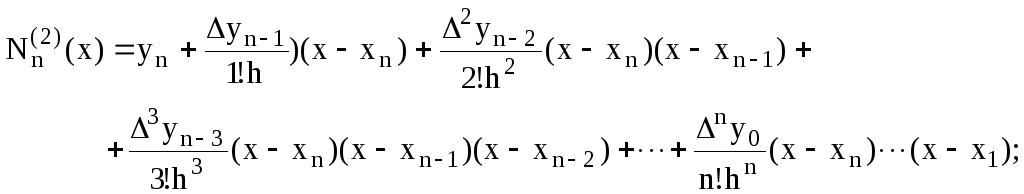
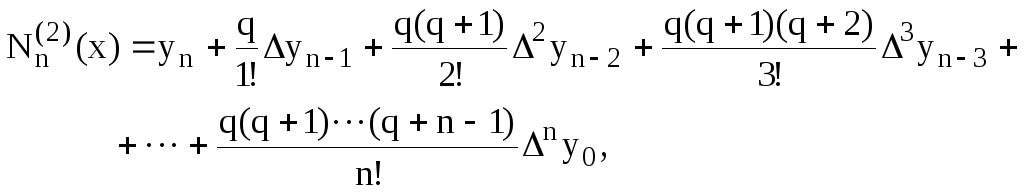
(5.10)

(5.10')

де

Для інтерполяції в середині таблиці використовують інтерполяційні формули Гаусса. В цих формулах застосовуються так звані таблиці центральних різниць, відмінність яких від діагональних таблиць видно із порівняння таблиць 5.2 і 5.3.

Перша інтерполяційна формула Гауса

(5.11)

Таблиця 5.3 – Таблиця центральних різниць

x	y	Δy	Δ2y	Δ3y	Δ4y	Δ5y	Δ6y
···	···	···	···	···	···	···	···
···	···	···	···	···	···	···	···

В першій інтерполяційній формулі Гаусса використовуються центральні різниці

що розташовані в рядку і в наступному за ним рядку.

В другій інтерполяційній формулі Гаусса використовуються центральні різниці із рядка і із рядка, розташованого над ним

,

Друга інтерполяційна формула Гауса має вид

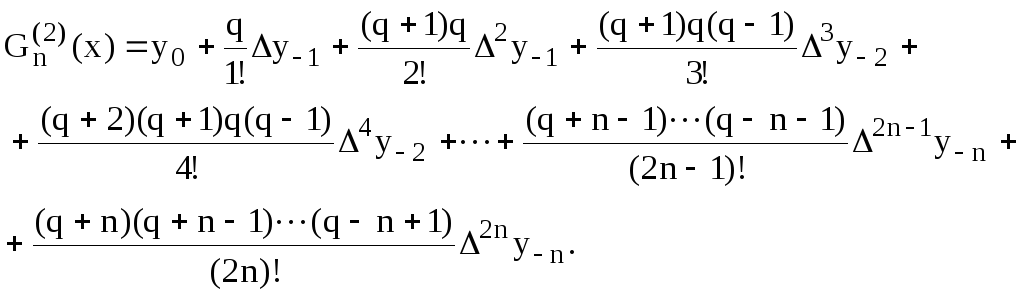
(5.12)

Для обох формул Гаусса

Слід відмітити, що при заданому табличному наборі вузлів інтерполяції існує тільки один інтерполяційний поліном. Тому формули Лагранжа, Ньютона, Гаусса і ін. дають один і той же поліном. Різниця тільки в формі їх запису.

Опис поведінки функції на всьому інтервалі зміни аргументу за допомогою одного інтерполяційного многочлена називається глобальною інтерполяцією. Велика кількість табличних даних потребує в цьому випадку і високого ступеня многочлену. Часто це буває незручно і навіть приводить до погіршення точності (це виявив у 1901 р. Рунге).

Більшу перевагу іноді має локальна інтерполяція, при якій інтерполяційні многочлени будуються окремо для різних частин діапазону зміни аргументу х. Для найпростіших випадків локальної інтерполяції часто буває достатнім використання формул (5.9), (5.9') при кількості вузлів інтерполяції n = 1 (лінійна інтерполяція) і n = 2 (квадратична інтерполяція).

Таким чином, при лінійній інтерполяції значення функції (яка задана таблицею) в інтервалі наближаються формулами:

; (5.13)

. (5.13')

При квадратичній інтерполяції в інтервалі формули наближення набувають такий вигляд:

; (5.14)

(5.14')

Як правило, інтерполяційні багаточлени використовуються для наближення функції в проміжних точках між крайніми вузлами інтерполяції, тобто при Однак іноді вони використовуються і для наближеного обчислення функції поза відрізка, що заданий таблицею (). Таке наближення називають екстраполяцією.