Пути построения оптимальных систем.

1. В этом случае САУ оптимизируют на основе подбора и использования существующих методов анализа систем. В данном случае рассматриваются различные варианты систем с различными параметрами и законами регулирования. Затем расчеты сравниваются, и выбирается вариант, для которого принятый критерий имеет максимальное или минимальное значение.

2. Заключается в непосредственном определении оптимальной системы. Здесь существует 2 способа:

- задается структура системы и требуется найти оптимальное значение ее параметров, которые обеспечивают экстремумы выбранного критерия.

- система считается полностью неизвестной и требуется определить ее характеристики, обеспечивающие достижение экстремума критерия, идеального из всех числовых значений параметров.

Чаще всего значение критерия оптимизации определяется не текущим состоянием объекта, а его поведение в течение всего процесса управления. Поэтому критерий оптимальности можно представить в виде:

,

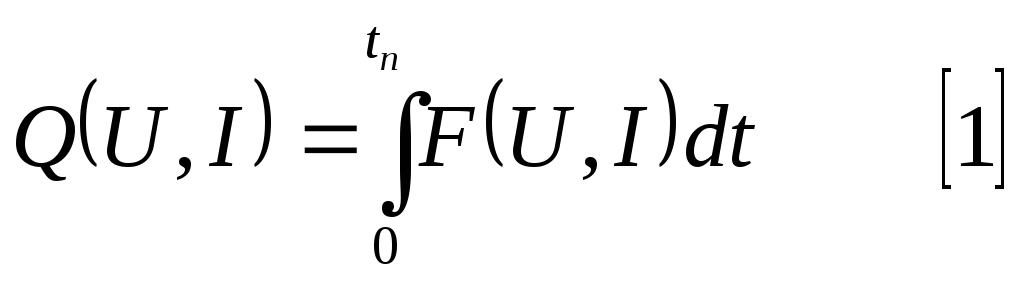где:

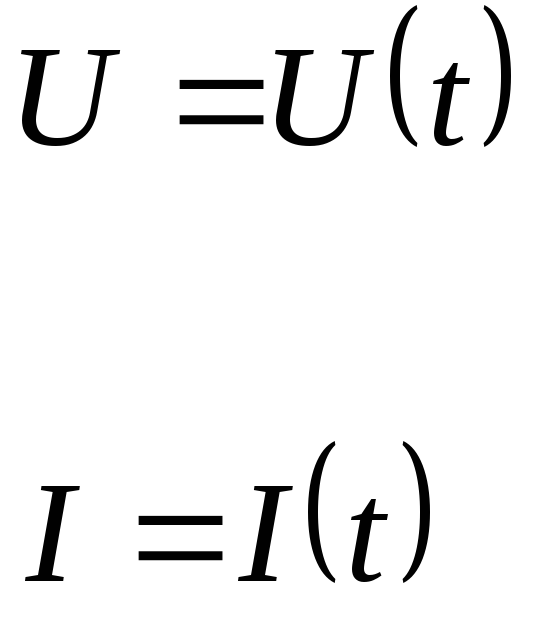
В общем случае - есть вектора:

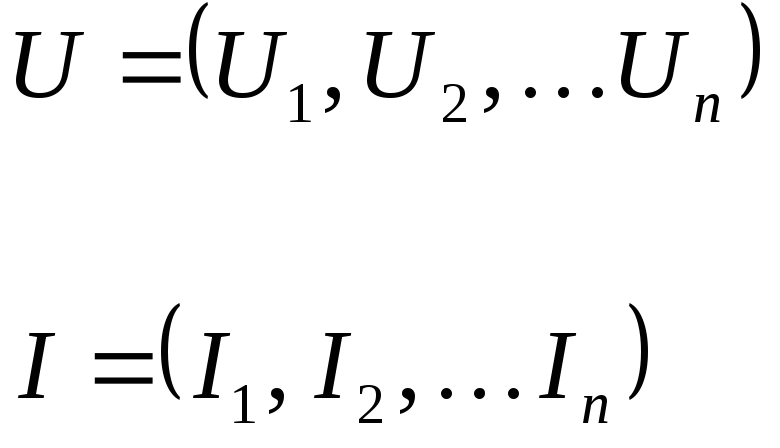
- время переходного процесса системы.

При решении задач оптимизации на величину выходного параметра и управляющего воздействиямогут накладываться некоторые ограничения, которые можно записать в виде следующего неравенства:

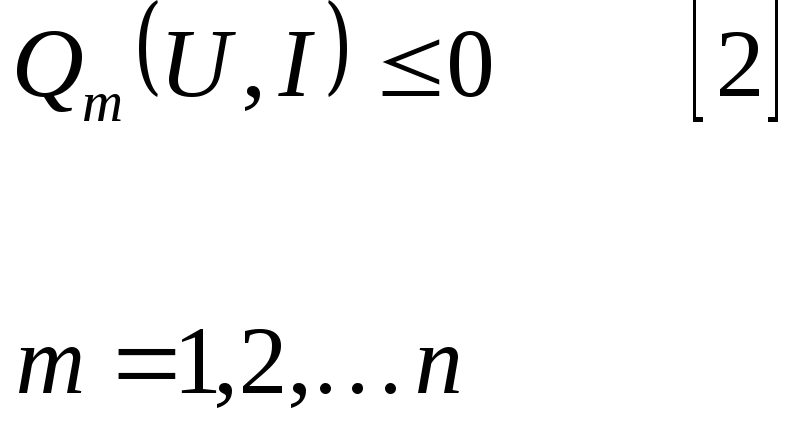
В предельном случае эти ограничения могут быть сведены к ограничениям, накладываемым на отдельные выходные величины. При решении задач оптимизации объект управления можно описать с помощью некоторого оператора :

- выходная величина объекта.

Чаще всего описание объекта задается с помощью системы дифференциальных уравнений.

Для решения уравнений необходимо задать граничные условия при t=0 и конечное состояние объекта управления G. В этом случае задача синтеза будет иметь следующий вид.

По заданному систематическому описанию объекта (в виде дифференциальных уравнений), граничными условиями (при t=0), ограничением вида [2]; внешнего воздействия Х и критерия оптимизации [1], а также устройству управления, обеспечивающего такое оптимальное управление при котором достигается цель управления при максимальном либо минимальном значении параметра оптимизации и выполнении всех ограничений.

Методы решения задач оптимизации. Принцип максимума Понтрягина.

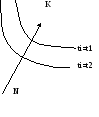
Перевести за минимальное время изображающую точку из некоторого начального положения N в определенную конечную точку К.

Каждой точке фазового пространства окружающего точку К, соответствует оптимальная траектория и соответствующее ей минимальное время перехода в эту точку. Вокруг точки К можно построить поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем ti перехода в эту точку.

Эти поверхности называются изохронами. Оптимальная по быстродействию траектория из точки N в точку К должна быть максимально близка к нормалям насколько это позволяют ограничения, наложенные на величины управления. Движения вдоль изохрон увеличивает время процесса, так как приводит к дополнительным затратам времени на движение не уменьшающее расстояние до конечной точки, то есть на всей траектории произведение вектора скорости изменения выходной величины на вектор, обратный градиенту времени перехода в конечную точкудолжен быть максимальным, то есть должно выполняться условие равенства:

Для любого критерия оптимальности поверхности постоянного значения будут называться изоповерхностями и будет выполняться условие [1]. При практическом определении оптимального управления и оптимальной траектории изоповерхности не определяют, а находят вектора с помощью сопряженных уравнений:

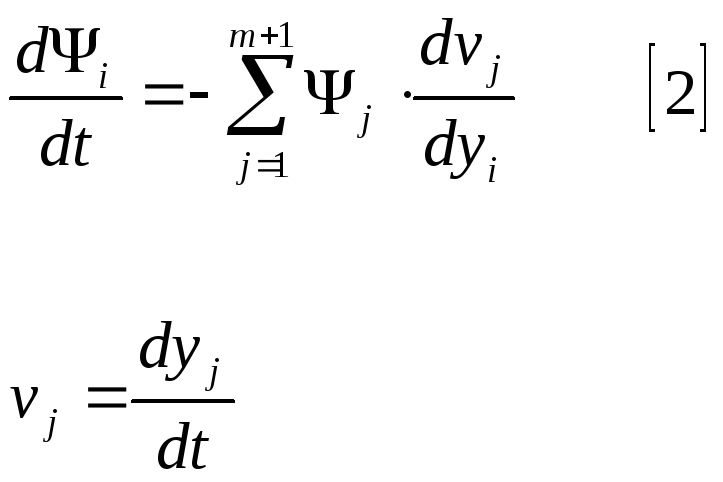
Обозначим сумму произведений:

Определим производную:

Подставим полученное значение в [2].

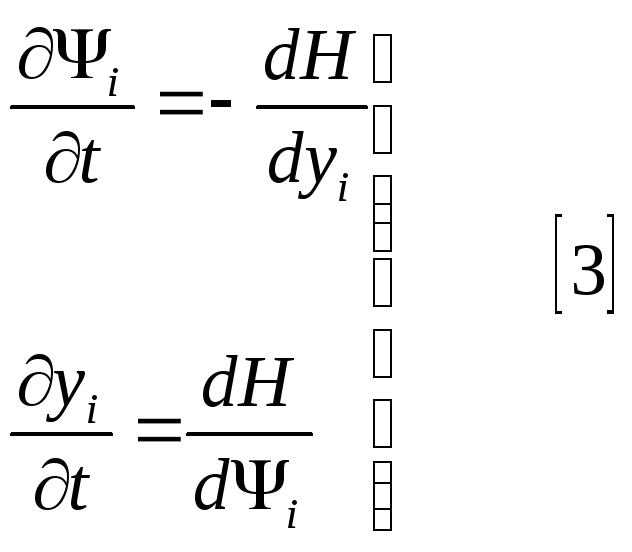
Полученное выражение называется уравнениями Гамильтона, а Н - гамильтонианом. В итоге задача сводится к следующему: определить закон управления , дающее в результате совместного решения уравнения объекта и сопряженных уравнений такую траекториюI(t), для которой гамильтониан Н во всех ее максимумах будет иметь максимальное значение, то есть будет выполняться равенство:

Однако в этом случае необходимо начальное условие и задавая для него произвольные значения, находим траекторию, которая близка к оптимальной, и последовательно приближая ее, получаем оптимальную траекторию.