Поведение функции в окрестностях бесконечно удаленной точки.

Рассмотрим поведение регулярной функции в окрестностяхбесконечно удаленной точки. Примем. Сама точкапереходит в.называется регулярной в бесконечности, если преобразованная функциярегулярна в точке.

Регулярная функция в точкеразлагается в ряд Тейлора и имеет следующий вид:

Возвращаясь в разложении [1] к получаем разложение в точкеравной бесконечности:

Бесконечно удаленная точка , может быть изолированной точкой однозначного характера, тогда разложение функции в окрестности точкиимеет вид:

В этом случае главной частью разложения [3] является , а правильной частью -.

Определим коэффициенты ряда [3]. Для этого рассмотрим окружность , удовлетворяющую условию.. Окружность обходит в положительном направлении по отношению к часовой стрелки. Заменив в [3]наи умножая наи проинтегрировав по Г, получаем:

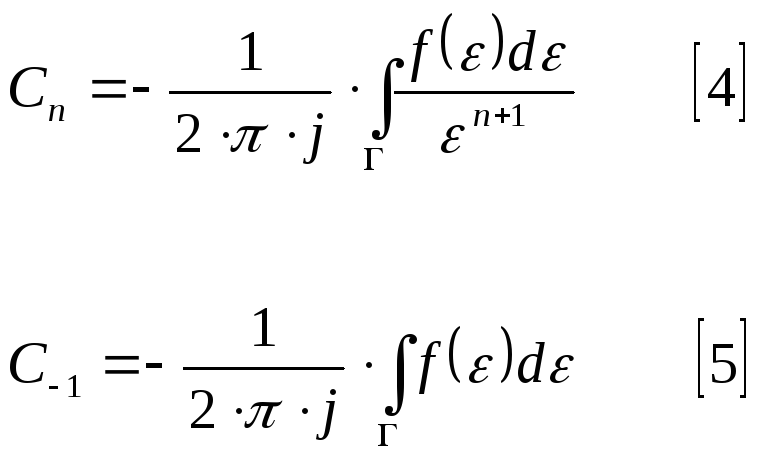
Вычетом функции в точкеявляется взятый со знаком « - » коэффициентприв разложении [3].

Теорема.

Пусть - регулярная функция, имеющая в расширенной плоскости комплексных переменных только изолированные особые точки, тогда сумма вычетовво всех особых точках равна 0.

Доказательство.

Пусть Г – окружность в которой находится изолированная особая точка z с радиусом :. Радиус настолько большой, что все особые точкинаходятся внутри этой окружности. Согласно теореме о вычетах:

Г – обходит точки против часовой стрелки, тогда [7] примет вид:

Подставим [7] в [8], тогда:

Пример:

Вычислить .

Функция имеет 4 простых полюса:

Точка является правильным нулем функции. Разложение функцииимеет вид:

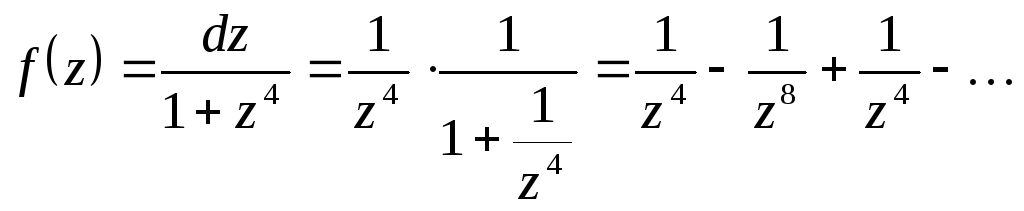
, то .

Применение вычетов.

Пример:

Функция . Найти вычет функции в замкнутом контуре

Г – окружность.

Найдем полюсы:

- простой полюс.

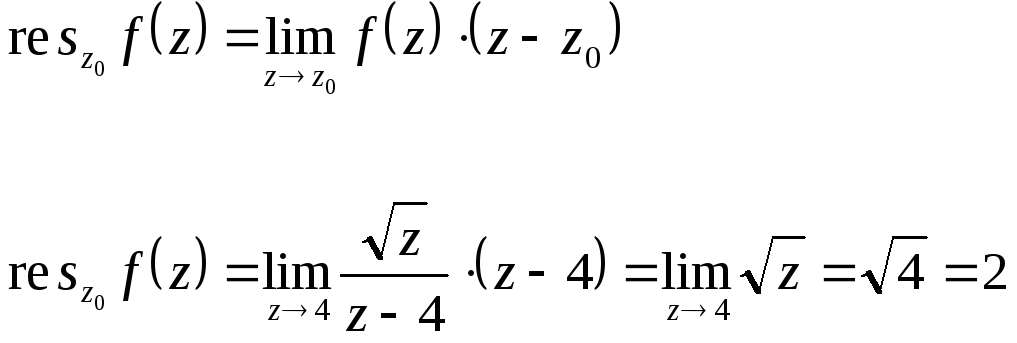
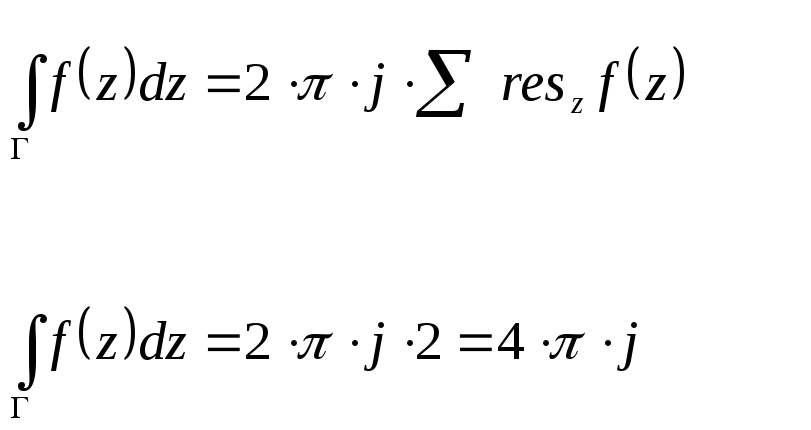
Пример 2.

2 простых полюса:

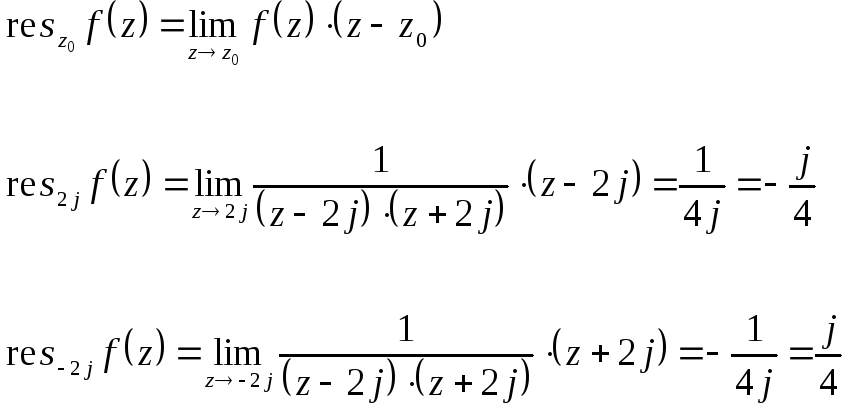
Интегралы вида:

,

где R – рациональная функция от синуса и косинуса, сводится к решению интеграла по окружности , гдеz заменяют на , тогда по формуле Эйлера:

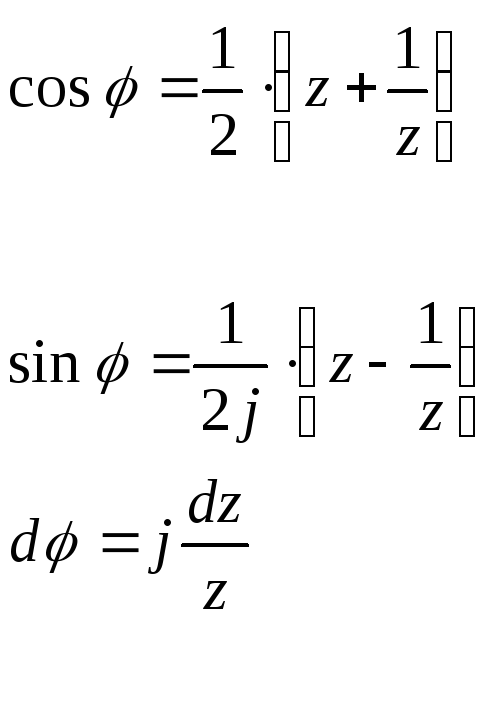
Вопросы для самоконтроля.

1. Что называется изолированной особой точкой.

2. Что такое вычет функции.

3. Сформулируйте теорему о вычетах.

4. Как может вести себя функция в окрестностях изолированной особой точки.

5. Как может быть применима теория о вычетах.

Лекция 6. Оптимальное управление.

Цель. Изучить построение оптимальных систем управления.

Задачи:

1. Изучить теорию построения оптимальных систем.

2. Изучить методы построения оптимальных систем.

САУ, обеспечивающие наилучшее или оптимальное значение какого-либо показателя качества системы, называются оптимальными САУ. Величина, характеризующая качество системы, ее минимальное или максимальное значение называют критерием оптимальности. На параметры системы могут накладываться какие-либо ограничения. Их также необходимо учитывать при определении наилучшего значения параметра оптимизации. В случае, если при синтезе САУ необходимо определить несколько наилучших значений параметров оптимизации в этом случае поступают одним из 2 способов:

1. Из всех параметров оптимизации составляют один интегральный параметр и для него решают оптимизационную задачу.

2. Для каждого параметра оптимизации ищут варианты решения. При этом остальные параметры используют в качестве ограничений. Из всех полученных решений выбирают одно наиболее удовлетворяющее поставленным требованиям.