Свойства рядов Лорана.

1. Ряд Лорана представляет собой сумму 2 функциональных рядов:

- главная часть

- правильная часть

2. Ряд Лорана абсолютно сходится всюду в кольце сходимости:

Главная и правильная части являются рядами по степеням:

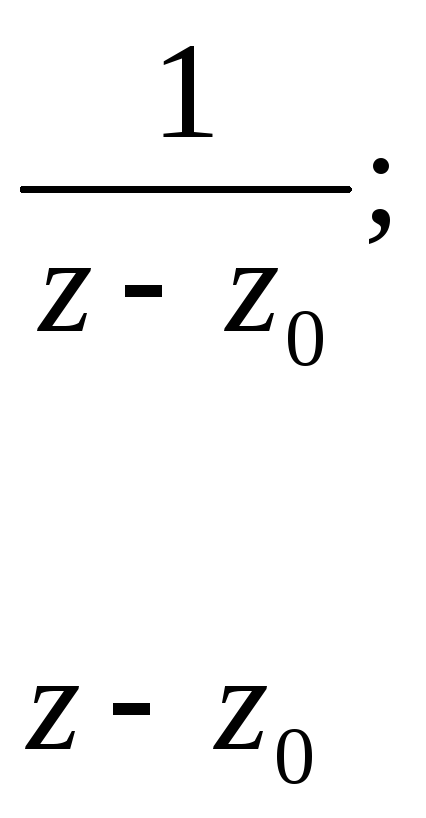
3. Ряд Лорана сходится абсолютно и равномерно в любом замкнутом кольце, расположенным внутри кольца сходимости, то есть для всех z, удовлетворяющих условию:

4. Ряд Лорана можно интегрировать почленно по любому контуру целиком, лежащим внутри кольца сходимости и дифференцировать его внутри кольца сколь угодно раз.

Классификация изолированных особых точек.

Пусть регулярная аналитическая функция в некоторой окрестности точки, то есть при, а в самой точкефункциялибо не аналитична, либо не определена, тогдаявляется особой изолированной точкой.

Функцию в окрестности точки, можно разложить в ряд Лорана:

Ряд [1] используется для классификации особых точек однозначного характера. Если все коэффициенты главной части ряда при всехk<0 равны 0, то является устранимой особой точкой и тогда:

Если в главной части ряда [1] имеется лишь конечное число отличных от 0 коэффициентов, то и в этом случае является полюсом, а

Степень разложения разности «n» является порядком полюса.

Исследуем связь между полюсом функции и нулем функции.

Точка называется правильным полюсом функции. Еслирегулярна в точке, а.

Ряд Тейлора в окрестности нуля имеет вид:

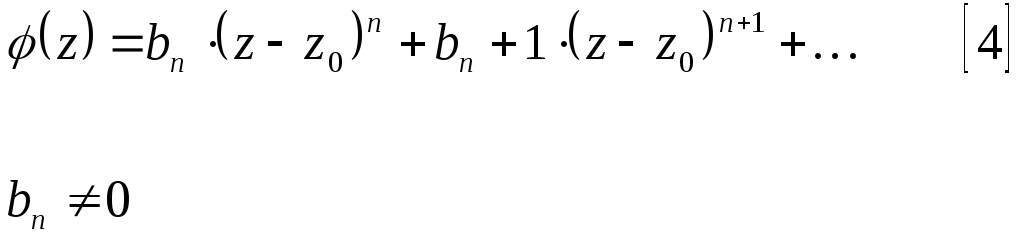
При n=1, полюс называется простым.

Теорема.

Для того, чтобы точка была полюсом порядкаn для функции необходимо и достаточно, чтобы она была нулем кратностиn для функции .

Доказательство.

Пусть является полюсом порядкаn для при:

Функцию представим в виде :

,

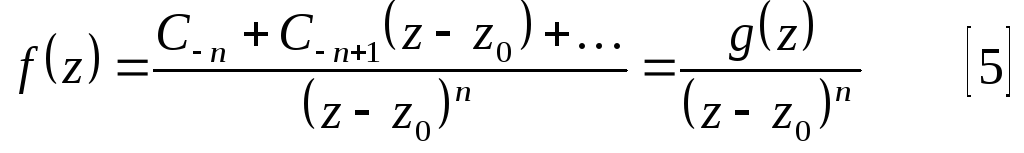где - регулярная функция в точке, причем:

.

Функция также регулярна в точкеи коэффициенты ее разложения находим, используя правило дифференцирования. В итоге получим:

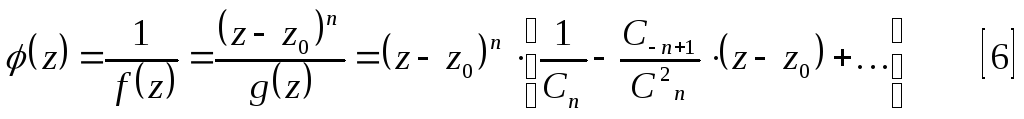
Из этого выражения видно, что является нулем кратностиn для функции .

Согласно [4] получим:

,

где регулярна в точке:

Функция также регулярна в точке.

Найдем коэффициенты разложения этой функции, используя правило дифференцирования:

.

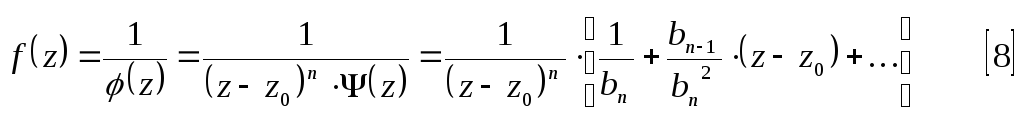Из [8] видно, что является полюсом порядкаn для функции .

Вопросы для самоконтроля.

1. Для чего используется разложение функции в ряд Лорана.

2. Свойства ряда Лорана.

3. Что такое полюс функции.

4. Что такое простой полюс функции.

5. В каком случае можно говорить о полюсах функции.

Лекция 5 вычет функции в особой точке. Применение вычетов.

Цель: Изучить применение вычетов функции.

Задачи:

1. Изучить понятие вычета функции.

2. Изучить поведение функции в окрестности изолированной особой точке.

3. изучить применение вычетов.

Вычетом функции в изолированной точкеназывается интеграл вида:

который, берется по замкнутому контуру, охватывающему точку и не содержащему внутри других особых точек и непроходящему через такие точки.

Теорема о вычетах.

Пусть регулярная аналитическая функция внутри контура Г за исключением находящихся внутри Г особых точеки непрерывна на всей области Г. Тогда интеграл по области Г равен сумме вычетов в этих особых точках умноженный на.

Доказательство.

Пусть внутри Г, расположены точки . Окружим каждую точку малым контуромтак, чтобы каждаязаключала внутри себя только одну точкуz, целиком лежащую внутри контура и не пересекается с другими .

По теореме Коши:

в последнем равенстве для каждого интеграла правой части справедливо равенство:

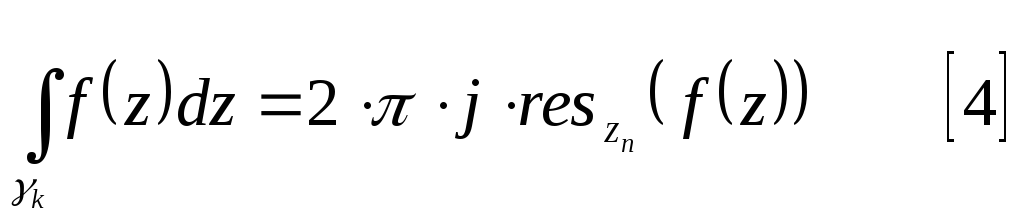
Подставив [4] в [3] получаем [2].

В изолированной особой точке однозначного характера вычет в ней равен коэффициентуряда Лорана функциипри.

Теорема.

Пусть - простой полюс для функции, где- простой ноль для, то есть. Тогда справедливо равенство:

.

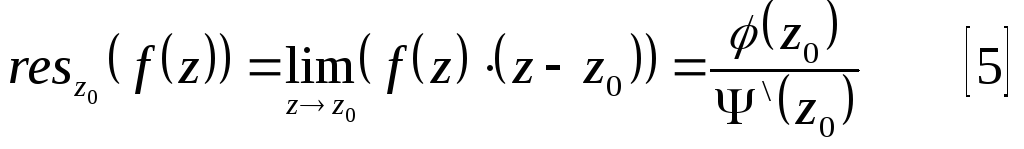Доказательство.

Если - простой полюс, то ряд Лорана дляимеет следующий вид:

Умножая обе части [6] наи переходя к пределу получаем:

так как - простой ноль для функции, а, так как, тогда для предела [7] справедливо равенство:

подставив [8] в [7] получаем [6].

Если - порядкаn, для функции , тогда вычет этой функции в точкебудет иметь следующий вид:

Для вычисления вычета в особой точке имеет место формула:

при этом функцию следует разложить в ряд Лорана.