Частный случай ряда Фурье.

Допустим функция на промежутке является нечетной, тогда:

Интеграл от нечетной функции в симметричных пределах равен нулю.

Допустим функция на промежутке является четной, тогда:

Интеграл от нечетной функции в симметричных пределах равен удвоенному интегралу в пределах, равных половине симметричной области.

Нахождение коэффициентов ряда Фурье от произвольной функции с симметричными пределами.

Допустим функция является четной, тогда интеграл имеет вид:

Если:

Найдем коэффициенты ряда Фурье:

Ряд Фурье для четной функции имеет вид:

Допустим функция является нечетной, тогда интеграл имеет вид:

Найдем коэффициенты ряда Фурье для этого случая:

Ряд Фурье для этого случая имеет вид:

Частные случаи ряда Фурье.

Рассмотрим 4 частных случая ряда Фурье:

1. Непериодическая функция.

Исходную функцию периодически продолжаем вне интервала на всю ось, и функция, получившаяся в этом случае является периодической с периодом , и на интервале она будет полностью совпадать с исходной функцией, следовательно, для нее можно применить разложение в ряд Фурье, рассмотренное ранее Если функция четная, то разложение [1], если нечетная – [2]..

2. Случай половинного промежутка.

Допустим, произвольная функция задана на промежутке . Для того, чтобы разложить эту функцию в ряд Фурье, ее необходимо достроить ее произвольным способом на этом же промежутке. Существует 2 способа построения.

0. построение симметрично оси ОУ.

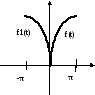
Получим .

будет четной на промежутке , тогда к этой функции можно применить разложение вида:

0. построение симметрично оси ОХ.

Получим .

будет нечетной на промежутке , тогда к этой функции можно применить разложение вида:

3. Случай произвольного промежутка.

, где l – произвольное число. Разложим в ряд Фурье данную функцию. Введем следующую замену:

Тогда разложение будет иметь вид:

, где

Произведя обратную замену и учитывая, что

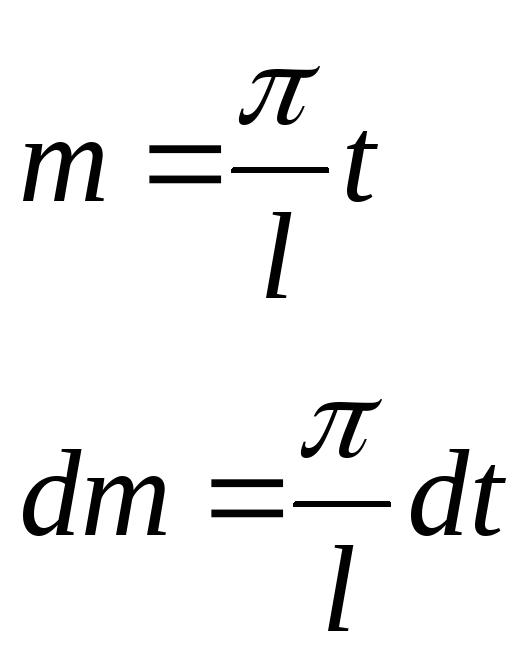
Тогда:

4. Случай произвольного половинного промежутка

Допустим задана на промежутке . Вводи замену:

если t=0, то m=0

если t=l, то m=π.

Тогда справедливо выражение:

Произведя обратную замену :

Комплексная форма ряда Фурье.

Рассмотрим функцию .

Разложим синус и косинус по формуле Эйлера.

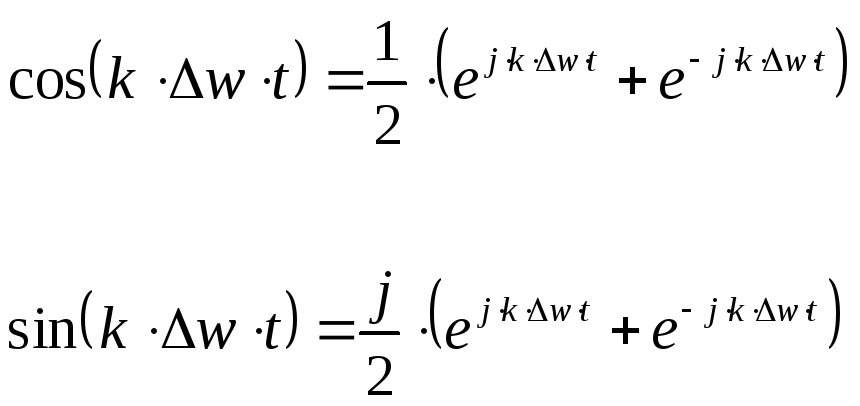
Раскрывая скобки и собирая коэффициенты при иполучаем:

- комплексная форма ряда Фурье.

- комплексные коэффициенты разложения периодической функции в ряд Фурье.

- комплексная гармоника.

Определим :

, где

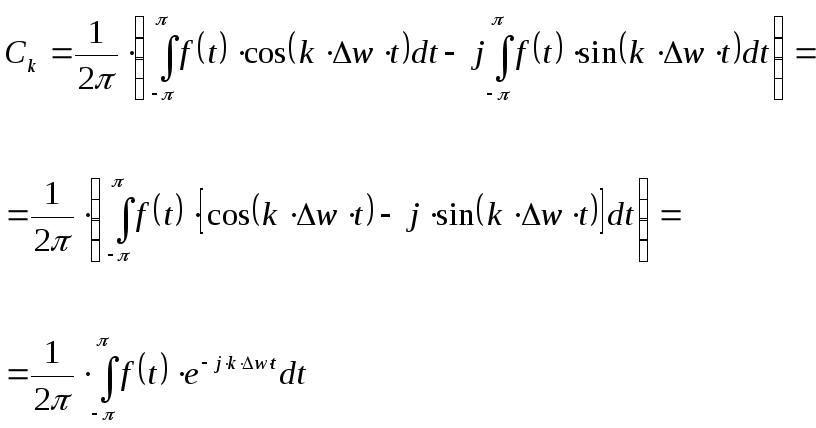
Вопросы для самоконтроля.

1. В каком случае функции являются ортогональными.

2. Как происходит гармонический синтез функции с периодом 2π.

3. Какими выражениями определяются коэффициенты ряда Фурье.

4. Расскажите о частных случаях ряда Фурье.

5. Вывести формулы для определения коэффициентов ряда Фурье на промежутке от 0 до π.

6. Вывести формулы для определения коэффициентов ряда Фурье на промежутке от 0 до l.

7. Вывести формулы для определения коэффициентов ряда Фурье на промежутке от -l до l.

8. Как перейти к комплексной форме ряда Фурье.

Лекция 2

ИНТЕГРАЛ ФУРЬЕ.

Цель. Изучить понятие интеграла Фурье.

Задачи.

1.Изучить интеграл Фурье для функции с периодом 2π.

2. рассмотреть частные случаи интеграла Фурье.

3. Изучить комплексную форму интеграла Фурье.

Допустим функция периодическая и рассмотрим ее на промежутке . При представлении функции в виде ряда Фурье на промежутке , функция периодически продолжается с периодомза пределы интервала. В этом случае получающаяся периодическая функция представляется в виде бесконечной суммы гармоник. Установим, как будет изменяться разложение функции на сумму гармоник, еслиФункция - имеет разложение в ряд Фурье вида:

Коэффициенты для непериодической функции для этого промежутка:

Предположим, что на всей оси t удовлетворяет условию абсолютной интегрируемости:

,

то есть [5] существует.

Подставим [2]-[4] в [1].

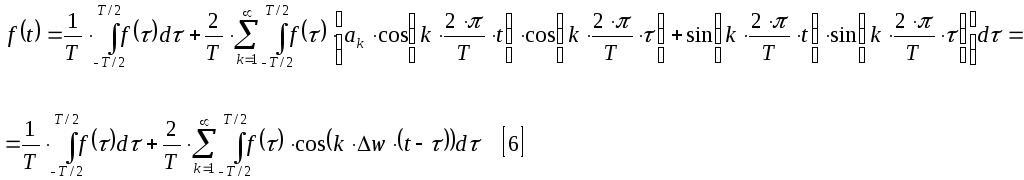
Оценим модуль первого слагаемого ().

при

Оценим второе слагаемое при . Частота первой гармоники. Однако величинаявляется приращением частоты при переходе к совокупности частот гармоникиот одной частоты к соседней. При. приращение частот есть величина очень маленькая и в этом случае приращение частотыможно отождествить с дифференциалом. В этом случае [6] представляет собой:

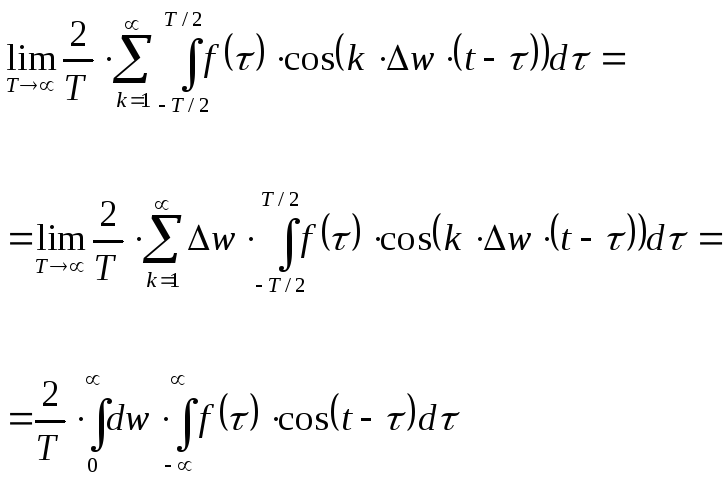
Для непериодической функции:

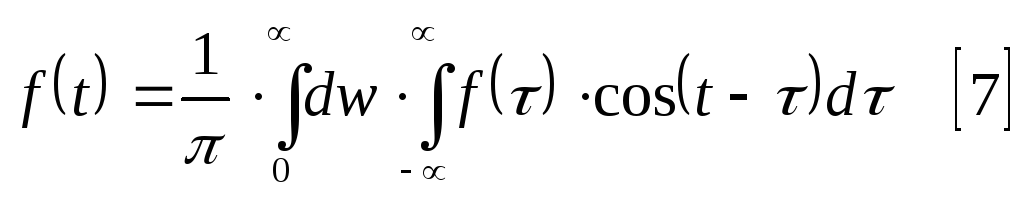- интеграл Фурье.

В полученном выражении распишем косинус разности для нахождения коэффициентов Фурье.

Коэффициенты являются коэффициентами интеграла Фурье и соответственно коэффициентами.