Частный случай интеграла Фурье.

Рассмотри частный случай разложения интеграла Фурье.

- четная:

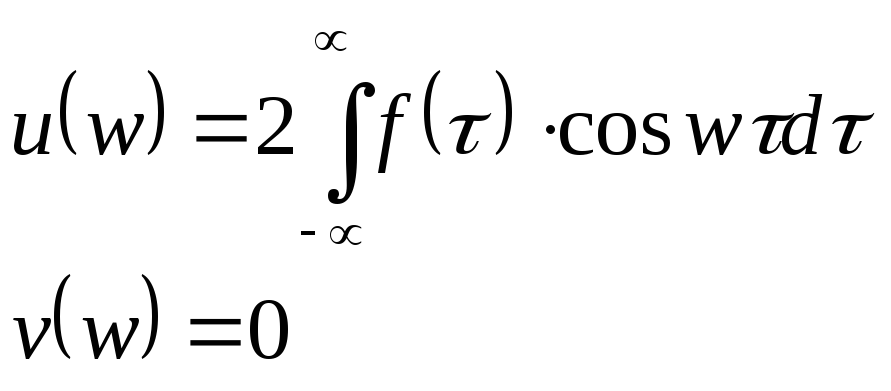
Если - четная, то интеграл Фурье примет вид:

.

- нечетная:

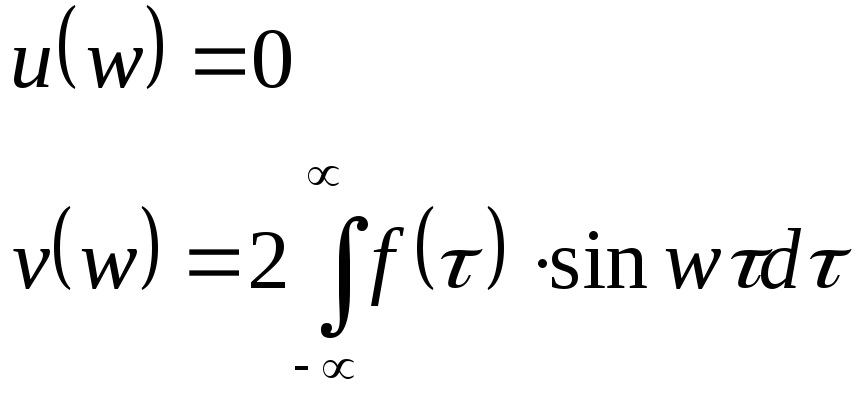
Если - нечетная, то интеграл Фурье примет вид:

.

Формулы [8] и ее частные случаи [9], [10] характеризуют разложение непериодической функции на сумму гармонических составляющих с частотами w и непрерывно изменяющихся на интервале.

Комплексная форма интеграла Фурье.

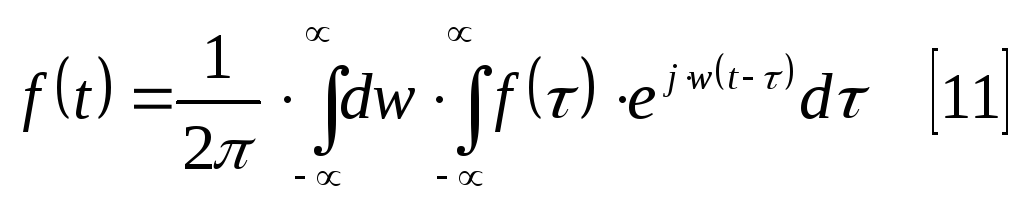
Допустим [11] имеет смысл.

Полученное выражение подставим в [11].

Выражения в круглых скобках в 1 и во 2 слагаемом являются соответственно четной и нечетной функцией относительно w, поэтому.

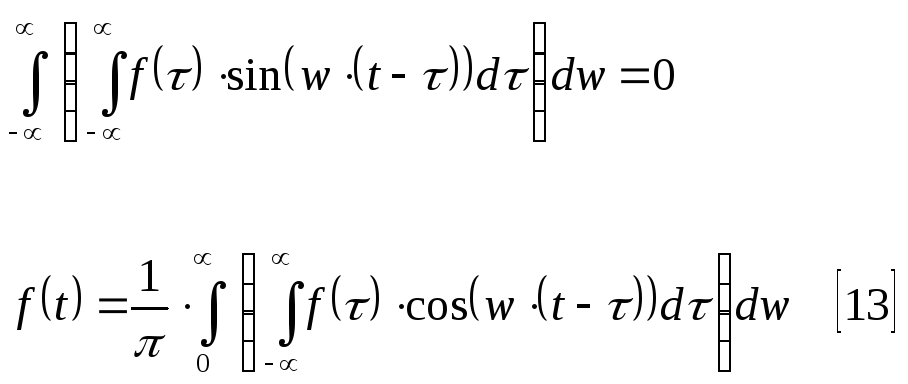
Сравнивая [13] с выражением для интеграла Фурье [7], приходим к выводу, что они идентичны. Следовательно [11] является комплексной формой интеграла Фурье. В [11] множитель не зависит отследовательно можно его вынести из под знака интеграла. Тогда получим:

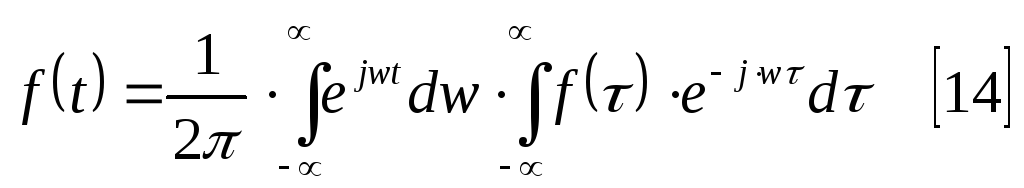
Перейдем от к.

Формула 15 имеет своим аналогом комплексную форму ряда Фурье, и здесь роль коэффициента играет внутренний интеграл Обозначим его как:

Тогда [15] примет вид:

Функция является спектральной плотностью функции.

Вопросы для самоконтроля.

1. какой вид имеет разложение для интеграла Фурье.

2. Какую аналогию можно провести для интеграла с рядом Фурье.

3. Если функция четная, как выглядит для нее интеграл Фурье.

4. Если функция нечетная, как выглядит для нее интеграл Фурье.

5. Какой вид имеет комплексная форма интеграла Фурье.

Лекция 3 спектральный анализ и синтез функции.

Цель. Изучить спектральный состав сигналов.

Задачи:

1. Изучить типы и свойства спектров.

2. Изучить частотные спектры функций.

3. Изучить спектры некоторых типовых сигналов.

4. Изучить понятие спектральной характеристики.

Рассмотрим непрерывные и дискретные спектры.

Совокупность коэффициентов ипри разложении периодической функции в ряд Фурье называются частотными спектрами этой функции.

и являются зависимыми от номера гармоникиk.

Графически частотные спектры изображаются в виде отрезков длины иперпендикулярно оси на которой откладываются значения либо, либо.

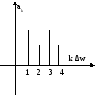
Расстояние между отдельными отрезками равно 1, если , и, если период равен.

Совокупность коэффициентов при комплексном разложении ряда Фурье называется комплексным спектром периодической функции.

Совокупности иназываются амплитудными и фазовыми частотными спектрами периодической функции.

Спектры тоже изображаются в виде отдельных отрезков. При комплексной форме коэффициенты могут быть положительными и отрицательными. В этом случае.

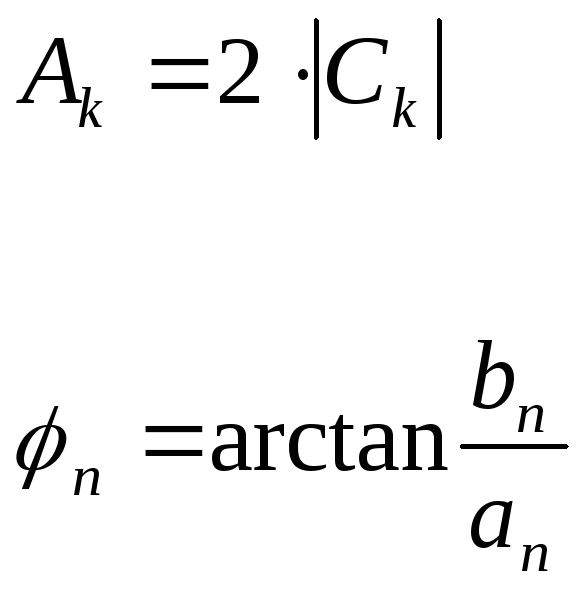
Рассмотрим .

Данное выражение называется спектральной плотностью или спектральной характеристикой периодической функции . Сравним [1] с выражением для комплексной амплитуды-ой гармоники ряда Фурье.

Если . Тогда правые части выражений [1] и [2] совпадают. При этом получим:

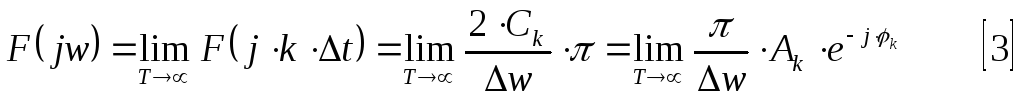
Для при различныхпринимает дискретный ряд значений относительно комплексной амплитуды-ой гармоники при разложении периодической функции. Функцияхарактеризует закон изменения относительной комплексной амплитуды разложение непериодических функций на сумму гармоник, так как частотапри разложении непериодических функций принимает непрерывный ряд значений, то график функциибудет непрерывной кривой.

При разложении непериодической функции в случае, когда разложение будет представлять из себя сумму бесконечного числа гармоник, частота которых будет отличаться друг от друга на бесконечно малую величину. При построении графика амплитудно-частотного спектра непериодических процессов по оси ординат откладывается не амплитуда гармоники А, а относительна амплитуда:

. Если относительная амплитуда используется при построении графика спектра для периодической функции с периодом Т, тогда вместо графика амплитудного спектра получаем график средней плотности амплитуды:

.

В случае при , функцияпредставляет собой спектральную плотность:

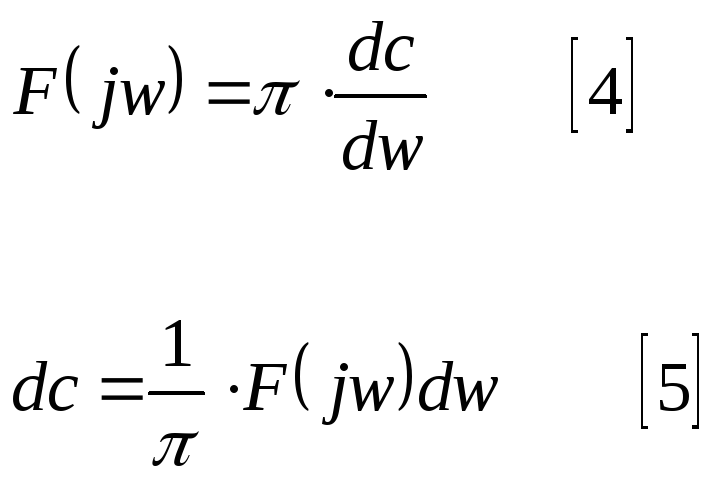
- бесконечно малое приращение амплитуды.

Аргумент спектральной плотности характеризует начальную фазу гармоники, а функция:

- относительную амплитуду этих гармоник.