6.3. Модель управления запасами

Для обеспечения непрерывности производственного процесса необходимо поддерживать разумный запас ресурсов. Если ограничиться случаем, когда все данные детерминированы (достоверно известны), а дефицит ресурса с последующей остановкой производства не допускается, то нужно минимизировать суммарные затраты на приобретение ресурса, на оформление заказа, на хранение заказа. Найти оптимальную стратегию управления запасами – значит решить, когда и в каком количестве пополнять запас ресурса. При записи выражений для функций отдельных затрат необходимо учесть, что:

1. Затраты на приобретение единицы ресурса могут изменяться при изменении как объема, так и времени заказа.

2. Затраты на оформление заказа, как правило, не зависят от объема заказа, но могут зависеть от времени его выполнения.

3. Затраты на хранение заказа включают не только стоимость хранения, содержания и ухода, которые могут изменяться во времени, но и процент на инвестированный капитал.

Если все эти функции, а также потребность в ресурсе не зависят от времени, то модели управления запасами называют статическими. Они относительно просты и позволяют определить как интервал между моментами повторения заказа, так и его оптимальный объем. Если необходимо учесть фактор времени, то используются динамические модели. Применим метод динамического программирования для следующей задачи.

Пусть предстоящий плановый период можно рассматривать как состоящий из n шагов и пусть для каждого i-го шага известна расходуемая величина ресурса . Обозначим ‑ объем запаса на начало шага и ‑ объем заказа, поставляемого перед началом шага. Это искомые переменные, за исключением первоначального запаса ресурса , который должен быть задан, и конечного объема ресурса . На рис. 6.4 эта постановка задачи изображена схематически. Задачу можно решить для любых функций затрат. Для простоты примем, что затраты на хранение на i-м шаге пропорциональны величине запаса, переходящего из шага i на шаг i+1, который будет равен . Эта величина определяет состояние системы на i-м шаге. При записи в таблицы перечня возможных состояний всегда можно считать, что имеющийся запас не должен превышать суммарную потребность на всех последующих шагах, т. е.

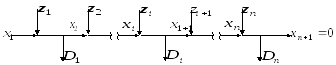
Рис. 6.4

Если для расчета использовать процедуру прямой прогонки (можно применить и обратную прогонку), то рекуррентное уравнение Беллмана приобретет вид:

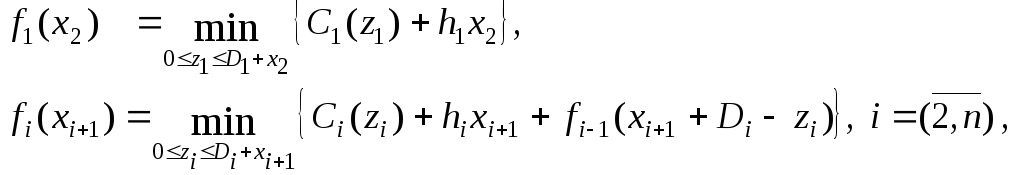
где ‑ минимальные общие затраты на шагах , при условии,

что по завершении i-го шага запас ресурса будет;

‑ затраты на i-м шаге на пополнение ресурса при заказе ;

‑ затраты на хранение единицы продукции, переходящей

с i-го шага на шаг .

Рассмотренная модель применима при любых функциях затрат. Расчет можно упростить, если затраты являются невозрастающими функциями как от объема покупки (например, действуют оптовые скидки), так и при хранении продукции. Для этого случая можно доказать следующие интуитивно очевидные утверждения.

1. Положительный начальный запас можно списать из спроса последующих шагов.

2. При нулевом начальном запасе оптимальная стратегия на любом шаге состоит в удовлетворении спроса за счет или только запаса, или только закупки, но не с обоих источников.

3. Оптимальный объем заказа на любом шаге либо равняется нулю, либо спросу на одном или нескольких последующих шагах.

Проведем расчет для трех шагов при первоначальном запасе ресурса, равном и следующей функции затрат, учитывающей оптовые скидки и затраты на оформление заказа .

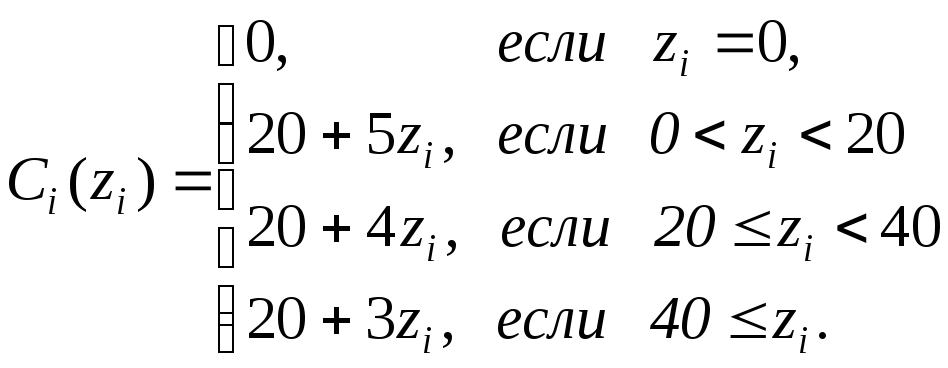
Исходные данные приведены в табл. 6.3.

Таблица 6.3

Шаг, i	Потребность,	Затраты на хранение единицы ресурса,
1	20	2
2	35	1
3	25	1

Таблица 6.4

Шаг 1					Оптимальное решение
			45	70
			155	230
0	0	70	–	–	70	10
35	70	–	225	–	225	45
60	120	–	–	350	350	70
Заказ на шаге 1 для шагов		1	1, 2	1, 2, 3

Можно считать, что запаса нет, а потребность на первом шаге составляет только 10 единиц. Возможные состояния (с учетом потребности в ресурсе на последующих шагах) приведены в табл. 6.4 – 6.6.

Таблица 6.5

Шаг 2					Оптимальное решение
			35	60
			160	200
0	0	0+225=225	160+70=230	–	225	0
25	25	25+350=375	–	225+70=295	295	60
Заказ на шаге 2 для шагов		–	2	2, 3

Таблица 6.6

Шаг 3				Оптимальное решение
			25
			120
0	0	0+295=295	120+225=345	295	0
Заказ на шаге 3 для шагов		–	3

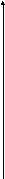
60

350

35

25

225

25

225

10

70

0

0

0

0

0

140

100

шаг 1

шаг 2

шаг 3

Рис. 6.5

Следовательно, минимум суммарных затрат, 295 ед. обеспечивает оптимальная стратегия , , . На рис. 6.5 показаны возможные состояния после каждого шага и затраты на переход от одного состояния к другому с учетом стоимости хранения ресурса. При представлении этой задачи в виде сетевой модели оптимальной стратегией является кратчайший маршрут.

83