2. Основные свойства неопределенного интеграла

Из определения неопределенного интеграла непосредственно вытекают следующие его свойства:

1. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению:

.

2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

.

2. Постоянный множитель можно выносить за знак неопределенного интеграла:

(c – const, ).

2. Неопределенный интеграл от алгебраической суммы непрерывных функций равен алгебраической сумме неопределенных интегралов:

.

Заметим, что свойство 4 справедливо для любого конечного числа слагаемых.

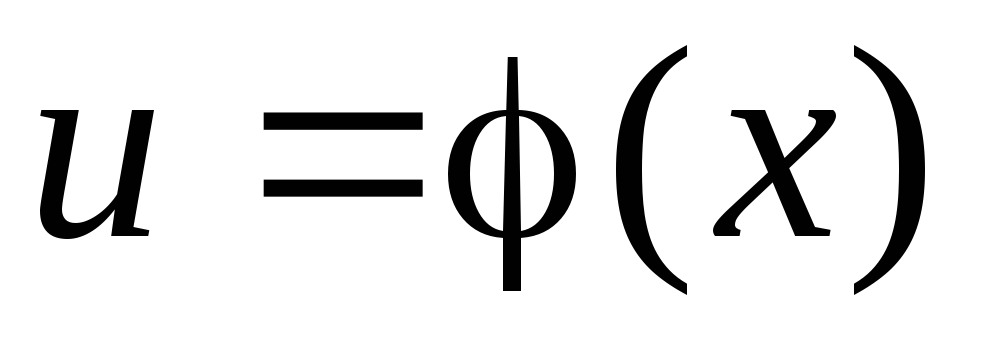2. Если , а – произвольная функция, имеющая непрерывную производную, то.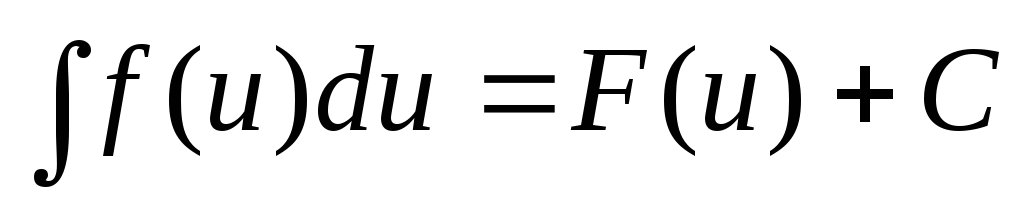

3. Таблица основных неопределенных интегралов

Данную таблицу можно получить, пользуясь тем, что интегрирование есть операция, противоположная дифференцированию. Часть формул этой таблицы непосредственно следует из таблицы производных основных элементарных функций. Справедливость остальных формул легко проверяется дифференцированием.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

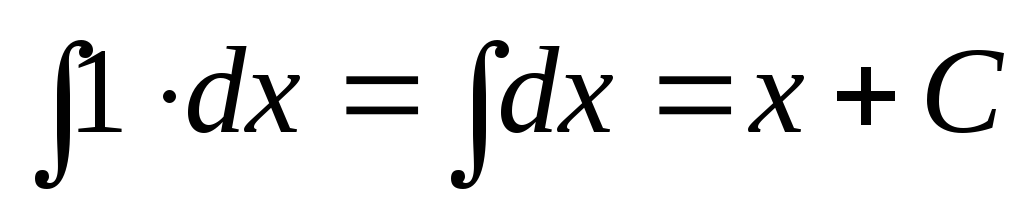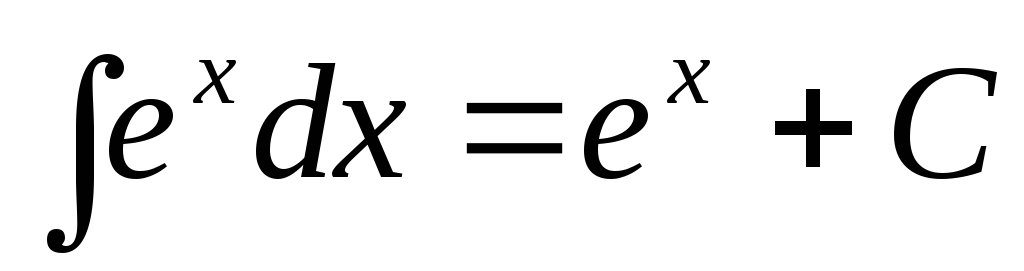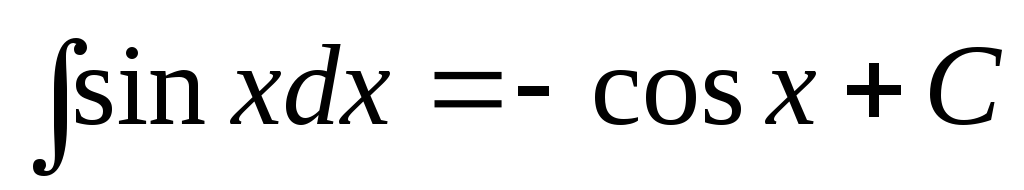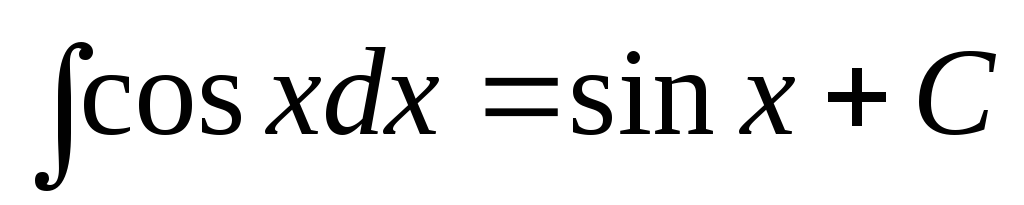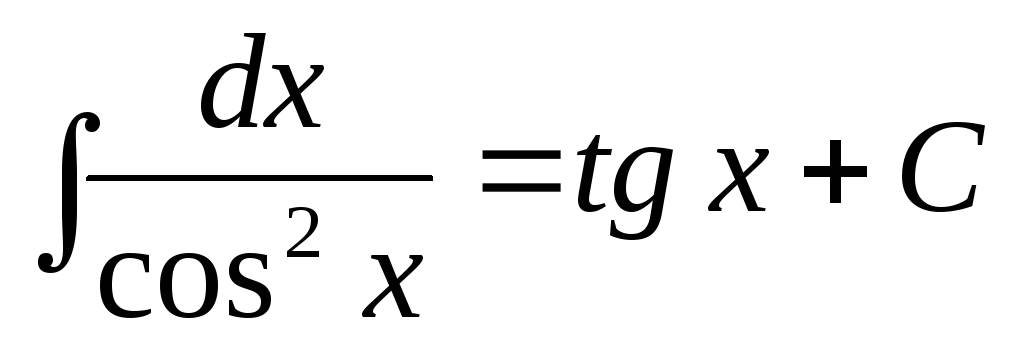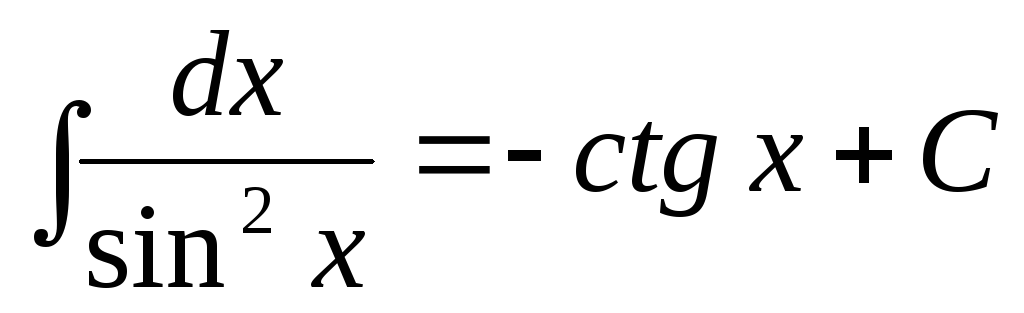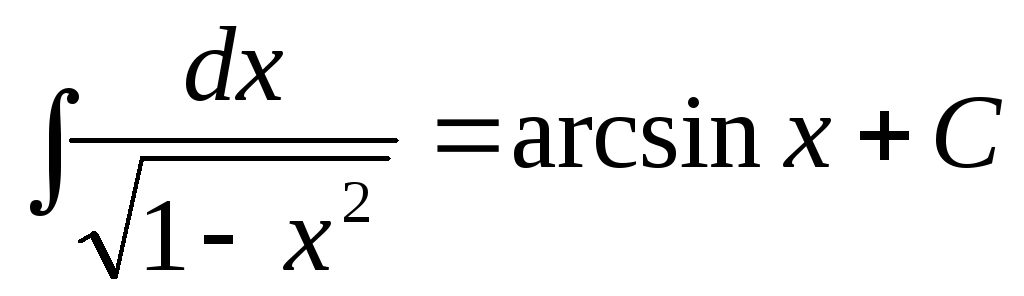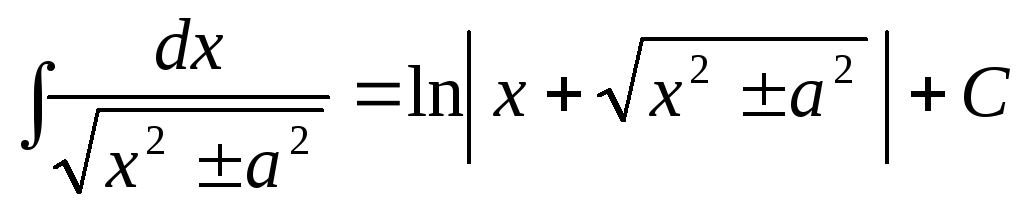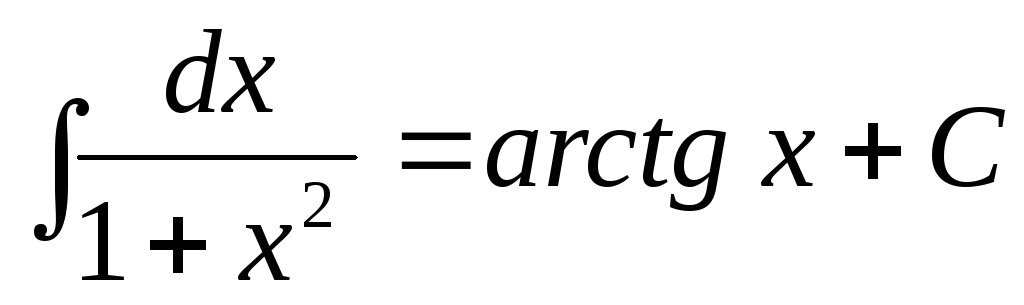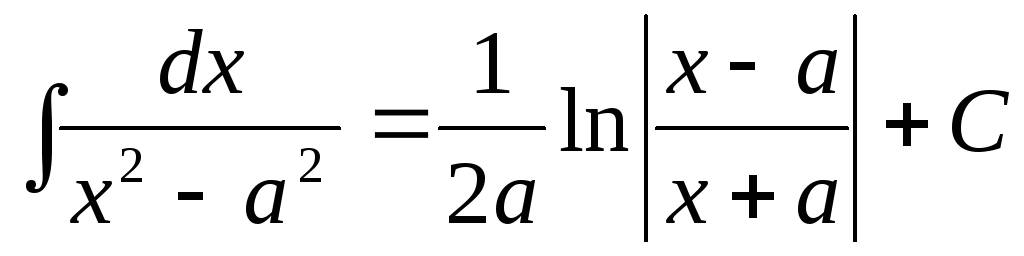В данной таблице переменная интегрирования х может быть как независимой переменной, так и функцией от независимой переменной (см. свойство 5). Например, если в формуле 7 вместо переменной х взять функцию , то получим:

.

Интегралы, содержащиеся в этой таблице, называются табличными. Их необходимо знать наизусть, так как более сложные интегралы сводятся к табличным путем преобразований подынтегральной функции.

4. Основные методы интегрирования

А. Непосредственное интегрирование. Этот метод заключается в непосредственном применении таблицы неопределенных интегралов и свойств 1 - 5 неопределенного интеграла. Иногда требуется предварительное преобразование подынтегральной функции.

При непосредственном вычислении неопределенных интегралов часто используются следующие преобразования дифференциала (операция «под-несения под знак дифференциала»):

,

,

,

,

,

,

,

.

В общем случае: .

Пример 2. Найти интеграл .

Решение. Воспользуемся свойствами 3 и 4 неопределенного интеграла:

.

Находим каждый из полученных табличных интегралов, используя соответственно формулы 3, 4, 5, 7, 2, 12:

; ; ; ; .

В результате имеем:

.

Обозначив , окончательно получим

.

Правильность полученного результата проверим дифференцированием:

. Получили подын-тегральную функцию. Значит, интеграл найден правильно.

Пример 3. Найти интеграл .

Решение. Для нахождения данного интеграла воспользуемся свойством 5 неопределенного интеграла. Так как , то

.

Пример 4. Найти интеграл .

Решение. Преобразуем подынтегральную функцию:

[делим почленно числитель на знаменатель] =

=. Тогда исходный интеграл примет вид

.

Пример 5. Найти интеграл .

Решение. Интеграл не табличный, поэтому преобразуем его, воспользовавшись основным тригонометрическим тождеством . Получим

.

B. Метод замены переменной (подстановки). Непосредственно вычислить интегралы с помощью таблицы неопределенных интегралов и свойств 1 - 5 удается довольно редко. Поэтому для вычисления неопределенных интегралов используют другие методы, среди которых одним из важнейших является метод замены переменной (или метод подстановки). Суть этого метода заключается во введении новой переменной интегрирования. При этом исходный интеграл сводится к новому интегралу, который либо является табличным, либо легко к нему сводится путем преобразований подынтегральной функции.

Пусть требуется вычислить интеграл , который не вычисляется непосредственно. Сделаем замену переменной , где – дифференцируемая функция. Тогда и исходный интеграл приобретет вид

. (1)

Формула (1) называется формулой замены переменной в неопределенном интеграле. После вычисления интеграла в правой части этого равенства следует перейти от новой переменной интегрирования к старой переменной .

Формулу (1) можно применять и в обратном порядке, т.е. справа налево. В этом случае используют подстановку , тогда =.

Пример 6. Найти интеграл .

Решение. Сделаем замену , тогда , а . Найдем : . Следовательно, = . Возвращаясь к переменной , окончательно получаем: .

Заметим, что данный интеграл можно было вычислить непосредственно, воспользовавшись следующим преобразованием дифференциала: . (Сделать самостоятельно).

Пример 7. Найти интеграл .

Решение. Полагаем . Отсюда находим . Следовательно:

.

Пример 8. Найти интеграл .

Решение. Положим , тогда , , . Таким образом:

.

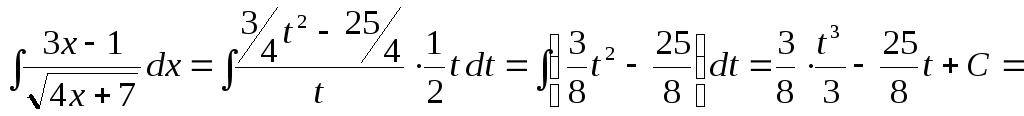
Пример 9. Найти интеграл .

Решение. Пусть , тогда . Из последнего равенства выразим произведение , входящее в подынтегральное выражение: . Следовательно:

.

При вычислении интегралов необходимо помнить следующее правило: если числитель подынтегральной функции f(x) равен производной знаменателя, то справедлива формула

, (2)

или

. (3)

Пример 10. Найти интеграл .

Решение. Так как , то исходный интеграл можно записать в виде . Замечая, что , по формуле (2) получим .

В заключение заметим, что общих методов выбора подстановки не существует. Умение правильно определить подстановку приобретается практикой и базируется на твердых знаниях табличных интегралов и хорошем владении техникой дифференцирования.

С. Метод интегрирования по частям. Пусть и – две дифференцируемые функции. По свойству дифференциала

,

или

.

Интегрируя обе части последнего равенства и учитывая, что , получаем

. (4)

Формула (4) называется формулой интегрирования по частям. Метод интегрирования по частям состоит в том, что подынтегральное выражение представляется в виде произведения двух сомножителей и ; в качестве u обычно выбирается функция, которая при дифференцировании упрощается, в качестве dv – оставшаяся часть подынтегрального выражения, содержащая dx, из которой путем интегрирования можно определить функцию . Затем, после нахождения и , используют формулу (4).

В некоторых случаях для нахождения искомого интеграла формулу интегрирования по частям приходится применять несколько раз.

Большая часть интегралов, берущихся по формуле (4), может быть разбита на три группы:

1. К первой группе относятся интегралы вида

, , , , , ,

где – многочлен. Для их вычисления следует применить формулу (4), полагая в ней равным одной из указанных выше функций, а .

2. Ко второй группе относятся интегралы вида

, , ,

где – многочлен; – некоторое число. Для их вычисления следует положить , а , , соответственно.

3. К третьей группе относятся интегралы вида

, , , ,

где и – некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям, причем за можно принимать любой из сомножителей. В результате получим уравнение первого порядка относительно исходного интеграла.

Пример 11. Найти интеграл .

Решение. Данный интеграл относится к первой группе, поэтому полагаем , . Тогда , , (при нахождении постоянную можно положить равной нулю). Применяя формулу (4), получаем

=

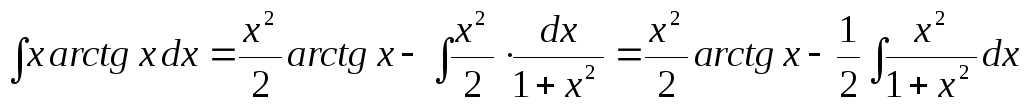= [интеграл был вычислен ранее (см. пример 4)] =

, где .

Пример 12. Найти интеграл .

Решение. Положим . Тогда , . По формуле (4) получаем

.

Интеграл в правой части полученного равенства не является табличным, но он значительно проще исходного, так как степень переменной в подынтегральном выражении уменьшилась на единицу, в то же время второй сомножитель того же типа, что и в исходном интеграле. Для вычисления интеграла еще раз применим формулу (4), полагая на этот раз . Получим , . Следовательно:

.

Пример 13. Найти интеграл .

Решение. Пусть . Тогда , = . Применяя формулу интегрирования по частям, получим . Последний интеграл снова вычисляем интегрированием по частям, положив , откуда найдем . Тогда

.

Перенося интеграл из правой части полученного равенства в левую, получаем

.

Следовательно,

.