3. Интегрирование простейших иррациональных функций

1. Интегралы вида , где – рациональная функция; – целые числа, находятся с помощью подстановки , где – наименьшее общее кратное чисел (т.е. n = НОК()).

Пример 5. Вычислить интеграл .

Решение. Данный интеграл можно записать в виде =. Имеем: , следовательно НОК. Поэтому полагаем , . Получим [аналогичный интеграл вычислен в примере 4 лекции 1] = +

[возвращаемся к переменной х: ] = .

2. Интегралы вида

, где – рациональная функция; – целые числа, приводятся к интегралам от рациональных функций с помощью подстановки , где – наименьшее общее кратное чисел .

Пример 6. Вычислить интеграл .

Решение. 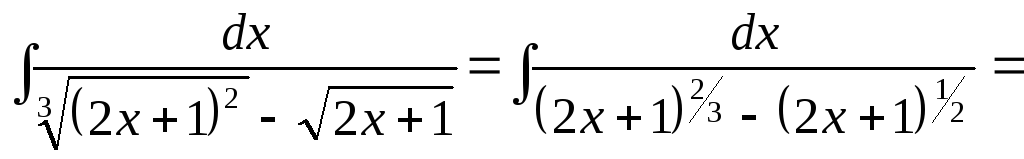[в данном случае , следовательно, НОК и откуда ] = [для вычисления последнего интеграла в числителе дроби вычтем и прибавим единицу, а затем разделим почленно числитель на знаменатель] = [первый из полученных интегралов разобьем на два, а второй вычислим, воспользовавшись преобразованием дифференциала ] = [так как ] = .

4. Интегрирование тригонометрических функций

1. Интегралы вида 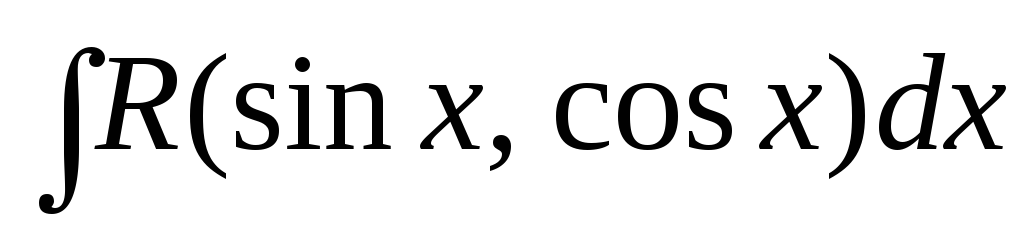, где R – рациональная функция от и , приводятся к интегралам от рациональных функций с помощью подстановки 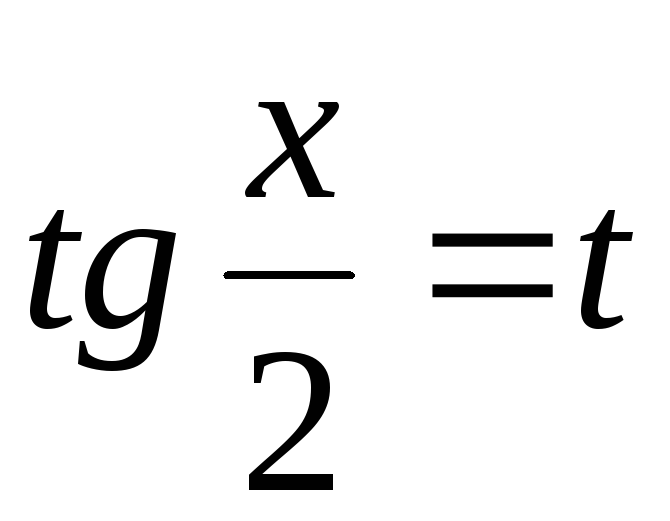(универсальная тригонометрическая подстановка).

Действительно, 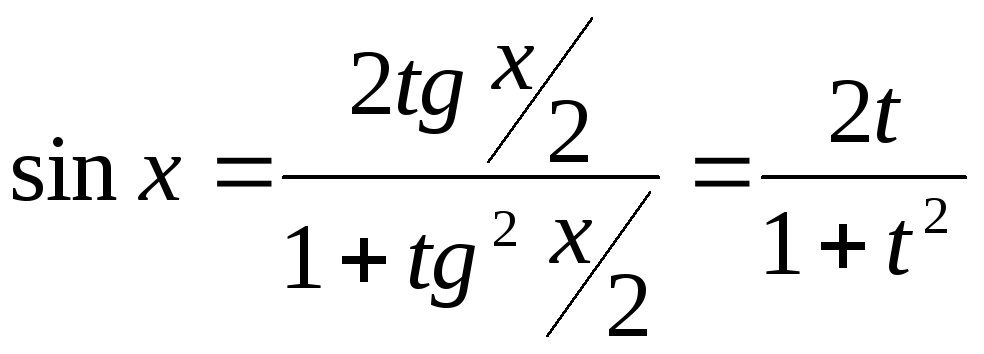, , , . Тогда

,

где – рациональная функция от переменной .

Пример 7. Вычислить интеграл .

Решение. Положим . Тогда , , . Следовательно:

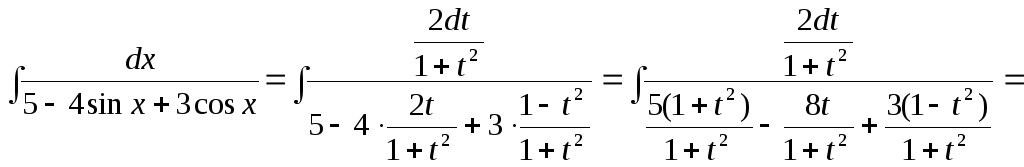
[переходя к переменной x] =.

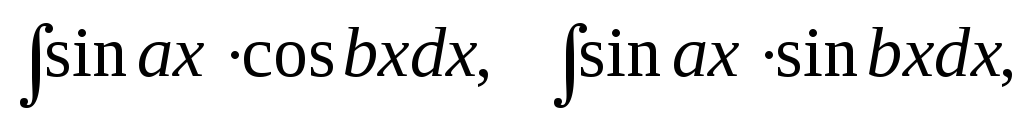
2. Интегралы вида 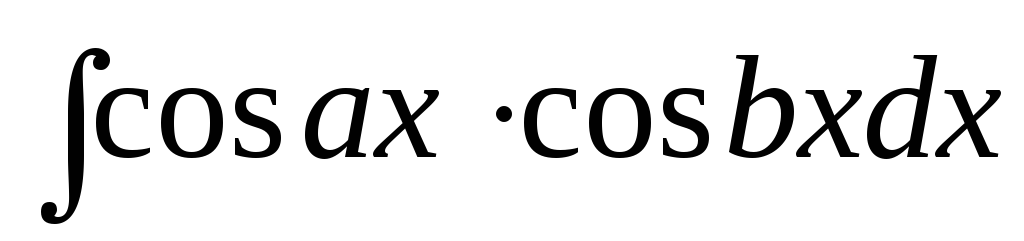находятся с помощью тригонометрических формул:

.

Пример 8. Найти интеграл .

Решение. Так как

, то

.

3. Интегралы вида 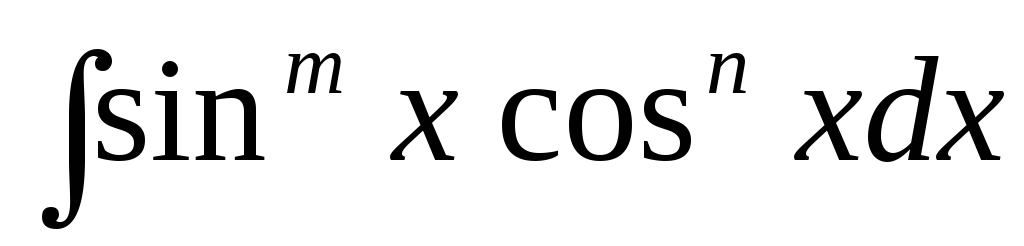, где и – четные числа, находятся с помощью формул:

; .

Если одно из чисел или – нечетное или оба этих числа – нечетные, то интеграл вычисляется непосредственно, путем отделения от нечетной степени одного множителя и введения новой переменной: , если – нечетное; , если – нечетное.

Пример 9. Найти интеграл .

Решение.

.

Пример 10. Найти интеграл .

Решение.

[так как ] = =[замена ] = =.

Задачи и упражнения

1. Найти интегралы:

a) ; б) ; в) ;

г) ; д) ; е) ;

ж) ; з) ; и) ;

к) ; л) ; м) .

2. Найти интегралы:

а) ; б) ; в) ;

г) ; д) ; е) .

2. Найти интегралы:

а) ; б) ; в) ;

г) ; д) е)

ж) з) ; и)

к) ; л) .

Литература

1. Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I. – М.: Наука, 1982. – 616 с.

2. Гусак А. А. Математический анализ и дифференциальные уравне-ния.– Мн.: ТетраСистемс, 1998. – 416 с.

3. Гусак А. А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).

4. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.

5. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000. – 351 с.