3.6.3. Перевірка існування автокореляції

З попереднього параграфа випливає, що для встановлення відповідності між отриманою моделлю, що задається рівнянням регресії з оціненими за М.Н.К. його коефіцієнтами, і справжньою залежністю обов'язковою є перевірка автокореляції залишків. При перевірці автокореляції досліджується гіпотеза про те, що залишки u_j, j = 1; 2; ... ; m, неавтокорельовані, тобто їхня коваріаційна матриця діагональна. Коефіцієнт автокореляції  поміж послідовними значеннями u_j повинен дорівнювати нулю. Нульова гіпотеза у цьому випадку, Н₀:  = 0

Якщо Н₀ не виконується, то

1) >0 (позитивна автокореляція);

2) <0 (негативна автокореляція).

Дарбін і Уотсон запропонували для вибірок малого обсягу (m<30) оцінку  d - статистику

(3.37 )

Її закон розподілу вони досліджували для фіксованого m за наступних умов:

1) залишки u_j розподілені нормально;

2) у оцінюваній лінії регресії міститься постійний член а₀, тобто ;

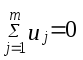3) фактори x_j невипадкові величини.

Можна показати [2], що 0<d<4, причому при повній позитивній автокореляції d=0, при негативної d=4, а при d=2 відсутня автокореляція залишків. Для d-статистики знайдені критичні межі, що дозволяють прийняти або відхилити гіпотезу Н₀ для рівня значимості.

Позначимо нижню критичну межу d через d_L, а верхню через d_v. Значення d_L і d_v залежать від числа вимірів (числа досвідів) m і від числа факторів x_i, рівного n. Якщо обчислене за (3.37) d менше 2, причому 0<d<d_L, тo залишки u_j позитивно корельовані, основна гіпотеза (=0) відхиляється. Якщо d_v<d<2 - залишки некорельовані. Якщо d_L<d<d_v, то відповідь не визначена, для одержання однозначної відповіді треба збільшити число вимірів m.

У випадку, коли d>2, досліджується на наявність негативної автокореляції залишків. Якщо 2<d<4-d_v, то з надійністю 1- немає підстав відхилити гіпотезу про відсутність автокореляції залишків. Якщо 4-d_v<d<4-d, то вимагаються додаткові дослідження. Якщо 4-d_L<d<4 то у наявності негативна автокореляція залишків. Величина d_L, d_v наведені у таблиці для рівня значимості = 0,05

Таблиця 1

Критичні значення d_L, d_v для статистики d

Число спо	Число факторів рівнянь
стережень	n=1		n=2		n=3		n=4		n=5
	dL	dv	dL	dv	dL	dv	dL	dv	dL	dv
15	1,08	1,36	0,95	1,54	0,82	1,75	0,69	1,97	0,56	2,21
20	1,20	1,41	1,1	1,54	1,00	1,68	0,9	1,83	0,79	1,99
25	1,29	1,45	1,21	1,55	1,12	1,66	1,04	1,77	0,95	1,89
30	1,35	1,49	1,28	1,57	1,21	1,65	1,14	1,74	1,07	1,83

Якщо критерій Дарбіна-Уотсона не дає відповіді на питання про автокореляцію залишків, то можна застосувати критерій фон Неймана [5] із його статистикою

Q = (3.38)

Треба зауважити, що цей критерій правомірно застосовується для великих m. Але на відміну від першого критерію він дає однозначну відповідь на питання про автокореляцію залишків і тому з натяжкою можна намагатися його застосовувати у розглянутому випадку.