3.3. Стандартна похибка моделі й залежної змінної

Після одержання моделі залежності у вигляді регресійного рівняння знаходиться стандартна виправлена помилка цього рівняння , де , вибіркова дисперсія, що є оцінкою (пункт б). Позначимо . Тоді

= (3.9)

à невиправлена дисперсія без врахування числа ступенів свободи

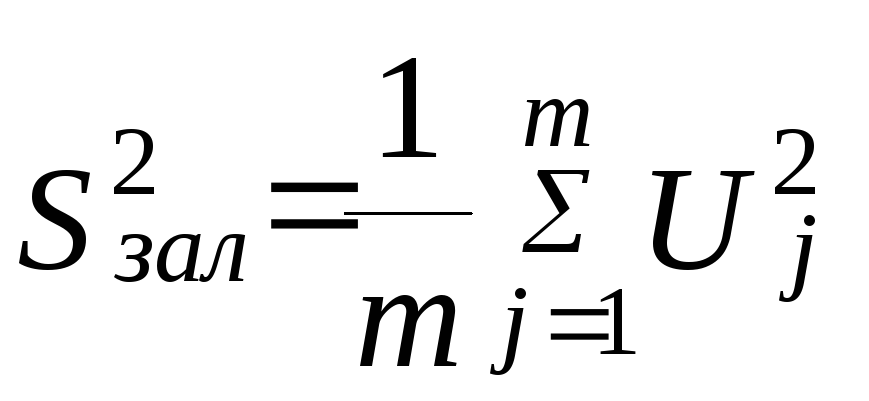(3.10 )

Стандартна (середня квадратична) помилка залежної перемінної у з поправкою на число ступенів свободи відрізняється від (2.13)

(3.11 )

3.4. Коефіцієнти детермінації і множинної кореляції

Коефіцієнт детермінації D, як і стандартні помилки, обчислюється з поправкою на число ступенів свободи і без неї. Коефіцієнт детермінації без поправки

, (3.12 )

Це відношення показує, яка частина руху залежної перемінної у описується отриманим рівнянням регресії. Величина R= називається множинним коефіцієнтом кореляції.

Коефіцієнти детермінації і множинної кореляції з урахуванням числа ступенів свободи обчислюються за формулами:

, (3.13 )

Можна довести, що . (3.14)

Виправлений коефіцієнт множинної кореляції .

Обчислимо D іншим способом. У наших позначеннях , де , або у матричній формі . Тому, що за М.Н.К. формула (2.8) , то

Тоді ;

, (3.15 )

Якщо перейти до нормалізованих перемінних за формулами (2.12), то у нових позначеннях (див. (2.18)).

Тоді

(3.16)

Коефіцієнти множинної кореляції R виражають міру зв'язку залежної перемінної з усіма незалежними факторами. Максимальне його значення дорівнює 1. Величина 1 - R² характеризує ступінь впливу на залежну перемінну випадкових залишків.

Статистична значимість коефіцієнта детермінації перевіряється за допомогою F-критерію. Обчислюється розрахункове значення критерію за формулою:

(3.17 )

Якщо F_p>F_кр (; n; m-n-1), де F_кр - табличне значення для рівня значущості і числа ступенів свободи n і m-n-1, то коефіцієнт детермінації вважається значущим із довірчою ймовірністю р=1-, у противному випадку, при F_p<F_кр, - незначущим.

Значущість відмінності від нуля D означає також і значущість коефіцієнту R.

3.5. Стандартні похибки параметрів

Статистичну значущість оцінених параметрів (коефіцієнтів) регресійного рівняння (моделі) перевіряють за допомогою стандартних похибок параметрів. Внесок кожної незалежної перемінної у дисперсію показника y визначається за допомогою - коефіцієнтів, що обчислюються за формулою (2.19). Це випливає з (2.14). Для перевірки значущості оцінок параметрів _k, обумовлених за (2.15), знаходиться їх коваріаційна матриця

. (3.18 )

Ця матриця має розмірність (n+1)(n+1), тому що враховує і дисперсію ₀. Тоді стандартна помилка параметра _i, , де S_ii - діагональний елемент матриці .

Статистична значущість параметрів _i перевіряється за допомогою t-критерію. Для цього обчислюються розрахункові значення критерію для _i.

(3.19 )

Якщо t_p>t_кр (; m-n-1), де t_kp - табличне значення t - розподілення для рівня значущості і числа ступенів свободи m-n-1, то _i - суттєво відрізняється від нуля, тобто вплив фактора х_i на y істотний, якщо t_p < t_kp, то несуттєво. У такому випадку фактори х_i можна виключити з моделі. Якщо вибіркові коефіцієнти кореляції між факторами незначні, то за величинами можна проранжувати фактори за їх силою впливу на y. Тому краще перевіряти істотність впливу факторів х_i на y як значущість - коефіцієнтів за тією самою методикою, що й _i. Тоді

(3.20 )

(3.21)

де , C_ii - діагональний елемент R-1.

При побудові довірчих інтервалів для параметрів _i використовується той факт [4], що величина задовольняє t - розподілу з m-n-1 ступенями свободи. Тому з надійністю 1- довірчий інтервал для а_i задається як

(3.22 )

Для стандартизованого рівняння довірчі інтервали для _i- коефіцієнтів

(3.23 )

де С_ii i-ий діагональний елемент матриці R-1.