7.6. Метод наискорейшего спуска

С целью уменьшения общего количества итераций применяют градиентный метод с переменным шагом (дроблением шага). Этот метод называют методом наискорейшего спуска. В градиентном методе наискорейшего спуска первоначальный шаг выбирается достаточно большим, а затем его величина уменьшается в соответствии с определенным правилом, например, методом деления отрезка пополам. Величина шага на каждой итерации связана с поведением функции в окрестности очередной точки последовательности.

В методе наискорейшего спуска движение предполагается по градиенту с оптимальной, т. е. по возможности наибольшей величиной шага на каждой итерации, исходя из условия экстремума целевой функции в направлении градиента

. (7.21)

На каждой итерации необходимо решать задачу оптимизации целевой функции как одномерной функции величины шага

. (7.22)

Значение h, при котором достигается минимум функции , принимается за величину оптимального шага . При поиске минимума целевой функции в формулах (7.9) и (7.22) ставится минус и плюс - в случае нахождения максимума функции.

Решение задачи оптимизации функции может выполняться любыми методами.

Если функция дифференцируема, то искомым значением будет корень уравнения .

Геометрический смысл метода наискорейшего спуска:

Рассмотрим ,

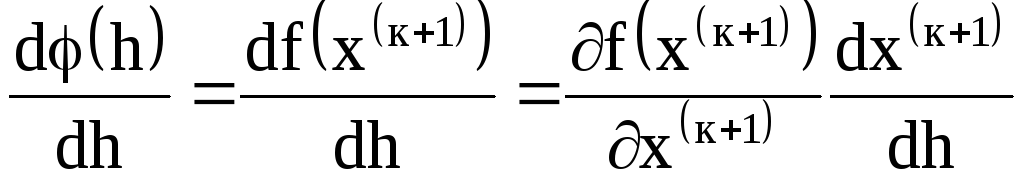и ,

то .

Следовательно,

. (7.23)

Так как , то градиенты целевой функции в двух соседних точках итерационной последовательности взаимно ортогональны. Поэтому траектория поиска представляет последовательность ортогональных друг к другу отрезков прямых (Рис. 7.5).

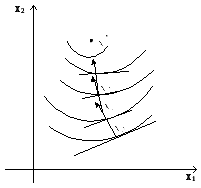
Рис.7.5. Траектория поиска экстремума

Пример. Найти максимум функции в условиях предыдущего примера методом наискорейшего спуска.

Результаты вычислений представлены в расчетной таблице 7.2.

Таблица 7.2

Расчетная таблица

к
0	0	0	2	12	12,17	3+148h-292	148-584h=0	0,25
1	0,5	3,0	1	0	1,0	21,75+h-	1-2h=0	0,5
2	1,0	3,0	0	0	0			-

Уже на второй итерации получен результат. Пояснение для первой строки расчетной таблицы 7.2:

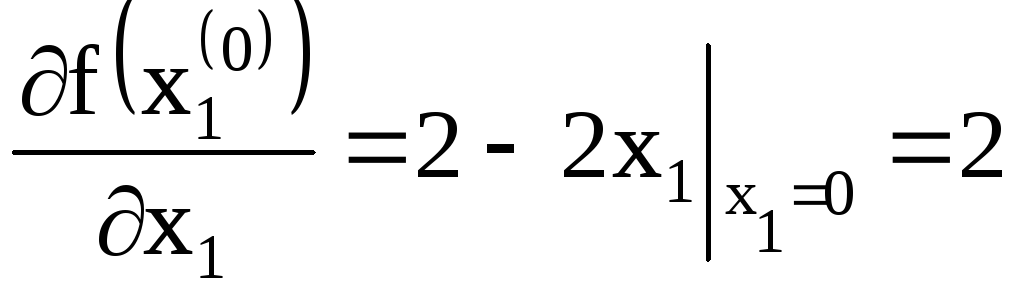
1-й шаг: Начальная точка . Для целевой функции =3+2 находим ; 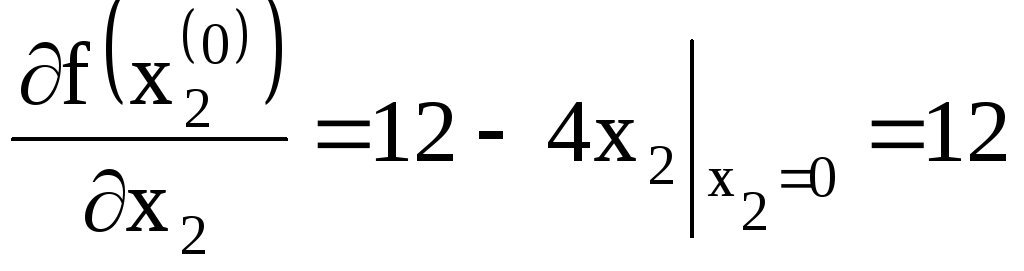,17;

и ;

.

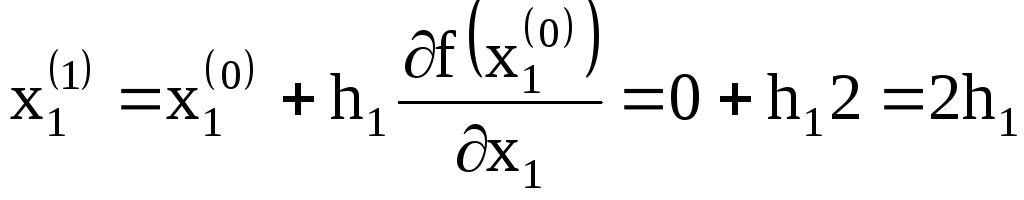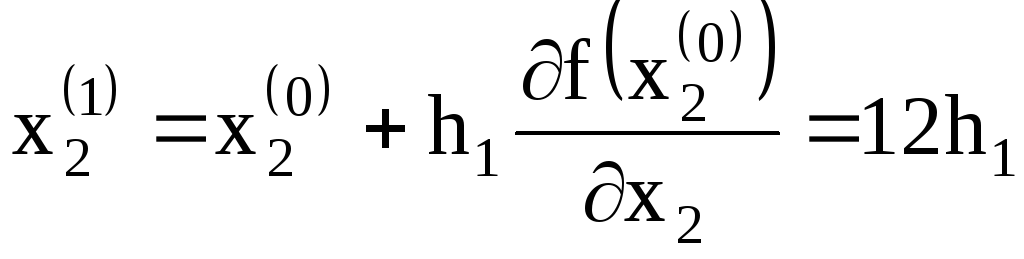Подставим полученные значения в уравнение целевой функции . Находим и . и т.д.

Модификация метода скорейшего спуска

Решается задача минимизации функции .

Задаем координаты начальной точки и находим градиент (используется разностное приближение производной).

Выбираем шаг h, затем переходим в направлении антиградиента в новую точку, выбираем шаг h₁ (используется метод деления отрезка пополам).

Чтобы избежать зацикливания программы, в нее вставлен счетчик циклов Т, когда Т > , счет оканчивается (высвечивается “ Время ”); счет также заканчивается, когда сумма абсолютных величин производных меньше заданного положительного числа ..