7.3. Градиентные методы

Пусть задача нелинейного программирования состоит в минимизации функции , т.е. в отыскании вектора , который доставляет этой функции глобальный минимум.

Функция называется целевой функцией или функцией цели.

Если функция дифференцируема в точке , то градиентом в точке называется n-мерный вектор

.

Градиент в каждой точке , в которой он существует, направлен по нормали к линии уровня поверхности и показывает направление наискорейшего возрастания функции в данной точке (рис 7.2)

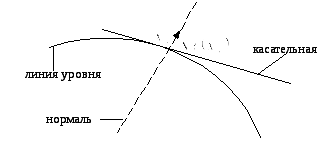
Рис. 7.2. Свойства вектора градиента

Если градиент отличен от нуля, то он указывает направление наибыстрейшего роста значения функции .

Вектор «-», противоположный градиенту, называется антиградиентом и указывает направление наискорейшего убывания функции .

Для выпуклой функции необходимым и достаточным условием оптимальности точки является равенство нулю градиента функции в этой точке, т. е. .

Алгоритм градиентного метода

Идея градиентного метода: если заранее известно, что функция имеет в допустимой области единственный экстремум, то поиск точки, в которой он достигается, целесообразнее проводить следующим образом. В допустимой области взять производную функции в точке и с помощью градиента (антиградиента) определить направление, в котором целевая функция возрастает (убывает) с наибольшей скоростью.

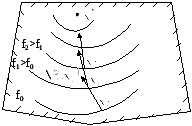
Рис.7.3. Поиск экстремума градиентным методом

Сделав наибольший шаг в найденном направлении, перейти в новую точку . Потом снова определить наилучшее направление для перехода в очередную точку и т. д., иначе говоря, надо построить последовательность точек так, чтобы она сходилась в точке экстремума , т.е. для точек последовательности выполнялись условия

Величина шага из точки по направлению градиента (антиградиента -) определяется значением параметра в уравнении прямой

, (7.9)

Методы поиска экстремума, основанные на построении последовательности точек , называют шаговыми или итерационными. Эти методы различаются способом выбора направления движения и способом выбора шага , от этого зависит сходимость методов.

Большое значение имеет также выбор начальной точки .

В качестве критериев прекращения итерационного процесса, свидетельствующих о достижении достаточной близости последней точки последовательности к точке экстремума , могут использоваться или модуль градиента

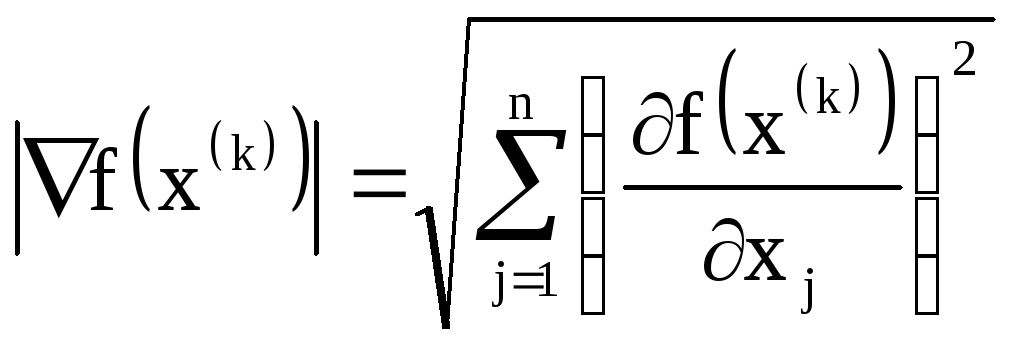, (7.10)

или модуль разности оптимизируемой функции в двух соседних точках последовательности.

Значения критериев сравниваются с достаточно малыми положительными числами , соответствующими требуемой точности решения.

Признаком прекращения итерационного процесса служит выполнение неравенства

. (7.11)

Используя градиентные методы, можно найти решение любой задачи нелинейного программирования. Однако в общем случае применение этих методов позволяет найти точку локального экстремума. Поэтому более целесообразно использовать градиентные методы для нахождения решения задач выпуклого программирования, в которых всякий экстремум является одновременно и глобальным. Процесс нахождения решения задачи с помощью градиентных методов состоит в том, что, начиная с некоторой точки , осуществляется последовательный переход к некоторым другим точкам до тех пор, пока не выявляется приемлемое решение исходной задачи. При этом градиентные методы могут быть подразделены на две группы.

К первой группе относятся методы, при использовании которых исследуемые точки не выходят за пределы области допустимых решений задачи. Наиболее распространенным из таких методов является метод Франка-Вулфа.

Ко второй группе относятся методы, при использовании которых исследуемые точки могут, как принадлежать, так и не принадлежать области допустимых решений. Однако в результате реализации итерационного процесса находится точка области допустимых решений, определяющая приемлемое решение. Из таких методов наиболее часто используется метод штрафных функций или метод Эрроу-Гурвица.

Остановимся более подробно на методах Франка-Вулфа, штрафных функций и Эрроу-Гурвица.