§1.5. Дискретизация и теорема отчетов (Котельникова)

Для понимания теоремы Шеннона об информационном канале с шумом напомним определения понятий дискретизации и интерполяции.

Определение. Представление непрерывного (аналогового) сигнала x(t) дискретной последовательностью отсчетов x(t_k)=x(k, ∆t), по которым с заданной точностью можно восстановить исходный непрерывный сигнал, называется дискретизацией на равномерной сетке.

Определение. Процесс восстановления дискретизированного сигнала называется интерполяцией. Допустим, у нас есть непрерывное изображение i(x,y). После дискретизации мы получаем дискретное изображение I(x_k,y_m). Затем интерполируем его и переходим к изображению i’(x,y). Естественно возникает вопрос: как нужно проводить дискретизацию, чтобы не происходила потеря информации, т.е. при каких условиях исходное изображение i(x,y) совпадает с восстановленным i’(x,y)? Ответ на этот вопрос может быть получен из теоремы Котельникова.

Теорема. Пусть сигнал s(t) задан на бесконечной оси времени, -∞ < t < ∞, с ограниченной полосой спектра s(ω), тогда справедливо равенство:

(18)

где τ- интервал времени между соседними равноотстоящими отчетами сигнала s(t):

(19)

Т.о., сигнал, описываемый непрерывной функцией времени s(t) с ограниченным спектром, полностью определяется своими значениями, отсчитанными через интервалы времени τ=1/(2F), где F- ширина спектра сигнала. Частота 2F называется частотой Найквиста или частотой дискретизации. Это минимальная частота, с которой нужно посылать импульсы, чтобы не было потери информации. В формуле (19) константу τ обычно называют периодом дискретизации, последовательность s(kτ) – последовательностью дискретизированных значений.

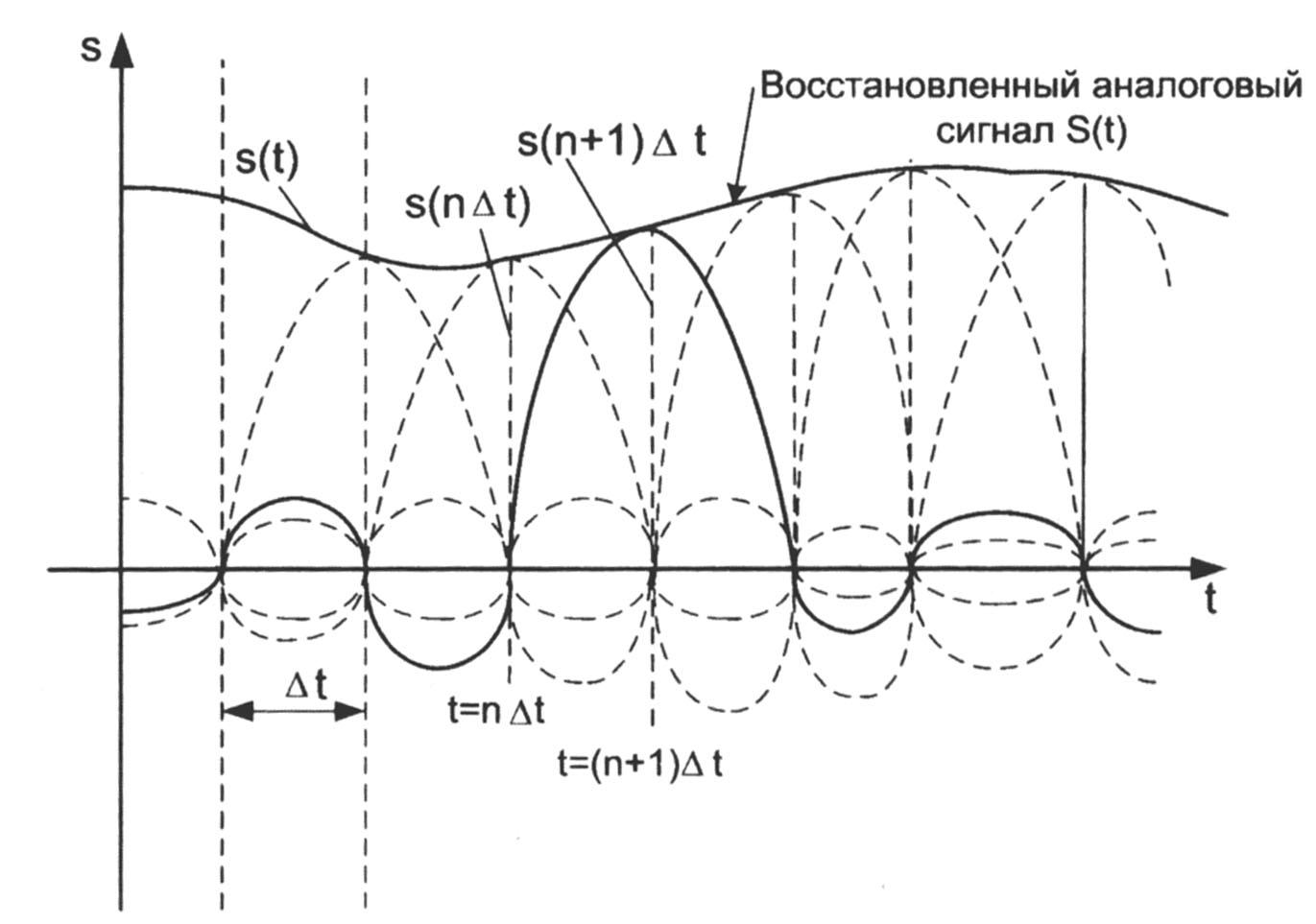
Рис. 45. Представление сигнала s(t) рядом (18)

На рис. 44 проиллюстрировано представление сигнала рядом (18), сплошная линия s(t) представляет сумму сплошного и пунктирных горбов функции в правой части (18), умноженных на величину амплитуд s(k) в точках k.

На практике восстановленная функция, как правило, не совпадает точно c передаваемой функцией s(t). Ошибка обусловлена, например, тем, что спектр передаваемой функции обычно ограничен не резко. Это вытекает хотя бы из того факта, что все реальные сигналы ограничены во времени и, следовательно, имеют неограниченные строго спектры. Выбор интервалов отсчетов τ > 0 означает, что все спектральные составляющие спектра с частотами ω > Ω_max= π τ не передаются и не могут быть восстановлены. Если 2τF > 1, то исходная функция не может быть восстановлена.

Теорема была сформулирована В. А. Котельниковым в 1933 году в его работе «О пропускной способности эфира и проволоки в электросвязи» и является одной из основополагающих теорем в теории и технике цифровой связи.

§1.6. Пропускная способность канала при наличии белого теплового шума

Предположим, что по­меха в системе есть белый тепловой шум, ограниченный полосой частот f. Эта помеха, добавляясь к переданному сигналу, дает принятый сигнал. Белый тепловой шум характеризуется тем, что изменения каждого отсчета независимы от других и что распределение мгновенных значений подчинено гауссовскому закону со стандартным отклонением где P_Ш — средняя мощность помехи. Сколь­ко различных сигналов можно распознать на приемном конце, нес­мотря на наличие обусловленных помехой изменений? Если бы шума не существовало, то число дискретных уровней сигнала было бы бесконечным. В случае наличия шума последний определяет степени различимости отдельных уровней амплитуды сигнала. Если сигнал имеет мощность Р_С, то сигнал, измененный наложенной помехой, будет иметь мощность Р_C + P_Ш. Так как мощность является усредненной характеристикой амплитуды, число различимых уровней сигнала по мощности равно (P_С + P_Ш) / P_Ш, а по амплитуде соответственно:

. (20)

Согласно теореме Котельникова за время Т имеется 2Tf независимых значений, тогда полное число разли­чимых сигналов будет равно:

.

Число битов, которое можно передать за время Т, равно log₂M и скорость передачи и предельная информационная емкость канала согласно (16), определяется как:

. (21)

Формулу (21) вывел К. Шеннон в своей работе «Связь при наличии шума», опубликованной в 1949 г. Из (21) следует, что при фиксированной полосе частот пропускная способность определяется только отношением мощностей сигнала и помех. Ограничение пропускной способности канала связано с тем, что любые используемые для связи сигналы имеют конечную мощность. C = 0 только при P_С + P_Ш = 0. Канал связи обеспечивает передачу информации даже в том случае, если уровень шумов превышают уровень сигнала – это используется для скрытой (неперехватываемой) передачи. Повысить пропускную способность непрерывного канала можно в основном за счет расширения полосы пропускания.

Наибольшую пропускную способность в соответствии с (21) имеют волоконно-оптические линии связи, использующие полосу частот f ~10¹³ Гц.

Рис.46. Зависимость скорости передачи в полосе 1 Гц от соотношения сигнал/шум в канале связи. 1 – граница Шеннона; 2 – использование фазовой модуляции; 3 - использование амплитудной модуляции; 4 - использование частотной модуляции

На рис. 46. приведены данные по эффективность цифровых систем связи при различных типах дискретизации данных. Как видно из графика, на настоящее время еще не достигнут предел, определяемый теоремой Шеннона.

Фундаментальный энергетический предел передачи информации основан на теореме К. Шеннона для максимальной пропускной способности канала связи (21). Для гауссового источника с тепловым шумом можно записать, что P_Ш = kT∙ ΔF, где k = 1,38∙10-23 Дж/K константа Больцмана, T – температура в К°. Тогда (21) можно переписать:

(22)

Вычислим значение средней энергию на один бит информации путем деления средней мощности сигнала на скорость передачи информации из (22):

(23)

вычисляя производную и приравнивая её нулю по

правилу Лопиталя можно получить:

(24)

Таким образом, для передачи по каналу связи с гауссовым шумом одного бита информации необходимо затратить, по крайней мере, энергию, равную kTln2.