§9.Обратные функции.
Примечание:
Основные
понятия об обратной функции
были рассмотрены в главе 4.
Пример 1.
Найти D(f-1) по заданной функции y=f(x), если
у=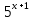
-2.
Решение:
Т.к
функция у=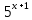
-2
строго возрастает на всей числовой оси,
то существует обратная функция и при
этом:
D(f-1)=E(f)E(f)=(-2;+∞)=D(f-1).
Ответ: (-2;+∞).
Пример 2.
Найти D(f-1) по заданной функции y=f(x), если
у=
+2.
Решение:
Т.к.
функция у=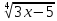
+2
строго возрастает при х5/3,
то существует обратная функция и при
этом:
D(f-1)=E(f)E(f)=[2;+∞)=D(f-1).
Ответ: [2;+∞).
Пример 3.
Найти D(f-1) по заданной функции y=f(x), если
у=5-(х+2)3.
Решение:
Т.к. функция у=5-(х+2)3.строго убывает на всей числовой оси, то существует обратная функция и при этом:
D(f-1)=E(f)E(f)=(-∞;+∞)=D(f-1).
Ответ: (-∞;+∞).
Пример 4.
Найти D(f-1) по заданной функции y=f(x), если
у=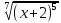
+3.
Решение:
Т.к.
функция у=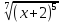
+3 строго
возрастает на всей числовой оси, то
существует обратная функция и при этом:
D(f-1)=E(f)E(f)=(-∞;+∞)=D(f-1).
Ответ: (-∞;+∞).
Пример 5 (самостоятельно).
Найти D(f-1) по заданной функции y=f(x), если
у=4-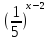
.
Ответ: (-∞;4).
Пример 6(самостоятельно).
Найти D(f-1) по заданной функции y=f(x), если
у=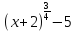
.
Ответ: [-5;+∞).
Пример 7 (самостоятельно).
Найти D(f-1) по заданной функции y=f(x), если
у=3-
.
Ответ:(-∞;+∞)
Пример 8 (самостоятельно).
Найти D(f-1) по заданной функции y=f(x), если
у=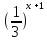
+5.
Ответ: [5;+∞).
Пример 9.
Найти E(f-1)по заданной функции у=f(x), если
у=3-
Решение:
Функция
у=3-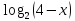
задана в области D(f)=(-∞;4).
Данная функция строго монотонна, а именно, возрастает.
Сделаем контрольную проверку.
Пусть
х1=3
f(3)=3;
x2=2f(2)=2.
x1>x2f(x1)>f(x2)функция возрастает.
Следовательно, существует обратная функция, при этом
E(f-1)=D(f)=(-∞;4).
Ответ: (-∞;4).
Пример 10.
Найти E(f-1)по заданной функции у=f(x), если
у=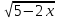
+1.
Решение:
Функция
у=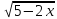
+1
задана в области D(f)=(-∞;2,5]
Данная функция строго монотонна, а именно убывает.
Сделаем контрольную проверку.
Пусть
х1=2
f(2)=1;
x2=-2f(-2)=3.
x1>x2f(x1)f(x2)функция убывает.
Следовательно, существует обратная функция, при этом
E(f-1)=D(f)=(-∞;2,5]
Ответ:(-∞;2,5].
Пример 11.
Найти E(f-1)по заданной функции у=f(x), если
у=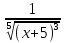
.
Решение:
Функция
у=
задана в области D(f)=(-∞;-5)∪(-5;+∞)
и строго убывает.
Схема графика:
у
х
-5
Следовательно, существует обратная функция, при этом
E(f-1)=D(f)=(-∞;-5)∪(-5;+∞)
Ответ: )=(-∞;-5)∪(-5;+∞)
Пример 12.
Найти E(f-1)по заданной функции у=f(x), если
у=
.
Решение:
Функция
у=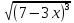
задана в области
D(f)=(-∞;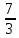
].
Данная функция строго монотонна, а именно убывает.
Сделаем контрольную проверку.
Пусть
х1=2
f(2)=-1;
x2=1f(1)=6.
x1>x2f(x1)f(x2)функция убывает.
Следовательно, существует обратная функция, при этом
E(f-1)=D(f)=(-∞;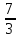
]
Ответ:
(-∞;
]
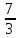Пример 13 (самостоятельно).
Найти E(f-1)по заданной функции у=f(x), если
у=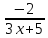
.
Ответ:
(-∞;-
)∪(-
;+∞).
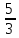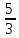Пример 14 (самостоятельно).
Найти E(f-1)по заданной функции у=f(x), если
у=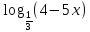
.
Ответ:
(-∞;
).
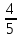Пример 15.
Найти E(f-1)по заданной функции у=f(x), если
у=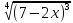
-4.
Ответ: (-∞;5,5].
Пример 16 (самостоятельно).
Найти E(f-1)по заданной функции у=f(x), если
у=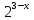
-5.
Ответ: (-∞;+∞).
Пример 17.
Дано:
у=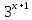
-2.
Найти: 1)обратную функцию;2) построить графики функций f(x)и f-1(x).
Решение:
1.Построим
график функции у=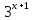
-2
(можно использовать преобразования
графиков: (1) у=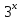
;
(2) у=
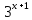-2).
Схема
данного графика:
у
-2
-2
х
1
f-1
f
1
y=x
2.D(f)=(-∞;+∞)
3.E(f)=(-2;+∞);
у=-2горизонтальная
асимптота.
