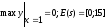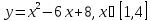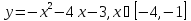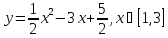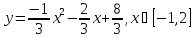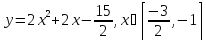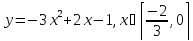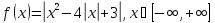- •Оглавление
- •§1 Основные понятия……………………………………………………………………………………………………………………………….2526
- •§2 Решение примеров…………………………………………………………………………………………………………………………….2634
- •§11 Решение примеров………………………………………………………………………………………………………189213
- •Глава 1. Числовые множества.
- •§1 Основные понятия.
- •2; ()2; ()3;…;;…, То с ростом n значения последовательности будут возрастать, но никогда не будут больше числа 3. Такая последовательность имеет предел, который равен иррациональному числу е.
- •§2 Решение задач.
- •Глава 2. Модуль вещественного числа. Решение уравнений и неравенств со знаком модуля.
- •§1 Простейшие уравнения со знаком модуля.
- •Пример 3 Решить уравнения:
- •Решения:
- •§2 Простейшие неравенства со знаком модуля.
- •Пример 1 Решить следующие неравенства:
- •Глава 3. Элементы теории множеств.
- •§1Основные понятия.
- •§2 Решение примеров.
- •Глава 4. Отображение множеств. Виды отображений.
- •§1 Основные понятия и определения.
- •1.Отображение множества а в множество в (общий случай).
- •2.Сюръекция ( отображение множества а на множество в)
- •Решение:
- •§2 Решение примеров.
- •Глава 5.Числовые функции и их свойства.
- •§1 Определение числовой функции. Основные свойства.
- •§2 «Полезные» функции
- •Пример 1 Построить график и провести исследование по предложенной выше схеме.
- •Пример 2
- •§3.Построение графиков и исследование функций со знаком модуля.
- •Глава 6. Построение линий и областей на плоскости, заданных уравнениями и неравенствами.
- •§1.Прямая на плоскости.
- •Уравнение прямой с угловым коэффициентом и начальной ординатой:
- •Уравнение прямой с угловым коэффициентом и проходящей через точку (х0;у0):
- •Уравнение прямой, проходящей через две точки м1(х1;у1) и м2(х2;у2).
- •§2.Уравнение окружности.
- •§3.Построение линий и областей на координатной плоскости.
- •§4. Множества на плоскости.
- •Задача 2.
- •Решение:
- •Задача 3 (самостоятельно)
- •Глава 7. Элементарные функции.
- •§1 Линейная функция.
- •§2 Обратная пропорциональная зависимость.
- •Чётностьнечётность.
- •Промежутки монотонности
- •6.Экстремумов нет, т.К. Функция строго монотонна.
- •1.Новая ось (оу) проходит через точку (-1;0)
- •2.Новая ось (ох) проходит через точку (0;2).
- •Область определения функции:
- •Чётностьнечётность.
- •Чётностьнечётность.
- •§3 Дробнолинейная функция
- •5.Экстремумов нет.
- •4. F(X)≠функция общего вида
- •6.Экстремумов нет.
- •Область определения функции:
- •3): У≠0 корней нет.
- •§4 Степенная функция.
- •На интервале (-∞;0) функция убывает
- •На интервале (-∞;0) функция убывает,
- •§5. Квадратичная функция.
- •Пример 1.
- •Решение:
- •Пример 3.
- •Решение:
- •Найдите значение параметра а. Постройте график функции и найдите минимальное(максимальное) значение функции:
- •Пример 6 (самостоятельно).
- •Пример 7.
- •Решение:
- •§6.Показательная функция.
- •Корней нет, т.К. У≠0.
- •Функция общего вида.
- •Экстремумов нет.
- •Нет корней, т.К. У≠0.
- •Функция чётная .
- •Определить вид отображения (построить график).
- •Определить вид отображения (построить график).
- •Определить вид отображения (построить график).
- •Определить вид отображения (построить график).
- •§7. Логарифмическая функция.
- •Полезные формулы.
- •Докажем это утверждение основываясь на теореме об обратной функции.
- •§8.Сложная функция.
- •1)Если обе функции f и g возрастают,
- •2)Если обе функции f и g убывают,
- •3)Если одна из функций возрастает, а другая убывает,
- •4) Общего вида.
- •Общего вида.
- •4)Чётная функция.
- •§9.Обратные функции.
- •4.Функция непрерывная и строго возрастает
- •5.Находим формулу обратной функции, выражая переменную х через у.
- •Глава 8. Тригонометрические и обратные тригонометрические функции и их свойства.
- •§1.Периодические функции и их свойства.
- •§2.Определение тригонометрических функций.
- •Экстремумов нет.
- •Экстремумов нет.
- •3.Убывает и непрерывна. -1
- •2.Множество значений функции: (-.
- •3.Убывает и непрерывна.
- •2.Множество значений функции:(0;π);
- •4.Функция общего вида.
- •§11.Решение примеров.
- •Пример15 (самостоятельно). Найти периоды данных функций и вычислить значения функций в указанных точках.
- •Пример16. Найти периоды данных функций.
- •Решение:
Пример 6 (самостоятельно).
Найти значение параметра а. Постройте график функции и найдите минимальное (максимальное) значение функции
-
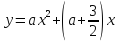 ,
если х=-2 – ось симметрии
,
если х=-2 – ось симметрии -
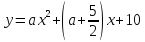 ,
если x=2
- ось симметрии
,
если x=2
- ось симметрии -
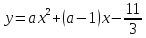 ,
если x=-1/3
- ось симметрии
,
если x=-1/3
- ось симметрии
-
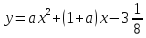 , если x=-1/4
, если x=-1/4
Ответы:
-
a=1/2; min y=-2
-
a=-1/2; max y=8
-
a=3; min у=-4
-
a=-2; max y=-3
Пример 7.
Найти
минимальное (максимальное) значение
функции
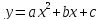 ,
если известно, что её график проходит
через точки:
,
если известно, что её график проходит
через точки:
-
A(0;-3); B(-1;-2); C(2;7);
-
A(-1;-4); B(2;2); C(3;-4);
-
A(2;1); B(1; 4); C(3;4);
-
A(-2,-4); B(-3;-7); C(-4;-16);
Решение:
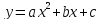
Если график проходит через заданные точки, то координаты точек удовлетворяют уравнению.
-
A(0;-3); B(-1;-2); C(2;7);
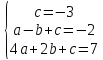 =>
=>
 =>
=>

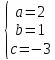


Ответ:

-
A(-1;-4); B(2;2); C(3;-4);
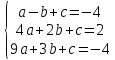 ͞
=>
͞
=>
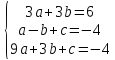 ͞
=>
͞
=>
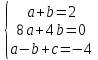 =>
=> 

=>
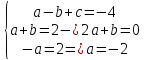 =>
=>
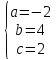 =>
=>

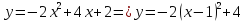
Ответ:
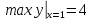
-
A(2;1); B(1;4); C(3;4);

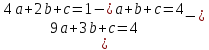 =>
=>
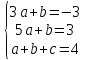 ͞
=>
͞
=>
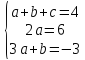 =>
=> 

=>
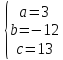 =>
=>
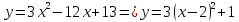
Ответ:
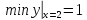
-
A(-2;-4); B(-3;-7); C(-4;-16);
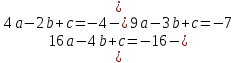 =>
=>
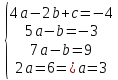 =>
=>
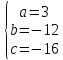



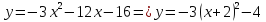
Ответ:
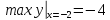
Пример 8.
Найти
минимальное (максимальное) значение
функции
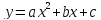 ,
если известно, что её график проходит
через точки:
,
если известно, что её график проходит
через точки:
Координаты точек А,В и С задайте самостоятельно.
Пример 9.
Для
квадратичной функции
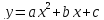 на отрезке [α,β]
найти наибольшее М и наименьшее m
значение функции. Постройте график.
на отрезке [α,β]
найти наибольшее М и наименьшее m
значение функции. Постройте график.
1)
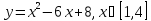
2)
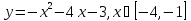
3)
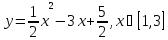
4)
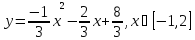
5)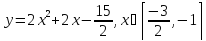
6)
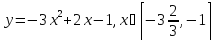
Решение:
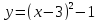 ;
;
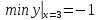
Вычислим значение функции на границах интервала.
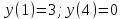
Ответ: M=3; m=-1
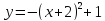 ;
;
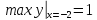
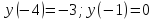
Ответ: M=1; m=-3
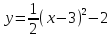 ;
;
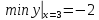
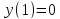
Ответ: M=0; m=-2
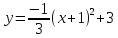 ;
;


Ответ: M=3; m=0
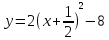 ;
;
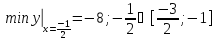
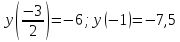
Ответ: M=-6; m=-7,5
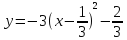 ;
;
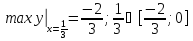
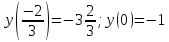
Ответ: M=-1;
m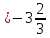
Пример 10.
Задайте
самостоятельно функцию
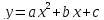 и интервал [α,β].
Найдите наименьшее и наибольшее значение
функции на этом интервале.
и интервал [α,β].
Найдите наименьшее и наибольшее значение
функции на этом интервале.
Пример 11.
Постройте график
функции
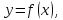 используя основные методы преобразований
графиков. Найдите точки экстремумов и
множество значений функции
используя основные методы преобразований
графиков. Найдите точки экстремумов и
множество значений функции
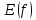
1)

2)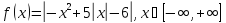
3)

4)
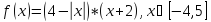
5)
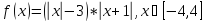
6)
Решение:
Заметим, что
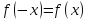 - функция четная, и по условию
- функция четная, и по условию
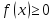
Выполняем последовательно построение графиков следующих функций:
А)
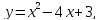 или
или
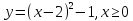
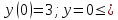
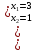
Б)
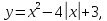 симметричное дополнение
симметричное дополнение
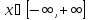 графику (А) относительно оси OY.
графику (А) относительно оси OY.
В)
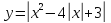 - искомая функция.
- искомая функция.
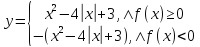 Рис.1
Рис.1
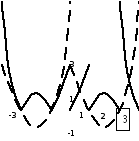
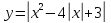
Рис.1
Ответ: Точки экстремумов
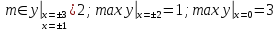
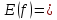
Заметим, что
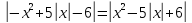
Будем строить
график функции
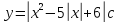 помощью преобразований графиков.
помощью преобразований графиков.
А)
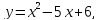
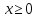

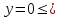
 ;
;
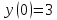
Б)
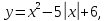
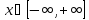
В)
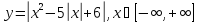
Рис.2
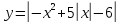
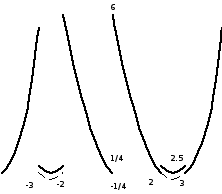
Рис.2
Ответ: Точки экстремумов
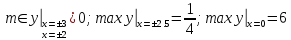
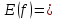
Раскроем знак модуля
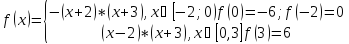
Рис.3
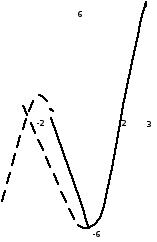
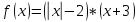
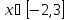
рис. 3
Ответ: Точки экстремумов
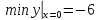
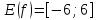
Раскроем знак модуля на данном интервале:
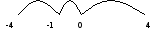
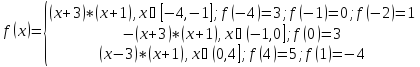
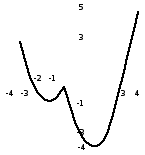
Рис.5
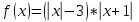
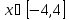
-7
-7
-7
-7
-7
-7
-7
-7
-7
-7
-7
Рис.5
Ответ: Точки экстремумов
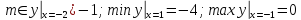
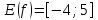
Пример 12.
Построить график функции y = f(x), используя основные методы преобразований графиков. Найдите точки экстремумов и множества значений функции E(f).
1)
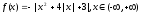
2)
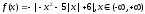
3)
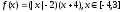
4)
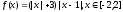
Ответы:
1)
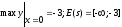
2)
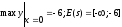
3)
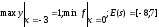
4)