1) Метод степенных рядов.

Решение находится в виде сумм ряда:

(5.5)

Приближенное решение задачи дает частичная сумма этого ряда;

2) метод Эйлера для уравнения с начальным условием .

В процессе решения составляется таблица значений ,

где  отрезок, на котором ищется решение.

Значения y_k+1 определяются по формуле:

. (5.6)

Погрешность вычислений на каждом шаге составляет

, (5.7)

где ;

3) усовершенствованный метод ломаных

Для некоторого повышения точности решения задачи предыдущим методом сначала вычисляют промежуточные значения:

,

а затем находят . (5.8)

4) усовершенствованный метод Эйлера-Коши

Сначала вычисляют «грубое» значение

, (5.9)

которое затем уточняют по формуле

. (5.10)

Погрешность метода на каждом шаге пропорциональна h³;

5) усовершенствованный метод Эйлера с уточнением

Сначала вычисляют , а затем это значение уточняют по формуле:

. (5.11)

Итерации продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения не совпадут. Погрешность метода на каждом этапе имеет порядок h³;

6) метод Рунге-Кутта

На каждом шаге вычисления выполняются по формуле , (5.12)

где ,

.

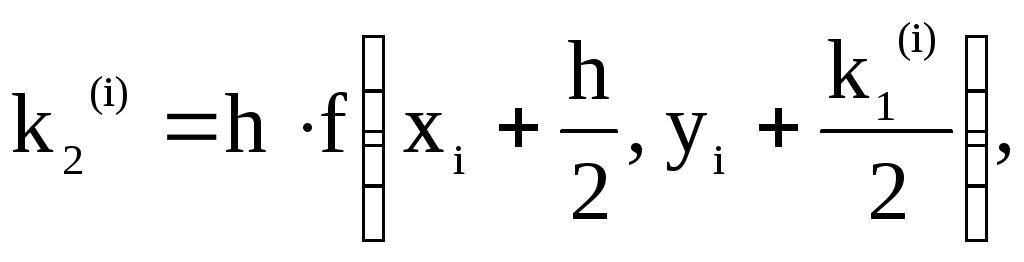
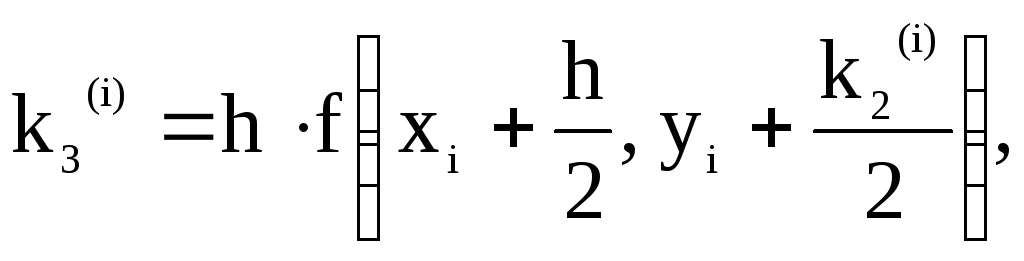
Погрешность метода на каждом шаге имеет порядок ;

7) метод Адамса

7.1) формула с первыми конечными разностями:

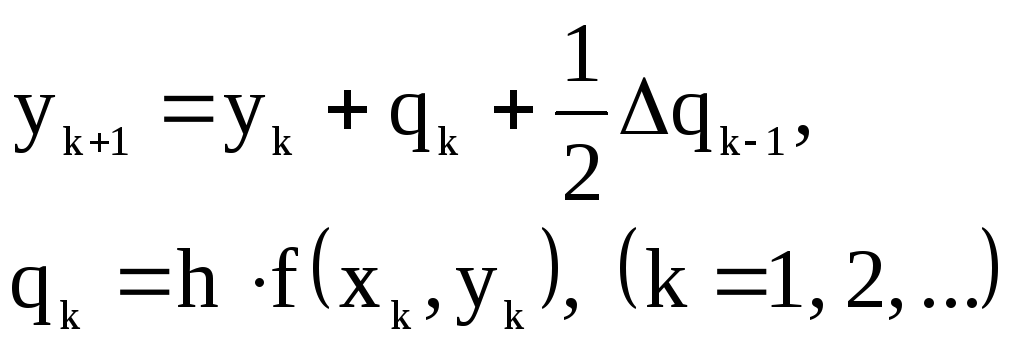(5.13)

 конечная разность 1-го порядка.

Значение y₁ находят любым другим способом, например, применяя метод Эйлера. Погрешность вычислений на каждом шаге имеет порядок h².

7.2) формула со вторыми конечными разностями:

, (5.14)

где  конечная разность 1-го порядка,

 конечная разность 2-го порядка.

Значения y₁ и y₂ находят любыми другими способами. Погрешность на каждом шаге имеет порядок ;

8) метод Милна

Пусть для уравнений кроме начального условия найден и некоторый «начальный отрезок», т.е. значения искомой функции в точках .

Последующие значения функции y_i при i=4, 5, … определяются на каждом шаге следующим образом:

для предсказания используется 1-я формула Милна:

.

Используя , вычисляются и корректируются значения по второй формуле Милна:

. (5.15)

Абсолютная погрешность значения приближенно определяется как .

5.3. Пример решения типовой задачи

Пусть необходимо решить, применяя метод Эйлера, следующее дифференциальное уравнение второго порядка:

y2y+sin(xy)+x=0,

для которого заданы начальные условия: x₀=0, y₀=y(x₀)=1, y₀=y(x₀)=1.

Сначала необходимо понизить порядок дифференциального уравнения. Введём в рассмотрение новую функцию Р(x,y)= y(x,y).

Тогда исходное уравнение может быть представлено системой из двух дифференциальных уравнений 1-го порядка:

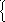y(x,y)=P(x,y)

P(x,y)=2P(x,y)sin(xy)x.

Начальные условия для уравнений этой системы: x₀=0, y₀=1, Р₀=1.

Расчётные формулы для получения решения методом Эйлера имеют вид:

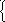y_i+1=y_i+hP_i

P_i+1=P_i+h(2P_isin(x_iy_i) x_i).

Последовательно подставляя в расчётные формулы начальные условия x₀, y₀ и Р₀, а затем и вычисленные на очередном шаге значения x_i, y_i и P_i, можно получить численное решение исходного дифференциального уравнения второго порядка в виде табличного представления функции y(x) c заданным шагом h изменения аргумента х.

Аналогичный приём понижения порядка дифференциальных уравнений может быть применён для произвольного ОДУ n-го порядка (число уравнений в соответствующей системе ОДУ 1-го порядка будет равно n).