Жозеф Луи Лагранж

Законченная система аналитической механики была построена в работах Жозефа Луи Лагранжа, математика и механика, организатора Туринской академии, члена Берлинской Академии наук и, в период с 1766 по 1787 гг., президента физико-математического класса (отделения) этой Академии. В 1788 году вышел его труд «Аналитическая механика», изданный в Париже на французском языке.

В основу динамики Лагранж положил принцип наименьшего действия, который сформулировал следующим образом: «При движении любой системы тел, находящихся под действием взаимных сил притяжения, или сил, направленных к неподвижным центрам и пропорциональных каким-либо функциям расстояний, кривые, описываемые различными телами, а равно их скорости необходимо таковы, что сумма произведений отдельных масс на интеграл скорости, умноженной на элемент кривой, является максимумом или минимумом – при условии, что первые и последние точки каждой кривой рассматриваются как заданные, так что вариации координат, соответствующих этим точкам, равны нулю», то есть

.

Используя принцип наименьшего действия, Лагранж получил для описания движения системы материальных точек общую формулу:

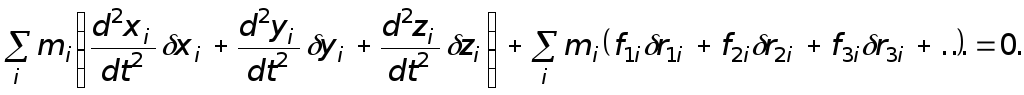
(5.10)

Здесь массы частиц (материальных точек) системы; координаты i-ой частицы; заданные силы, действующие на единицу массы i-ой частицы по направлению к соответствующим центрам; расстояния i-ой частицы до этих центров.

Нетрудно заметить, что это уравнение эквивалентно системе уравнений второго закона Ньютона для системы материальных точек. Из формулы (5.10) Лагранж вывел закон движения центра тяжести системы: «Движение центра тяжести системы свободных тел, расположенных одно по отношению к другому совершенно произвольным образом, всегда таково, как если бы все тела были сосредоточены в одной точке и если бы в то же время каждое из них находилось под действием тех же ускоряющих сил, под влиянием которых оно находится в своем действительном состоянии».

Закон сохранения момента импульса Лагранж записывает в следующем виде

(5.11)

где А, В, С – произвольные постоянные. Эти соотношения представляют собой не что иное, как современный закон сохранения момента импульса:

(5.12)

записанный покомпонентно. В «Аналитической механике» содержался и закон сохранения живых сил, полученный Лагранжем для общего случая системы материальных точек, находящихся под действием центральных сил:

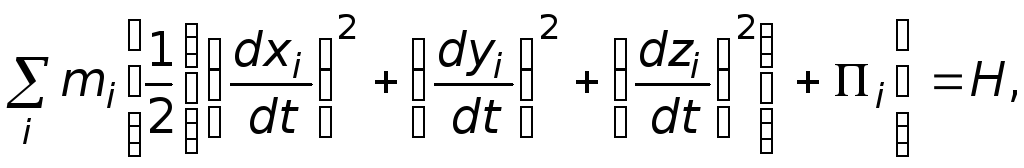(5.13)

где Н обозначает произвольную постоянную, равную значению левой части соотношения в заданный момент времени, а функция, дифференциал которой равен:

где снова означает силу, действующую на единицу массы i-ой частицы по направлению к центру, отвечающему индексу  ; расстояние от i-ой частицы до этого центра. Очевидно, что

где сила, действующая уже не на единицу массы, а на i-ю частицу в целом. При этом

(5.14)

где U – потенциальная энергия частицы в поле некоторого центра. Таким образом, по современным представлениям произведение есть не что иное, как потенциальная энергия i-ой частицы во внешнем поле, а принцип сохранения живых сил представляет собой закон сохранения энергии для консервативных сил.

Особо следует отметить следующий важный шаг, сделанный Лагранжем на пути обобщения методов ньютоновской механики. Он вводит понятие об обобщенных координатах , соответствующих числу степеней свободы системы. Пользуясь принципом наименьшего действия, Лагранж получает уравнения, определяющие закон движения в обобщенных координатах. Эти уравнения в современных обозначениях имеют вид

(5.15)

и носят название уравнений Лагранжа. Здесь T – «живая сила», выраженная как функция обобщенных координат, U – введенная Лагранжем функция, позже получившая название потенциальной энергии. В современной теоретической физике уравнения Лагранжа приобрели огромное значение, далеко выходящее за рамки классической механики.