Глава IV исаак ньютон

Достигнутые опытным естествознанием результаты получили логическое завершение в работах Исаака Ньютона. С 1661 по 1665 г. Ньютон учился в колледже Святой Троицы (Тринити-колледж) Кембриджского университета. Он оказался одним из самых одаренных учеников профессора Исаака Барроу, читавшего лекции по оптике на весьма высоком для того времени уровне. В 1669 году Барроу, решив посвятить себя теологии, передал кафедру своему ученику. Ньютон стал профессором Кембриджа.

Н

Создание дифференциального и интегрального исчислений

аучные интересы Ньютона охватывали практически всю современную ему физику. В своих работах по механике, оптике, астрономии, математике Ньютон сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал независимо от Г. В. Лейбница дифференциальное и интегральное исчисление. Потребность в создании новой математики – математики переменных величин – была огромной. Проблемы квадратуры криволинейных площадей, проведения касательных к кривым, проблемы отыскания максимума и минимума функции успешно решались для отдельных случаев рядом математиков и физиков. Но только Ньютон и Лейбниц смогли разработать общий метод решения таких задач.

Ньютон назвал свой метод «исчислением флюксий», именуя термином «флюксия» то, что мы сегодня подразумеваем под производной. Саму переменную функцию Ньютон назвал «флюентой» (текущей). Для обозначения флюксий он использовал латинские буквы с точками наверху ( и т.д.). Лейбниц же обозначал производные штрихами () или в виде отношения дифференциалов (). Для обозначения квадратуры Лейбниц ввел удлиненную латинскую букву S, т.е. современный знак интеграла. Обозначения, введенные Лейбницем, оказались весьма удобными и сохранились до настоящего времени. Что же касается ньютоновских обозначений, то они употребляются в физике для указания операции дифференцирования по времени. Ньютон специально разъяснял, что в разработанном им методе фигурируют не конечные малые величины Δx, Δy и т.д., а бесконечно малые. В этом разъяснении заключаются современные определения производных и интегралов: и . 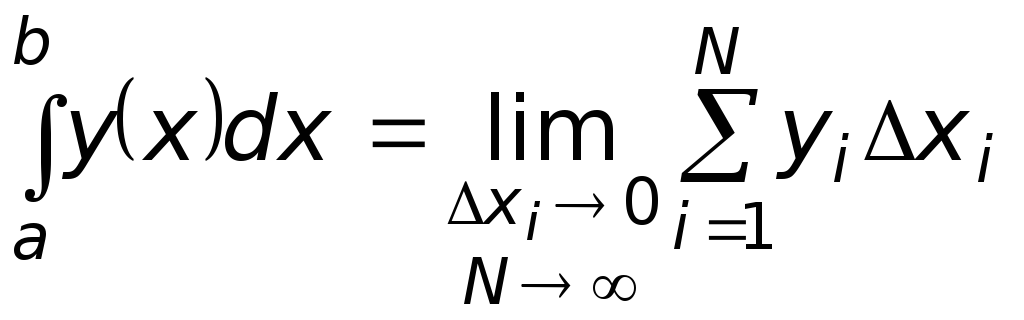Примечательно, что в своих работах по механике Ньютон не пользовался методами дифференцирования или интегрирования, а доказывал свои положения геометрически либо с помощью метода предельных отношений.