Иоханн Кеплер

Большое значение для обоснования гелиоцентрической системы Коперника имели результаты выдающегося немецкого астронома Иоханна Кеплера. Кеплер окончил Тюбингенскую духовную семинарию и был оставлен стипендиатом Тюбингенской академии, впоследствии преобразованной в университет. Перед ним открывалась дорога к богословской карьере. Но сложилось так, что астрономию и математику в Тюбингене преподавал выдающийся педагог Местлин, один из немногих приверженцев учения Коперника. Он разбудил в Кеплере интерес к астрономии, познакомил его с книгой Коперника, и Кеплер сделался горячим сторонником нового учения.

Впоследствии Кеплеру посчастливилось несколько лет работать в Праге под руководством выдающегося астронома Тихо Браге. В 1577 году Браге сумел рассчитать параметры орбиты кометы, пролегавшей вблизи планеты Венера. Результат его расчетов оказался неожиданным для того времени. Опираясь в своих работах на учение Коперника, Браге, в частности, разделял и предположение Коперника о существовании твердой небесной сферы неподвижных звезд, расположенной за орбитой Сатурна. Однако согласно его расчетам получилось, что комета при движении по своей орбите неминуемо должна была столкнуться с ограничивающей Вселенную твердой небесной сферой.

После смерти Браге Кеплеру остались журналы его астрономических наблюдений за 35 лет, и он начал обработку этого гигантского материала. Изучая данные об обращении Марса вокруг Солнца, Кеплер установил, что орбита Марса не является окружностью. Дальнейшие наблюдения и вычисления позволили Кеплеру сформулировать первый закон:

– каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

Эллипсом называется плоская замкнутая кривая, сумма расстояний каждой точки которой от двух точек, называемых фокусами, остается постоянной. Ближайшая к Солнцу точка орбиты называется перигелием, наиболее удаленная – афелием. Степень вытянутости эллипса характеризуется эксцентриситетом , равным отношению расстояния между фокусом и центром эллипса к его большой полуоси. Эксцентриситет окружности равен нулю. Орбиты планет оказались эллипсами, мало отличающимися от окружностей, т.е. с малым значением эксцентриситета, например, у Земли  = 0,017. Кеплеру удалось сформулировать и второй закон (закон площадей):

– радиус-вектор планеты за одинаковые промежутки времени описывает равные площади.

На рис. 1 площади секторов SAB, SCD и SMN равны друг другу. Но длины дуг: CD < AB < MN. Следовательно, линейная скорость движения планеты неодинакова в разных точках орбиты. Скорость планеты оказалась тем больше, чем ближе она к Солнцу. В перигелии скорость планеты максимальна, в афелии – минимальна.

В

Рис. 1. Закон площадей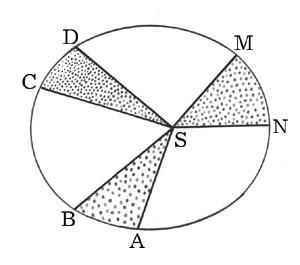

се свои расчеты, критику теорий Птолемея и Тихо Браге Кеплер изложил в книге «Новая астрономия или Небесная физика с комментариями на движение планеты Марс по наблюдениям Тихо Браге», вышедшей в Праге в 1609 году. Через год он узнал об открытии Галилеем четырех спутников Юпитера и изобретении подзорной трубы. По мнению Кеплера, спутники должны были существовать также у Марса (два спутника) и шесть или восемь – у Сатурна. Впоследствии предположения Кеплера во многом подтвердились. В 1619 году вышло очередное его сочинение «Гармония мира», в котором содержался третий закон:

– квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит:

.

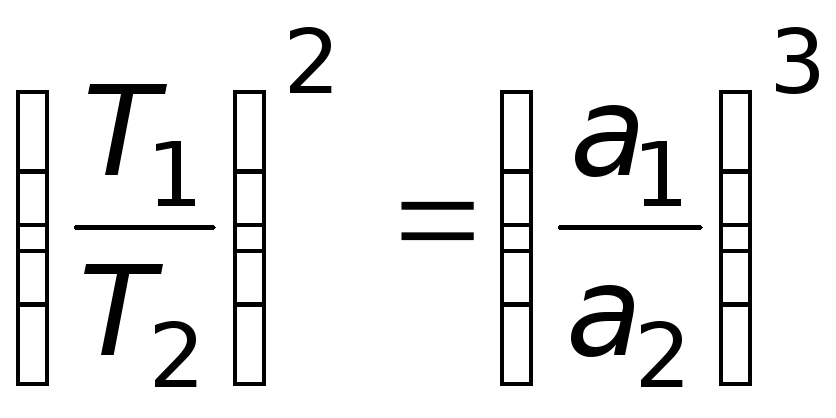Этот закон Кеплера связывал средние расстояния планет от Солнца с их периодами и позволял установить относительные расстояния планет от Солнца, т.к. периоды обращения уже были вычислены.

В целях применения в астрономии Кеплер занимался и вопросами оптики. В 1611 году вышло его сочинение «Диоптрика». Здесь он описывал конструкцию телескопа, рассматривал ход лучей в линзах. Кеплер пришел к выводу о существовании полного внутреннего отражения при переходе света из оптически более плотной в оптически менее плотную среду.

Кеплер разработал теорию солнечных и лунных затмений и способы их прогнозирования, уточнил величину расстояния между Землей и Солнцем, разработал таблицы, позволявшие в любой момент времени с весьма высокой точностью определять положение известных тогда планет. Безусловно, главной заслугой Кеплера было открытие законов движения планет. Но он не сумел объяснить причины этого движения, что не удивительно, так как в то время еще не была разработана динамика, в частности, не существовало понятий взаимодействия и силы. Поэтому открытые Кеплером законы движения планет смогли быть обоснованы лишь после того, как И. Ньютон сформулировал законы динамики и открыл закон всемирного тяготения.