Проверка устойчивости системы

Для проверки устойчивости системы по алгебраическому критерию Гурвица необходимо воспользоваться характеристическим уравнением системы.

Характеристическое уравнение системы имеет вид:

Условия устойчивости сводятся к тому, чтобы все коэффициенты и определители, составленные по схеме, приводимой ниже, были положительными.

Определители образуются из следующей таблицы коэффициентов характеристического уравнения системы:

аn-1	an-3	an-5	.	.	.	.	.	.	0
an	an-2	an-4	.	.	.	.	.	.	0
0	an-1	an-3	.	.	.	.	.	.	0
0	an	an-2	.	.	.	.	.	.	0
0	0	an-1	.	.	.	.	.	.	0
.	.	.	.	.	.	.	.	.	0
.	.	.	.	.	.	.	.	a1	0
0	0	.	.	.	.	.	.	а2	а0

Из этой таблицы для определителя 1,2,…., n-го порядка берутся 1,2,……., n столбцов и строк.

Сама таблица составляется следующим образом. По главной диагонали вписывают последовательно коэффициенты характеристического уравнения, начиная с а_n-1. Столбцы таблиц, начиная с главной диагонали, заполняют вверх по убывающим индексам, вниз – по возрастающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения заменяют нулями.

Например, для системы с характеристическим уравнением

10P⁴ + 3P³ + 5P² + 4P + 1 = 0

таблица коэффициентов будет иметь вид:

3	4	0	0
10	5	1	0
0	3	4	0
0	10	5	1

Определитель первого порядка

Δ₁ = 3,

определитель второго порядка

Δ2 =	3	4
	10	5

определитель третьего порядка

Δ3 =	3	4	0
	10	5	1
	0	3	4

определитель четвертого порядка

Δ4 =	3	4	0	0
	10	5	1	0
	0	3	4	0
	0	10	5	1

Одним из наглядных критериев устойчивости является критерий Михайлова.

Для рассмотрения системы по данному критерию необходимо воспользоваться характеристическим уравнением системы

Заменяя в уравнении на , получим:

Выделяя в уравнении вещественную часть (сумма слагаемых, содержащих в четных степенях), получим четную функцию , равную

Выделяя мнимую часть уравнения (сумма слагаемых, содержащая в нечетных степенях), получим нечетную функцию , равную

Выражение

есть аналитическое представление вектора Михайлова.

Вычисляя значение при изменении частоты от 0 до + и отмечая изменение положения конца вектора на комплексной плоскости, можно судить об устойчивости рассматриваемой системы.

Если кривая, описывающая изменение положения этого вектора (годограф Михайлова), при изменении частоты от 0 до + описывает в положительном направлении (против часовой стрелки) n квадрантов (n - порядок характеристического управления), то система устойчива.

При вращении вектора и при изменении частоты от 0 до + вещественная и мнимая оси будут в устойчивой системе поочередно пересекаться годографом. Каждому пересечению вещественной оси будет соответствовать корень полинома , а каждому пересечению мнимой оси – корень полинома . Таким образом, для оценки устойчивости системы можно воспользоваться нахождением корней полиномов и . Чтобы система была устойчивой, необходимо и достаточно, чтобы корни уравнений и при изменении частоты от 0 до + чередовались и были вещественными.

Пример. Пусть имеется характеристическое уравнение системы

P⁵ + P⁴ + 7P³ + 4P² + 10P + 3 = 0

Подставляя в это уравнение вместо значение , выделим четную функцию частоты и нечетную функцию частоты:

Годограф Михайлова при изменении частоты 0 до + будет иметь вид:

3

Из рисунка видно, что годограф Михайлова описывает в положительном направлении пять квадрантов, значит, система устойчива.

Для оценки устойчивости можно воспользоваться и методом чередования корней. Выделим уравнения четной функции частоты и нечетной функции частоты в следующем виде:

,

.

Определим корни уравнения

,

тогда

,

; .

Определим корни уравнения

Расположим корни и в таблице

	1	2	3	4	5
Корни	0		1,41		2,236
Корни		1		1,73

Корни чередуются, следовательно, система устойчива.

Для проверки устойчивости системы по критерию Найквиста можно воспользоваться уже построенной АФЧХ разомкнутой системы. Как известно, оценка устойчивости производится по относительному положению АФЧХ и точки с координатами (-1; 0). Дополнительных вычислений не требуется.

ПРИЛОЖЕНИЕ

Вывод дифференциальных уравнений элементов систем автоматического регулирования

1. Дифференциальное уравнение двигателя постоянного тока с независимым возбуждением при регулировании частоты вращения изменением напряжения на якоре.

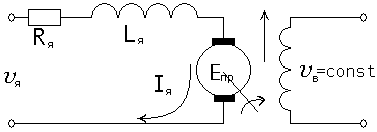
Принципиальная схема

Входная величина - Uя Выходная величина - ω

Исходными физическими уравнениями являются уравнения электрического и механического равновесия.

Схема цепи якоря двигателя позволяет составить уравнение электрического равновесия:

, (1)

где L_я - индуктивность цепи якоря;

R_я - активное сопротивление цепи якоря;

E_пр = 30С_еФ - противоЭДС якоря.

Для двигателей малой и средней мощности индуктивностью якоря можно пренебречь.

Полагая, что вращающий момент двигателя расходуется на преодоление динамического момента, обусловленного моментом инерции вращающихся масс и момента вязкого трения, получим уравнение моментов

, (2)

где С_m- электромеханическая постоянная;

Ф - поток обмотки возбуждения;

J - момент инерции всех вращающихся масс;

 - коэффициент вязкого трения.

Вывод дифференциального уравнения

Выразим из уравнения (2) ток якоря I_я и подставим его в уравнение (1), после преобразования получим уравнение:

, (3)

где - коэффициент внутреннего демпфирования;

- коэффициент пропорциональности между частотой вращения и напряжением.

Окончательно дифференциальное уравнение можно представить в виде

, (4)

где - электромеханическая постоянная времени ;

- передаточный коэффициент двигателя.

Передаточный коэффициент находится по статической характеристике двигателя ω=f(U_я) для заданной рабочей точки.

Передаточная функция элемента

Если к уравнению (4) применим преобразование Лапласа (начальные условия нулевые), то уравнение (4) примет вид

, (5)

Определив отношение лапласова изображения выходной величины к лапласову изображению входной, получим выражение передаточной функции элемента

. (6)

Дополнение

Рассмотрим, как будут выглядеть соответствующие уравнения, если выходной величиной считать угол поворота вала двигателя .

Вывод уравнений (1), (2) остаётся таким же. Учитывая, что ω= и подставив данное выражение для частоты вращения в уравнение (4), получим:

(7)

Передаточная функция для данного случая будет иметь вид:

(8)

2. Дифференциальное уравнение двигателя постоянного тока в случае регулирования частоты вращения путём изменения потока возбуждения при постоянном токе в обмотке якоря.