2.3.2. Графоаналитический метод кинематического анализа рычажных механизмов

Графоаналитический метод определения кинематических параметров механизмов сводится к построению планов их положений, скоростей и ускорений.

План положений механизмов – это графическое изображение взаимного расположения звеньев, соответствующее выбранному расчетному положению начального звена.

План скоростей механизма – это чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент.

План ускорений – это чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизм в данный момент.

Кривошипно-ползунный механизм. На рис. 2.5, а показан план положений механизма для значения обобщенной координаты Для построения плана положений необходимо задаться масштабным коэффициентом , определяемым как

(2.31)

где - действительная длина звена 1; - длина отрезка, изображающего звено 1 на плане положений.

Иногда вместо масштабного коэффициента плана положений задают масштаб плана, который является обратной величиной масштабного коэффициента.

Значение масштабного коэффициента определяет длину отрезка , соответствующего длине звена 2:

План положений позволяет определить угол и координаты точек и :

(2.32)

Для построения плана скоростей должна быть известна кинематическая схема механизма, построенная в масштабе (рис. 2.9, а), и задан закон движения начального звена (например, ).

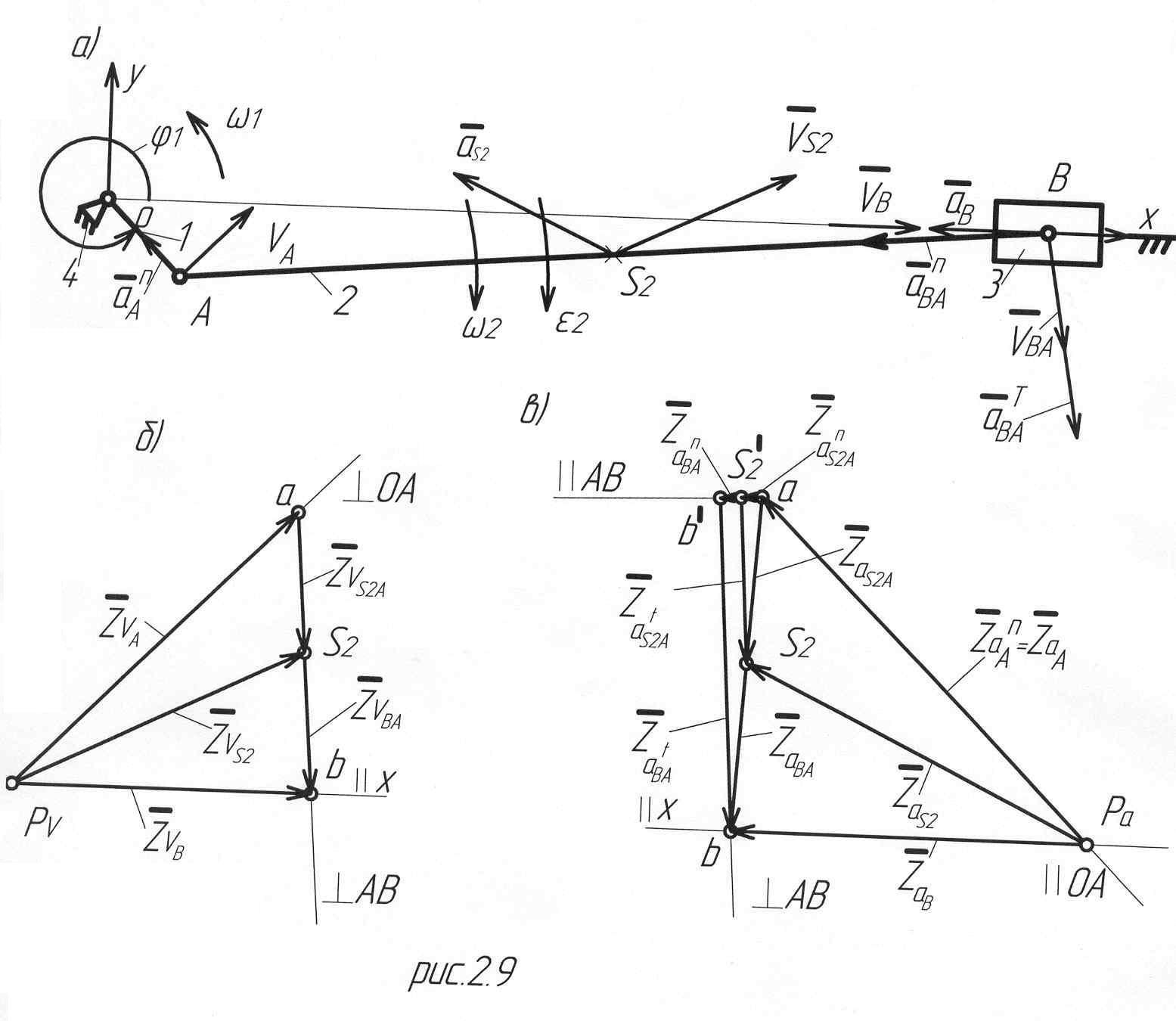
Требуется найти линейные скорости точек , и , и также угловую скорость звена 2.

Построение плана скоростей начинается с определения скорости точки кривошипа

(2.33)

Вектор скорости точки направлен перпендикулярно кривошипу в направлении его вращения.

Скорость точки , принадлежащей звену 2, можно представить как векторную сумму скоростей переносного и относительного движений

(2.34)

Переносным движением звена 2 является поступательное движение его со скоростью точки

а относительным – вращательное движение звена 2 вокруг точки А. Если обозначить относительную скорость через , то

Окончательное векторное уравнение для скорости точки В будет иметь вид

(2.35)

В этом уравнении векторы скоростей, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению – одной чертой.

Для определения указанных неизвестных величин строим план скоростей с выбранным масштабным коэффициентом

(2.36)

Здесь

- длина отрезка, изображающего на плане скорость .

Из произвольной точки полюса плана скоростей (рис. 2.9, б) проведем вектор , перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости . Из конца вектора (точка а) проводим линию в направлении относительной скорости , перпендикулярную , а из полюса - линию в направлении скорости , параллельную . В пересечении указанных линий находим точку b. Вектор изображает скорость точки В, а вектор - скорость . Величины действительных скоростей определяют по формулам

(2.37)

Направление скорости определяется при параллельном переносе вектора в точку В механизма (рис. 2.9, а). Т.к. вектор в точке В механизма направлен в сторону положительной полуоси , знак скорости будет положительным.

Модуль угловой скорости звена 2 будет

(2.38)

Направление находится по вектору . На рис. 2.9, а направлена по часовой стрелке.

Скорость точки определяется с помощью векторного уравнения:

(2.39)

Здесь скорость относительного движения точки находится методом пропорционального деления отрезка ав на плане скоростей, изображающего относительную скорость

(2.40)

Действительная скорость определяется как

(2.41)

Вопросы для самоконтроля.

1. Каковы задачи кинематического анализа рычажных механизмов?

2. Что называется кинематическими параметрами и кинематическими характеристиками звеньев и характерных точек механизмов?

3. Какие известны методы кинематического анализа рычажных механизмов, их достоинства и недостатки?

4. Когда используют метод замкнутых векторных контуров и в чём он заключается?

5. Что представляет собой графоаналитический метод кинематического анализа рычажных механизмов?

6. Что должно быть известно для построения планов скоростей рычажных механизмов?

7. Как определяется масштабный коэффициент плана скоростей?

8. Что называют переносным движением шатуна в кривошипно-ползунном механизме, в котором ведущее звено-кривошип?

9. Что называют относительным движением шатуна в кривошипно-ползунном механизме (ведущее звено-кривошип)?

10. Как определить значение и направление угловых скоростей звеньев механизма?