Лекция № 5

2.4. Силовой анализ рычажных механизмов

Во время движения механизма в его кинематических парах действуют силы, являющиеся силами взаимодействия между звеньями. Эти силы относятся к категории внутренних сил по отношению к механизму в целом. Знание сил в кинематических парах в дальнейшем позволит решить следующие инженерные задачи: расчет звеньев механизма на прочность, жесткость, износоустойчивость и т.п.; расчет подвижных соединений звеньев на долговечность; выбор мощности двигателя и т.д.

Задачей силового анализа рычажных механизмов является определение:

1) сил и пар сил, приложенных к механизму извне;

2) внутренних сил, действующих в кинематических парах;

3) уравновешивающей силы или уравновешивающего момента, которые надо приложить к начальному звену для обеспечения требуемого закона движения выходного звена.

Для силового анализа рычажных механизмов используют метод кинетостатики, условно приложив к каждому подвижному звену механизма главный вектор и главный момент сил инерции. Тогда под действием внешних сил и моментов и инерционных сил весь механизм будет находиться в равновесии.

Следует отметить, что главный вектор и главный момент не имеют никакого физического содержания, т.е. это фиктивные силы, но с их помощью учитывается ускоренное движение звеньев.

Для кинетостатической определимости плоский механизм не должен иметь избыточных связей. Найдём условие кинетостатической определимости плоских рычажных механизмов, которые содержат низшие вращательные и поступательные кинематические пары. Как известно из теоретической механики, сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности.

Во вращательной паре сила, действующая на звено со стороны звена направлена нормально к цилиндрической поверхности соприкосновения обоих звеньев, т.е. проходит через центр шарнира (рис. 2.11, а). Модуль силы и угол неизвестны. Эта пара приносит в расчет две неизвестные величины.

В поступательной паре сила направлена по нормали к поверхности соприкосновения звеньев (рис. 2.11, б). Модуль силы и плечо неизвестны. И эта низшая пара приносит в расчет две неизвестные величины.

Все сказанное о силах относится к силам , приложенным к звену от звена , т.к. силы взаимодействия и связаны третьим законом Ньютона: .

Если плоская кинематическая цепь содержит подвижных звеньев и низших кинематических пар, то для нее суммарное количество неизвестных величин в кинематических парах равно , а количество уравнений равновесия равно , т.к. для каждого звена можно составить 3 уравнения кинетостатики:

Для кинетостатической определимости такой цепи необходимо выполнение условия или . Сопоставив это выражение с выражением (2.1), полученным для плоской структурной группы любого класса с низшими парами, можно сделать вывод, что любая структурная группа, сколь бы сложной она ни была, является статически определимой.

Для плоского механизма без избыточных связей с одними низшими парами формула Чебышева имеет вид или . Оставшиеся уравнений используются для определения уравновешивающих сил или уравновешивающих моментов, приложенных к начальным звеньям. Если и начальное звено совершает поступательное движение, то определяют одну уравновешивающую силу , при вращательном движении начального звена определяют уравновешивающий момент .

На основании вышеизложенного общая методика силового анализа рычажных механизмов без избыточных связей такова: силовой анализ ведется погруппно, начиная от группы, наиболее удаленной от первичного механизма, и заканчивая расчетом самого первичного механизма. Таким образом, силовой расчет проводится в порядке, обратном кинематическому.

При наличии избыточных связей в механизме метод кинетостатики не пригоден, необходимо использовать методы теории упругости.

Существуют два метода силового анализа рычажных механизмов: аналитический и графический. Каждый из них обладает теми же достоинствами и недостатками, указанными в разделе кинематического анализа механизмов.

Независимо от метода расчета исходными данными являются:

1) кинематическая схема;

2) массы и моменты инерции звеньев, положения центров масс звеньев;

3) закон движения механизма;

4) внешнее силовое нагружение.

Внешнее силовое нагружение может быть представлено следующей группой сил и моментов.

1. Массовые внешние силы: силы тяжести ; силы инерции внешние, связанные с движением объекта, на котором находится механизм, , , где - масса - того звена, – ускорение свободного падения, и - горизонтальная и вертикальная перегрузки, равные отношению соответственно горизонтальной или вертикальной составляющей ускорения и величины : Работа этих сил за цикл равна нулю.

2. Массовые внутренние силы – это главный вектор сил инерции и главный момент сил инерции звена где - линейное ускорение центра масс звена, - угловое ускорение звена, - момент инерции - того звена относительно оси, проходящей через центр масс звена перпендикулярно плоскости его движения. Работа этих сил за цикл также равна нулю.

7. Силы полезного сопротивления – это силы, для преодоления которых предназначен механизм. Ими могут быть силы резания, давления, сжатия и другие технологические силовые факторы. Работа за цикл этих сил – отрицательная величина.

8. Силы вредного сопротивления – это внешние и внутренние силы трения. Внешние силы трения возникают в исполнительном устройстве, приводимом в действие механизмом. Внутренние силы трения возникают в кинематических парах. Работа за цикл этих сил также отрицательна.

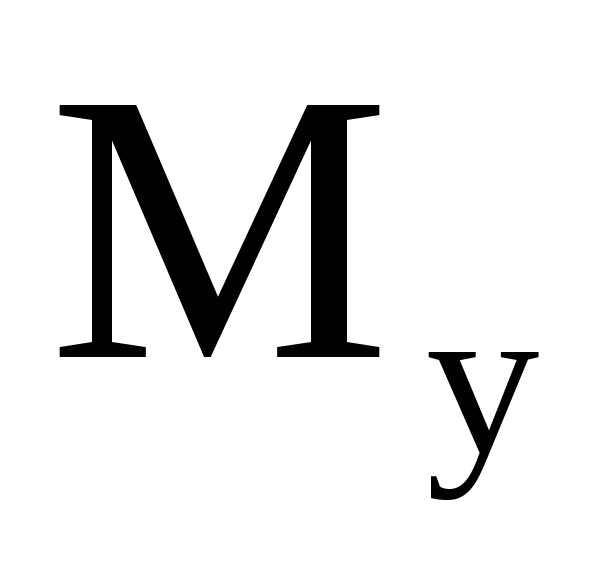9. Движущие силы и моменты – это уравновешивающая сила или уравновешивающий момент , которые должны быть приложены к начальному звену со стороны двигателя. Эти силы за цикл совершают положительную работу.