
Теоретические основы электротехники-2
.pdf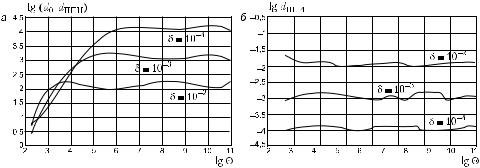
Глава 16. Диагностика электрических цепей |
273 |
аналогично d0. Величина s, входящая в выражение для линейных связей принималась равной трем. Результаты представлены для различных уровней погрешности −, с которыми выполнялись измерения узловых напряжений. Зависимости, представленные на рис. 16.12, à получены для задачи диагностики первого порядка сложности, изображенной на рис. 16.9. Из рис. 16.12, à видно, что применение ППИ при решении задачи диагностики целесообразно уже при Ω > 102, т. е. для большинства практически интересных задач первого порядка сложности. Уже при Ω > 103,5 применение ППИ позволяет более чем в 100 раз уменьшить погрешность решения задачи диагностики.
Íà ðèñ. 16.12, á представлены сглаженные зависимости погрешности решения задачи диагностики цепи второго порядка сложности, изображенной на рис. 16.10, от числа обусловленности матрицы Y, полученные при различных уровнях погрешности измерений −. Расчеты выполнялись с применением принципа повторных измерений. Сопоставляя эти зависимости с аналогичными, но полученными без применения ППИ (рис.16.11, á) можно сделать вывод о высокой эффективности использования этого принципа и для цепей второго порядка сложности. Действительно, погрешность решения задачи диагностики практи- чески не зависит от обусловленности матрицы Y, а среднее значение погрешности близко к максимально достижимому уровню — уровню погрешности измерительных приборов. Как показывают более подробные исследования, минимальное значение Ω, при котором применение ППИ целесообразно для цепей второго порядка сложности меньше, чем для задач диагностики цепей первого порядка сложности. Необходимо отметить, однако, что применение ППИ для диагностики цепей первого порядка сложности требует удвоенного в сравнении с применением стандартного метода узловых сопротивлений объема экспериментальной работы, а при диагностировании цепей второго порядка сложности утроенного объема работы.
Ðèñ. 16.12
На рис. 16.13 представлены в логарифмическом масштабе зависимости отношения d0/dÏÏÈ для решения задачи диагностики первого порядка сложности для цепи переменного тока. Кривые на рис. 16.12, à è ðèñ. 16.13, à, á идентичны. Как показывают численные исследования, для диагностики линейных цепей пере-

274 Часть 2. Теория линейных электрических цепей
менного тока также целесообразно применять ППИ уже при Ω > 1, т. е. практи- чески для всех задач.
Ðèñ. 16.13
Отметим, что в настоящей главе рассматривались в основном резистивные цепи. Однако все результаты справедливы также для диагностики линейных цепей переменного тока при использовании комплексного метода. Особые сечения в таких цепях возникают на частотах, близких к резонансным. Альтернативой применения ППИ в данном случае является выполнение экспериментов на различных частотах. Однако в сложных устройствах выбор частот для проведения диагностических экспериментов затруднен наличием большого числа индуктив- но-емкостных связей. Кроме того свойства математических моделей устройств могут значительно изменяться при изменении частоты, особенно для высокодобротных устройств. Поэтому выполнение опытов на одной частоте предпочтительно.
Глава семнадцатая
Электрические цепи с распределенными параметрами при установившемся режиме
17.1. Электрические цепи с распределенными параметрами
В § 3.3 т. I было указано, что, строго говоря, мы всегда имеем цепи, параметры которых в той или иной мере распределены вдоль участков цепи, и только абстрагируясь от действительности, можно предполагать, что параметры цепи — индуктивность, емкость, сопротивление и проводимость — сосредоточены в определенных участках цепи. Во многих случаях такое допущение не приводит к сколько-нибудь заметным неточностям в результатах проводимого анализа. Изложенная во всех предыдущих главах теория цепей относилась к цепям с сосредоточенными параметрами. Однако мы встречаемся с рядом важных случаев, когда такого рода допущение становится неприемлемым и совершенно необходимо учитывать распределенность параметров вдоль цепи. При этом еще имеем возможность рассматривать электротехническое устройство как электрическую цепь, если оно имеет большую протяженность лишь в одном определенном направлении. В таком случае можно говорить о параметрах, распределенных по длине цепи в этом направлении. Критерием необходимости рассматривать цепь в качестве цепи с распределенными параметрами, как было сказано в § 3.4, т. I, является соотношение между интервалом времени распространения электромагнитных волн вдоль всей длины цепи и интервалом времени, в течение которого токи и напряжения изменяются на величину, составляющую заметную долю от полного их изменения в рассматриваемом процессе. Когда эти интервалы времени сравнимы, то цепь необходимо рассматривать как цепь с распределенными параметрами.
Естественно, что токи и напряжения в таких цепях являются функциями двух независимых переменных — времени t и координаты x, отсчитываемой вдоль указанного выше направления. Соответственно, уравнения, описывающие процессы в этих цепях, являются уравнениями в частных производных. Примерами цепей с распределенными параметрами являются линии передачи электриче- ской энергии, линии связи, высокочастотные коаксиальные линии радиотехни- ческих и телевизионных устройств. Обмотки трансформаторов и электрических машин также должны рассматриваться как цепи с распределенными параметрами при воздействии на них импульсных токов и напряжений, когда промежуток времени изменения токов и напряжений сравним со временем пробега волн вдоль проволоки обмотки.
Параметры цепи могут быть распределены неравномерно вдоль цепи. Однако во многих случаях можно полагать параметры распределенными равномерно вдоль цепи, например для линий передач, в которых сечение проводов, их взаимное расположение и характеристики среды не изменяются по длине линии. Такие линии называют о д н о р о д н ы м и.
В дальнейшем под величинами, обозначаемыми через L, Ñ, r, g è Ì, будем понимать индуктивность, емкость, сопротивление, проводимость и взаимную ин-

276 Часть 2. Теория линейных электрических цепей
дуктивность, приходящиеся на единицу длины линии. Эти параметры, вообще говоря, зависят от частоты. Например, сопротивление r и индуктивность L зависят от частоты вследствие поверхностного эффекта. Исследуя основные процессы в однородных линиях, будем полагать их параметры постоянными. В случае необходимости зависимость параметров от частоты должна быть учтена.
17.2. Уравнения линии с распределенными параметрами
Рассмотрим двухпроводную однородную линию. Величины L è r представляют собой индуктивность и сопротивление пары проводов на единицу длины линии, величины C è g — емкость и проводимость утечки между проводами на единицу длины линии. Координату x будем отсчитывать от некоторой точки линии, в ча- стности от начала линии. Ток в проводах линии зависит не только от t, íî è îò õ, так как на каждом отрезке dx линии ток ответвляется от одного провода к друго-
му в виде тока смещения Cdx ΗΗut и тока проводимости gdxu. Поэтому если ток в проводе в точке x равен i, то в точке x + dx он отличается от i на величину ΗΗxi dx è
равен i + ΗΗxi dx. Согласно принципу непрерывности тока, ток сквозь замкнутую поверхность s (ðèñ. 17.1, à) равен нулю:
|
Ηi |
|
|
Ηu |
|
|
( i) i |
|
dx |
gdxu Cdx |
|
0 |
|
Ηx |
||||||
|
|
|
Ηt |
|
èëè
ΗΗxi gu C ΗΗut .
Ðèñ. 17.1
Точно так же напряжение между проводами зависит не только от t, íî è îò x, так как на каждом отрезке dx линии имеет место падение напряжения в двух проводах линии du1 + du2 (ðèñ. 17.1, á). Это падение напряжения складывается из падения напряжения rdxi в сопротивлении rdx пары проводов и индуктивного
падения напряжения LdxΗΗti, обусловленного индуктивностью Ldx пары проводов, т. е. du1 + du2 rdxi + LdxΗΗti. Сумма падений напряжения в рассматриваемом контуре равна нулю:

Глава 17. Цепи с распределенными параметрами при установившемся режиме |
277 |
|
Ηu |
|
|
Ηi |
0 |
( u) u |
Ηx |
dx |
rdxi Ldx |
|
|
|
|
|
Ηt |
|
èëè
ΗΗux ri L ΗΗti . Таким образом, уравнения линии имеют вид
|
Ηu |
ri L |
Ηi |
; |
|
Ηi |
gu C |
Ηu . |
|
Ηx |
Ηt |
Ηx |
|||||||
|
|
|
|
|
Ηt |
Для однородной линии параметры r, L, g è Ñ не зависят от x. Для неоднородной линии они являются функциями от x.
В общем случае для n-проводной линии, расположенной в воздухе над поверхностью земли, для каждого из проводов необходимо в первом уравнении учитывать также ЭДС взаимоиндукции от токов, протекающих в соседних проводах, а во втором уравнении учитывать также ток смещения между рассматриваемым проводом и всеми соседними проводами. При этом получаем систему из 2n уравнений (так называемых телеграфных уравнений):
|
|
|
Ηuk r i |
L Ηik M |
|
Ηim ; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
m n |
|
|
|
|
|
|
|
|
|
|
|
|
k k |
k |
|
|
|
|
|
km |
|
|
|
|
|
|
|
|
|
Ηx |
Ηt |
|
|
Ηt |
|
|
|
|
|||||
Ηik g u |
g (u |
u ) C |
|
m 1 |
|
|
|
|
|
, |
|||||||
|
Ηuk C Η(uk um ) |
||||||||||||||||
|
|
|
|
m n |
|
|
|
|
|
|
|
m n |
|
|
|
|
|
|
|
k k |
|
|
km k |
m |
k |
|
|
|
km |
|
|
||||
|
Ηx |
|
|
Ηt |
|
Ηt |
|
||||||||||
|
|
|
|
m 1 |
|
|
|
|
|
|
|
m 1 |
|
|
|
|
|
ãäå k 1, 2, ... , ï — номер провода; rk, Lk, gk, Ck — собственные параметры k-го провода на единицу длины с учетом влияния земли; Mkm è Ckm — взаимная индуктивность и емкость между k-ì è m-м проводами на единицу длины линии с уче- том влияния земли.
Рассмотрение частного случая — двухпроводной линии, которое будет выполнено в последующих параграфах, представляет интерес не только потому, что это наиболее простой случай, позволяющий наиболее наглядно показать основные особенности процессов в цепях с распределенными параметрами, но также и потому, что во многих случаях трехфазная линия может быть заменена эквивалентной ей однофазной двухпроводной линией. Это можно сделать при синусоидальном процессе, если все провода находятся в одинаковых условиях, т. е. если осуществлена так называемая транспозиция проводов — последовательная перестановка их местами, и если полный цикл транспозиции значительно меньше длины волны тока и напряжения в линии (см. § 17.5). При этом для симметричных трехфазных напряжений прямой и обратной последовательности токи в проводах также образуют симметричные системы соответственно прямой и обратной последовательности. В этом случае достаточно рассматривать процесс в одной фазе, заменяя трехфазную линию эквивалентной ей однофазной двухпроводной линией. Для напряжений и токов нулевой последовательности трехпроводную трехфазную линию также можно заменить эквивалентной двухпроводной, причем обратным проводом в этом случае является провод, эквивалентный земле при трехфазной линии.

278 Часть 2. Теория линейных электрических цепей
17.3. Решение уравнений однородной линии при установившемся синусоидальном режиме
При установившихся режимах токи и напряжения изменяются во времени по периодическому закону. Представив периодические функции времени в виде ряда Фурье, можно произвести расчет отдельно для каждой синусоидальной составляющей этого ряда и вследствие линейности цепи получить результирующий процесс, пользуясь методом наложения. Поэтому достаточно произвести анализ процессов в линии при синусоидальных токах и напряжениях.
Пусть ток и напряжение в линии изменяются во времени по синусоидальному закону с угловой частотой . Пользуясь комплексным методом, напишем уравнения линии для комплексных действующих напряжения U è òîêà I:
dUdx rI j LI; dxdI
КомплексныеU è I являются функциями только x, и, соответственно, уравнения в частных производных для мгновенных u è i перешли в обыкновенные дифференциальные уравнения для U è I.
Дифференцируя первое уравнение по x и используя второе, находим
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
d U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
(r j L)(g j C)U |
Ξ U |
, |
|
||||||||||||||||
|
|
|
dx 2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ãäå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ξ |
|
|
|
|
|
|
|
|
|
|
|
jΠ. |
|
||||||||||
|
|
|
(r j L)(g j C) |
|
||||||||||||||||||||||
Решение уравнения для U имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
U A e Ξx |
A |
eΞx . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Из первого уравнения линии находим комплексный ток: |
||||||||||||||||||||||||||
I |
|
1 |
|
|
|
dU |
|
|
|
|
Ξ |
|
(A e Ξx |
A |
eΞx ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
r j L dx |
|
r j L |
1 |
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
g j C |
|
(A e Ξx A |
eΞx ) |
1 |
(A e Ξx A |
eΞx ), |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
r j L |
1 |
|
2 |
|
|
|
Z |
1 |
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ãäå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Z |
|
|
r j L |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g j C |
|
|
|
|
||||||||
Комплексные величины Ξ + jΠ è Z являются основными характеристиками однородной линии и носят наименования: Ξ — ê î ý ô ô è ö è å í ò ð à ñ ï ð î - ñ ò ð à í å í è ÿ ë è í è è, Z — в о л н о в о е, или х а р а к т е р и с т и ч е с к о е, сопротивление линии, — к о э ф ф и ц и е н т з а т у х а н и я, Π — ê î ý ô ô è ö è å í ò ô à ç û.
Смысл всех этих наименований будет ясен из рассмотрения бегущих волн в линии (см. § 17.5). Обратим внимание на то, что > 0 и Π > 0. Действительно,


280 Часть 2. Теория линейных электрических цепей
Как и всякий четырехполюсник, линия может быть заменена Т- или П-образ- ной, в данном случае симметричной, эквивалентной схемой. Параметры эквивалентных схем вычисляются через постоянные A, B, C è D по формулам, приведенным в § 13.2.
17.4. О моделировании однородной линии цепной схемой
Рассмотрение линии с распределенными параметрами как четырехполюсника и, соответственно, замена линии эквивалентной Т- или П-образной схемой возможны только в том случае, если интересуемся напряжениями и токами только
âначале и в конце линии. Если же желаем изучать распределение напряжения и
тока вдоль линии, то необходимо ее рассматривать как цепь с распределенными параметрами и пользоваться приведенными ранее уравнениями, в которыхU è I являются функциями x. Однородную линию можно рассматривать как однородную цепную схему с бесконечно большим числом элементарных звеньев. Поэтому приближенно можно линию конечной длины заменить цепной схемой с конечным числом звеньев, обладающих конечными значениями параметров. Такая замена будет давать тем более точные результаты, чем большее число звеньев будет содержать цепная схема.
Эти соображения имеют весьма большое значение для моделирования линий. Для экспериментального изучения в лабораторных условиях процессов в длинных линиях, а также процессов в различных системах, соединенных длинными линиями, обычно линии заменяют эквивалентными им цепными схемами. Точ- ность моделирования будет тем больше, чем большее число звеньев будет содержать цепная схема.
Одного звена, заменяющего линию, достаточно, если интересуемся соотношениями между напряжениями и токами только в начале и в конце линии и только при одной частоте установившегося синусоидального режима. Если же желаем знать связь между напряжениями и токами хотя бы только в начале и
âконце линии, но при разных частотах, например для разных гармоник несинусоидальных токов и напряжений, то моделировать всю линию одним Т- или П-образным звеном уже недостаточно. Это следует из того, что параметры такого звена, как видно из вышеприведенных формул, сложным образом зависят от
характеристик линии Z è Ξ, которые в общем случае, в свою очередь, сложным образом зависят от частоты.
Моделировать линию цепной схемой с достаточным числом звеньев и подавно необходимо при изучении распределения напряжения и тока вдоль линии.
Выбор числа звеньев в модели линии зависит от тех задач, которые ставятся при исследовании. Большей частью бывает достаточно взять 10–20 звеньев.
17.5. Бегущие волны
Рассмотрим выражение, полученное в § 17.3 дляU, причем введем обозначения
U ! 21(U1 I1Z)e Ξx U !1e Ξx U !1ejΨe Ξx ;

Глава 17. Цепи с распределенными параметрами при установившемся режиме |
281 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Ξx |
|
|
|
|
Ξx |
|
|
j? |
|
Ξx |
|
|
|
|
||||
|
|
|
U |
|
|
|
|
|
(U |
1 |
I |
Z)e |
|
U e |
|
U e |
|
e |
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
. |
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда при Ξ + jΠ имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
e |
Ξx |
|
|
Ξx |
U |
|
e |
x |
e |
j Ψ Πx |
U e |
x |
e |
j ? Πx |
||||||||
U |
U |
! |
U |
U |
!1 |
|
|
U e |
|
|
!1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
и, переходя от комплексного напряженияU к изображаемому им напряжению u, получим
u u |
|
u |
|
|
U |
|
e x sin t Ψ Πx |
|
U |
e x sin t ? Πx . |
! |
2 |
!1 |
2 |
|||||||
|
|
|
|
|
|
|
|
. |
Таким образом, u ìîжно рассматривать как сумму двух составляющих u! è u . Из выражения u! 
 2U !1e x sin( t Ψ Πx) следует, что при x const, ò. å. â äàí-
2U !1e x sin( t Ψ Πx) следует, что при x const, ò. å. â äàí-
ной точке линии, напряжение u! является синусоидальной функцией времени. Пусть 0 и e– x l. Тогда, положив t const, нетрудно убедиться, что при 0 напряжение u! в данный момент времени будет распределено вдоль линии также по синусоидальному закону. При этом длина Χ синусоидальной волны, изображающей этот закон распределения напряжения u!, т. е. расстояние между ближайшими точками, в которых фазы напряжения u! различаются на 2#, равна 2#/Π. Это синусоидальное распределение напряжения, или, как говорят, волна напряжения, перемещается вдоль линии от начала к ее концу с постоянной скоростью, равной v /Π. Действительно, sin ( t + Ψ – Πx) ïðè x x0 + t/Π будет вели- чиной постоянной, и, следовательно, напряжение, существовавшее в некоторый момент времени в произвольно выбранной точке x, будет оставаться неизменным, если эта точка начнет перемещаться вдоль линии со скоростью v /Π. Так как при этой скорости остается неизменной фаза колебания, то ее называют ф а - з о в о й с к о р о с т ь ю в о л н ы. Такого рода волны, перемещающиеся вдоль некоторого направления, называют б е г у щ и м и в о л н а м и. При > 0 наличие множителя e– x показывает, что амплитуда волны по мере продвижения последней вдоль линии затухает по показательному закону и что распределение напряжения вдоль линии в любой момент времени может быть изображено синусоидой, затухающей по тому же закону (рис. 17.2). Поэтому коэффициент называют коэффициентом затухания. Так как фаза напряжения изменяется с изменением x, то коэффициент Π, характеризующий это изменение фазы, называют коэффициентом фазы.
При помощи аналогичных рассуждений можнî показать, что вторая составляющая u 
 2 U .e x sin ( t + ? + Πx) представляет собой волну такой же длины Χ 2#/Π, êàê è u!, бегущую вдоль линии со скоростью v – /Π, т. е. от конца линии к ее началу. Амплитуда этой волны, как показывает наличие множителя e x, возрастает по показательному закону от начала линии к ее концу, или,
2 U .e x sin ( t + ? + Πx) представляет собой волну такой же длины Χ 2#/Π, êàê è u!, бегущую вдоль линии со скоростью v – /Π, т. е. от конца линии к ее началу. Амплитуда этой волны, как показывает наличие множителя e x, возрастает по показательному закону от начала линии к ее концу, или,
иными словами, затухает по показательному закону по мере продвижения волны от конца линии к ее началу. Волны, бегущие от начала линии к ее концу,

282 Часть 2. Теория линейных электрических цепей
будем называть п р я м ы м и в о л н а м и, а волны, бегущие в обратном направлении, — о б р а т н ы м и в о л н а м и.
Аналогично, рассматривая выражение для тока I, можем написать I I ! I , |
||||||||||||
|
|
1 |
|
|
Ξx |
|
|
1 |
|
|
Ξx |
|
ãäå I ! |
|
|
(U1 |
I1Z)e |
|
; I |
|
|
(U1 |
I1Z)e |
|
. Соответственно, для мгновен- |
2Z |
|
2Z |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
ных значений получаем i i! + i |
, причем i! — прямая волна тока, а i — обратная |
|||||||||||
волна тока. |
|
|
|
|
|
|
|
|
|
|
||
Легко видеть, что отношение напряженияU ! прямой волны к току I ! прямой волны равно волновому сопротивлению линии Z, а для обратных волн соответ-
ствующее отношение равно (–Z): |
|
|
|
||
|
U ! |
Z; |
U |
Z. |
(*) |
|
|
||||
|
I ! |
I |
|
|
|
Появление обратных волн можно рассматривать как результат отражения прямых волн от конца линии. Соответственно, прямые волны называют также п а д а ю щ и м и, а обратные — о т р а ж е н н ы м и. К о э ф ф и ц и е н т о м о т р а -
æ å í è ÿ í à ï ð ÿ æ å í è ÿ qu от конца линии называют отношение отражен- |
||||||||||||||||||||
ной волны U |
к прямой волне U ! |
|
напряжения в конце линии. Соответственно |
|||||||||||||||||
ê î ý ô ô è ö è 2å í ò î ì î ò ð à æ å í |
2è ÿ |
ò î ê à qi |
называют отношение I |
2 |
ê I !2 . |
|||||||||||||||
Найдем выражение для qu è qi через волновое сопротивление Z линии и сопро- |
||||||||||||||||||||
тивление Zïð приемника, на которое замкнута линия на ее конце. |
|
|
||||||||||||||||||
Имеем на конце линии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U 2 U ! U |
|
|
|
I 2 |
I ! |
I |
|
U |
! |
|
U |
|
|
||||||
|
|
; |
|
|
2 |
2 |
. |
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
Z |
|
Z |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2U |
2 U 2 I 2 Z I 2 (Z ïð Z); 2U ! 2 U 2 I 2 Z I 2 (Z ïð Z); |
|
|
|||||||||||||||||
следовательно, |
|
|
|
U |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Z |
ïð |
|
|
|
|
|
|
|
|||||
|
q |
|
|
|
2 |
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
U |
|
|
|
Z |
|
Z |
|
|
|
|
|
|
|
|||
|
|
|
|
|
! 2 |
|
ïð |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разделив первое равенство (*) на второе, получаем qi/qu –1, ò. å.
q |
q |
Z Z ïð |
. |
|
|||
i |
u |
Z Z ïð |
|
|
|
||
Если линия замкнута на конце на сопротивление, равное волновому, Zïð Z, òî qu 0 è qi 0, т. е. в линии будут отсутствовать отраженные (обратные) волны. При этом в любой точке линии отношение напряжения к току равно волновому
сопротивлению:
U U ! Z. I I !
Если линия на конце разомкнута, т. е. имеем так называемый режим холостого хода, то Zïð , qu 1 è qi –1. Следовательно, на конце линии падающая U !2
