Файловый архив студентов. Файловый архив студентов.
1260 вузов, 4603 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Сочинский Государственный Университет
Предмет:
Электрооборудование подстанций промышленных предприятий
Файл:

Теоретические основы электротехники-2

.pdf
Скачиваний:
93
Добавлен:
05.04.2018
Размер:
5.97 Mб
Скачать
☆
Ðèñ. 13.4

Глава 13. Анализ общих свойств четырехполюсников

173

В некоторых случаях оказывается целесообразным в качестве заданных и искомых величин четырехполюсника выбирать совокупности I1, U 2 è I 2 , U1. При таком выборе уравнения четырехполюсника удобно представить через его Í-па- раметры, называемые гибридными. Связь между величинами I1,U 2 è I 2 ,U1 можно записать в виде

U

H

11

I

H U

,

I

H

21

I

H U

.

1

 

1

12

2

 

2

 

1

22

2

 

Параметр Í11 имеет размерность сопротивления, Í22 — проводимости, параметры Í12, Í21 — безразмерные.

Решая эти уравнения относительно соответствующих токов и напряжений, можем выразить Í-параметры через A, Z, Y-параметры четырехполюсника. Между Í-параметрами существует связь, выражаемая соотношеним Í21 Í12.

Если поменять местами входные и выходные зажимы четырехполюсника (см. рис. 13.2), то полу- чим схему, изображенную на рис. 13.3. Из сопоставления рис. 13.2 и 13.3 видим, что это соответствует

замене U1 íà U 2 , U 2 íà U1, I1 íà –I 2 è I 2 íà –I1. Ïðî- Ðèñ. 13.3 изведя такую замену в уравнениях четырехполюс-

íèêà

U

AU

2

BI

;

I

CU

2

DI

,

1

 

2

 

1

 

2

 

соответствующих схеме рис. 13.2, и учитывая, что AD – BC 1, получим уравнения четырехполюсника рис. 13.3 в виде

U

DU

2

BI

;

I

CU

2

AI

.

1

 

2

 

1

 

2

 

Таким образом, если поменять местами вход и выход четырехполюсника, то в уравнениях меняются местами параметры A è D.

Симметричным называют четырехполюсник, свойства которого одинаковы со стороны обеих пар зажимов. Очевидно, при этом A D.

Выше были получены соотношения Y12 –Y21 è Z12 –Z21 для уравнений че- тырехполюсника в системах Y-параметров и Z-параметров. Изменение порядка индексов у величин Y12 è Z12 приводит к изменению знака величины вследствие того, что положительное направление потока энергии принято на входных зажимах к четырехполюснику, а на выходных — от четырехполюсника (см. рис. 13.2).

Ñучетом этого принцип взаимности не нарушается. Если положительное направление тока, а соответствен-

но, и потока энергии на выходных зажимах изменить на противоположное, т. е. принять положительное направление энергии на входных и выходных зажимах одинаковым по отношению к четырехполюснику (рис. 13.4), то следует изменить знак тока I 2 во всех уравнениях. Что-

бы уравнения четырехполюсника остались неизменными, т. е. сохранился знак «плюс» перед всеми его членами, необходимо изменить знаки следующих ко-

эффициентов: Y21, Y22, Z12, Z22, Â, è D, H21, H22. При этом будем иметь Y12 Y21;

Z12 Z21 è AD – BC –1, Í12 –Í21.

174 Часть 2. Теория линейных электрических цепей

Выбор положительных направлений согласно рис. 13.2 целесообразен, как было отмечено, при рассмотрении четырехполюсника как устройства для передачи энергии или сигнала от первичных (входных) ко вторичным (выходным) зажимам. Выбор положительных направлений согласно рис. 13.4 целесообразен, когда четырехполюсник рассматривается просто как часть сложной электриче- ской цепи.

13.2. Эквивалентные схемы четырехполюсника

Так как пассивный четырехполюсник характеризуется только тремя независимыми параметрами, то простейшая эквивалентная схема четырехполюсника должна содержать три элемента. На рис. 13.5 изображена так называемая Т-о б -

 

ð à ç í à ÿ ý ê â è â à ë å í ò í à ÿ

с х е м а четырехполюс-

 

íèêà, íà ðèñ. 13.6 — Ï-î á ð à ç í à ÿ ý ê â è â à ë å í ò í à ÿ

 

ñ õ å ì à.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВыразимU

1 è I1 черезU

2

 

è I 2 для Т-образной эквива-

Ðèñ. 13.5

лентной схемы н сопоставим эти выражения с уравне-

ниями

четырехполюсника,

записанными в

 

системе

 

 

 

A-параметров:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

Z

I

 

Z

2

I

U

; I

I

 

(Z

2

I

U

2

)Y

0

 

 

 

1

1

1

 

 

2

 

 

2

 

 

 

 

1

 

2

 

 

 

 

 

2

 

 

 

 

 

и, следовательно,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

(1 Z Y

0

)U

 

(Z

1

Z

2

Z

Z Y

0

)I

AU

2

BI

;

 

1

 

1

2

 

 

 

 

 

 

 

1

 

2

 

 

 

2

 

 

 

 

2

 

Ðèñ. 13.6

 

 

I Y

U

(1 Z Y

0

)I

CU

 

DI

.

 

 

 

 

 

 

 

1

 

0

2

 

 

 

 

2

 

2

 

 

 

 

2

 

 

 

2

 

 

 

 

 

Отсюда получаем связь между параметрами четырехполюсника и его эквивалентной Т-образной схемы:

A 1 Z1Y0 ; B Z1 Z 2 Z1Z 2Y0 ; C Y0 ; D 1 Z 2Y0

è

 

 

 

 

 

 

 

 

 

 

 

 

 

A 1

 

 

 

 

 

D 1

 

 

 

 

 

 

 

 

 

Y

 

C;

 

Z

 

 

;

Z

 

 

.

 

 

 

 

 

 

 

 

0

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Аналогично для П-образной эквивалентной схемы

 

 

 

 

 

U

 

Z

0

(I

Y U

2

) U

; I

Y U

Y U

2

 

I

 

 

1

 

 

 

 

2

 

2

 

 

 

 

2

 

1

 

 

1

1

 

2

 

2

 

и, следовательно,

 

U

(1 Y

 

 

)U

Z

 

I

AU

BI

 

 

 

 

 

 

Z

0

0

;

 

 

 

 

 

1

 

 

 

 

 

2

 

 

 

2

 

 

2

 

 

 

2

 

2

 

 

 

 

I

(Y

Y

2

Y Y

Z

0

)U

2

(1 Y Z

0

)I

2

CU

2

DI

.

1

 

1

 

 

 

 

1

2

 

 

 

 

 

 

 

1

 

 

 

 

 

 

2

 

Отсюда получаем связь между параметрами четырехполюсника и его П-образ- ной эквивалентной схемы:

A 1 Y2 Z 0 ; B Z 0 ; C Y1 Y2 Y1Y2 Z 0 ; D 1 Y1Z 0

è

 

 

 

D 1

 

 

 

 

A 1

 

Z

 

B; Y

 

;

Y

 

 

.

 

0

1

B

 

 

2

 

B

 

 

 

 

 

 

 

 

Для симметричного четырехполюсника À D, и, соответственно, в эквивалентных схемах Z1 Z2 è Y1 Y2.

Глава 13. Анализ общих свойств четырехполюсников

175

13.3. Экспериментальное определение параметров четырехполюсника

Для экспериментального определения параметров четырехполюсников нет необходимости производить измерения при номинальных напряжениях и токах. Достаточно выполнить измерения при холостом ходе, когда Zïð è I 2 0,

и при коротком замыкании на вторичных зажимах, когда Zïð 0 è U 2 0. Такая

возможность имеет особо большое значение для измерения параметров мощных устройств, так как мощность в опытах холостого хода и короткого замыкания значительно меньше мощности в номинальном режиме. При холостом ходе и коротком замыкании подводимая к первичным зажимам мощность идет только на покрытие потерь внутри четырехполюсника. При номинальном режиме она зна- чительно больше, так как происходит передача энергии во вторичную цепь к приемнику.

Будем отмечать величины в первичной цепи дополнительными индексами: при холостом ходе — индексом 0, при коротком замыкании — индексом «к». Пусть во вторичной цепи при холостом ходе напряжениеU 2 , а при коротком замыкании ток I 2 будут номинальными. Имеем

 

 

 

;

 

 

0

 

U

10

AU 2

I10

CU 2

;2

(*)

 

 

 

 

 

 

1

;

 

2

 

U

1ê

BI 2

 

I1ê

DI 2

.3

 

Налагая эти режимы друг на друга, получаем

U10 U1ê AU 2 BI 2 U1;

I10 I1ê CU 2 DI 2 I1.

Отсюда видно, что для определения значений U1, I1, которые будут иметь место при номинальном режиме, достаточно произвести опыты холостого хода и короткого замыкания при номинальных U 2 è I 2 .

Для линейных четырехполюсников установление номинальных U 2 è I 2 не обязательно, так как может быть выполнен пропорциональный пересчет.

Из выражений (*) имеем

Z

 

 

U1ê

 

B

;

Y

 

I10

 

C

.

1ê

 

 

 

 

 

 

I1ê

 

D

10

U10

 

A

 

 

 

 

 

 

 

Для симметричного четырехполюсника измерения сопротивления короткого замыкания Z1ê и проводимости холостого хода Y10 со стороны первичных зажимов достаточно, так как существуют связи AD – BC 1 è A D.

Для несимметричного четырехполюсника, когда A D, необходимо еще выполнить дополнительный опыт, произведя измерение со стороны вторичных зажимов либо при холостом ходе, т. е. при разомкнутых первичных зажимах либо при коротком замыкании первичных зажимов. Так как перестановка местами входа и выхода приводит к перестановке местами параметров A è D, то получим

Z 2ê B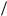A; Y20 C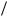D .

176 Часть 2. Теория линейных электрических цепей

Из уравнений четырехполюсника, записанных для Z-параметров или Y-пара- метров, видно, что имеют место следующие соотношения:

Z

 

 

1

 

Z

 

;

Z

 

 

1

 

Z

 

 

;

Z

 

 

 

Z

 

 

Z12 Z 21

;

10

 

 

11

20

 

 

22

1ê

11

 

 

 

 

Y10

 

 

 

 

 

Y20

 

 

 

 

 

 

 

 

Z 22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Y

 

 

1

 

Y

;

 

Y

 

 

 

1

 

Y

 

 

;

 

Y

 

Y

 

 

Y12Y21

.

 

 

 

 

2

ê

 

22

 

 

 

 

 

1ê

 

Z1ê

11

 

 

 

Z 2ê

 

 

 

10

 

11

 

 

Y22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Все приведенные соотношения относятся к комплексным коэффициентам уравнений четырехполюсника. Произведя опыты при различных частотах, экспериментально можно получить частотные характеристики параметров четырехполюсника, которые могут быть использованы для расчета переходных процессов с помощью интеграла Фурье.

13.4. Соединения четырехполюсников и матричная запись уравнений четырехполюсника

Уравнения четырехполюсника, записанные через Y-параметры, в матричной форме имеют вид

 

 

I

 

 

 

Y

Y

 

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

11

 

12

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I 2

 

Y21

Y22

 

 

 

 

 

U

2

,

 

èëè

 

 

 

I

YU,

соответственно, через Z-параметры:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U1

 

 

Z11

 

 

 

 

Z12

 

 

 

 

I1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

2

 

 

Z 21

 

 

 

Z 22

 

 

 

 

I 2

 

,

èëè

 

 

 

U ZI

и через A-параметры:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U1

 

 

 

A B

 

 

 

 

 

U 2

 

 

 

,

 

èëè

 

 

 

 

U1

 

 

 

A

 

 

 

U

2

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I1

 

 

 

C D

 

 

 

 

 

I 2

 

 

 

 

 

 

 

 

 

 

 

 

I1

 

 

 

 

 

 

 

 

I 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Матричная запись уравнений оказывается целесообразной при анализе различных соединений четырехполюсников.

Рассмотрим так называемое к а с к а д н о е с о е д и н е н и е двух четырехполюсников (рис. 13.7). Эти два четырехполюсника, взятые вместе, можно рассмат-

 

ривать как один эквивалентный четы-

 

рехполюсник, обведенный на рис. 13.7

 

штриховой линией, с величинами U1, I1

 

на входе и U 2 , I 2

на выходе. В данном

 

случаеU

U

; I

I

;U

U è I

2

I .

 

1

1

1

1

2

2

2

Ðèñ. 13.7

Задача заключается в определении па-

раметров

эквивалентного четырехпо-

 

люсника через известные параметры первого и второго четырехполюсников.

Равенства U

U è I

I , имеющие место на стыке двух четырехполюсни-

2

1

2

1

ков, определяют выбор целесообразной системы уравнений.

Глава 13. Анализ общих свойств четырехполюсников

177

В матричной форме имеем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

 

 

U

 

 

 

;

 

 

 

 

 

 

 

 

U

 

 

 

 

U

 

 

 

 

 

;

 

 

U

 

 

 

 

 

 

 

 

 

U

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При этом лучше всего использовать запись уравнений через A-параметры:

 

 

 

 

 

 

 

 

 

 

U

 

 

 

 

 

 

A'

 

 

B'

 

 

 

 

 

U

 

 

 

 

;

 

 

 

 

U

 

 

 

 

 

 

 

 

A

B

 

 

 

 

 

 

 

U

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

C

D

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

D'

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Используя эти соотношения, получим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

U

 

 

 

A'

B'

 

 

 

 

 

 

 

U

 

 

 

 

 

A'

 

 

 

 

B'

 

 

 

U

 

 

 

 

A'

B'

 

 

 

A

 

 

 

 

B

 

 

 

 

 

 

 

U

 

 

 

 

 

A

 

 

 

 

 

U

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

C

 

 

 

 

 

 

 

C

 

 

 

 

D

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

 

 

 

I

 

 

 

I

 

 

 

D'

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

D'

 

 

 

I

 

 

 

 

 

 

 

 

 

D'

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

Таким образом, матрица A-параметров двух каскадно соединенных четырехполюсников равна произведению матриц A-параметров отдельных четырехпо-

люсников. Произведя эту операцию, получаем

 

 

 

 

 

 

A

 

 

 

 

 

 

 

A'

 

 

 

 

 

 

 

A

 

 

 

 

 

A' A B' C

A' B B' D

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C A D' C

CB D' D

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрим в качестве другого примера так называемое п а р а л л е л ь н о е

с о е д и н е н и е двух четырехполюсников (рис. 13.8).

 

 

 

 

При таком соединении имеют место равенства U

U

U è U

2

U

U èëè

в матричной форме

 

 

 

 

 

 

 

 

 

 

 

 

1

1

1

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

 

 

U

 

 

 

 

 

U

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

U

 

 

 

 

 

U

 

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

Поэтому в качестве подходящей системы уравнений следует выбрать ту, в которой токи выражаются через напряжения, т. е. систему Y-параметров. Имеем

 

 

 

 

 

I

 

 

Y

 

Y

 

 

 

 

U

 

 

 

è

 

 

I

 

 

 

 

 

 

 

Y

Y

 

 

 

 

 

U

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

11

 

 

12

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

11

 

12

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

Y

Y

 

 

 

 

U

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

Y

Y

 

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

21

 

 

22

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

21

 

22

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Òàê êàê I

I

 

I ;

I

I

I , òî

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

1

 

 

 

1

2

 

 

2

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

I

 

 

 

 

I

 

 

 

 

Y

 

 

Y

 

 

 

 

 

 

 

 

U

 

 

 

 

 

 

 

Y

 

Y

 

 

U

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

1

 

 

 

 

 

11

 

12

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

11

 

12

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

I

 

 

 

 

I

 

 

 

 

Y

 

 

Y

 

 

 

 

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

Y

 

Y

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

 

 

 

2

 

 

 

 

 

 

21

 

22

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

21

 

22

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Имея в виду равенство матриц напряжений, получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

Y

 

Y

 

 

 

 

Y

 

Y

 

 

 

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

Y

 

 

 

Y

 

Y

Y

 

 

 

 

 

 

 

U

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

)

 

11

 

12

 

 

 

11

 

12

 

 

 

,

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11

11

 

 

 

 

 

12

12

 

 

 

 

 

 

 

1

 

 

 

 

I

 

(

 

Y

 

Y

 

 

 

 

Y

 

Y

 

 

 

+

 

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

Y Y

Y Y

 

 

 

 

 

 

 

U

 

 

 

 

 

2

 

 

21

 

22

 

 

 

 

21

 

22

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

21

22

 

 

 

 

 

22

22

 

 

 

 

 

 

 

2

 

 

 

 

 

 

)

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Следовательно, при параллельном соединении четырехполюсников матрица Y-параметров есть сумма матриц Y-параметров отдельных четырехполюсников.

Âзаключение рассмотрим так называемое п о с л е д о в а т е л ь н о е с о е д и -

íе н и е двух четырехполюсников (рис. 13.9). При таком соединении имеем

U

U

U ; U

2

U

U

è

I

I

I ; I

2

I

I .

1

1

1

2

2

 

1

1

1

2

2

178 Часть 2. Теория линейных электрических цепей

Ðèñ. 13.8

Ðèñ. 13.9

При этом целесообразно воспользоваться уравнениями четырехполюсника, записанными через Z-параметры:

 

 

 

 

 

 

 

 

 

 

 

U

 

 

Z

 

 

 

 

Z

 

 

 

 

 

I

;

U

 

 

 

 

 

 

Z

Z

 

 

 

 

I

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

11

 

 

 

12

 

 

 

 

 

 

 

 

1

1

 

 

 

 

 

 

 

 

11

 

12

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

Z

 

 

 

 

Z

 

 

 

 

 

I

 

U

 

 

 

 

 

 

 

Z

Z

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

21

 

 

22

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

21

 

22

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

U

 

 

 

U

 

 

 

Z

Z

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

Z

Z

 

 

I

 

 

 

 

 

Z

Z

Z

Z

 

 

 

 

 

 

 

I

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

1

 

 

11

 

 

12

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

11

12

 

 

1

 

 

 

 

11

11

12

12

 

 

 

 

 

 

 

1

 

 

 

 

U

 

 

 

U

 

 

 

U

 

 

 

Z

Z

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

Z

Z

 

 

I

 

 

 

 

 

Z

Z

Z

Z

 

 

 

 

 

 

 

I

 

 

 

 

 

2

 

 

 

2

 

 

 

2

 

 

 

21

 

 

22

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

21

22

 

 

2

 

 

 

 

 

21

21

22

22

 

 

 

 

 

 

 

2

 

 

 

 

Таким образом, при последовательном соединении двух четырехполюсников матрица Z-параметров эквивалентного четырехполюсника равна сумме матриц Z-параметров отдельных четырехполюсников.

13.5. Передаточные функции четырехполюсников

Часто возникает задача нахождения тока i2(t) или напряжения u2(t) в некотором (втором) участке сложной цепи, возникающих под воздействием заданного тока i1(t) или напряжения u1(t) в другом (первом) участке цепи. Обозначив i1(t) èëè

u1(t) через x1(t), a i2(t) èëè u2(t) через x2(t), введем понятие п е р е д а т о ч н о й ф у н к ц и и K(p) от первого ко второму участку цепи из соотношения

K(p) X 2 (p) ,

X1(p)

ãäå X1(p) è X2(p) — операторные изображения x1(t) è x2(t).

Выделяя эти два участка из общей цепи и имея в виду, что воздействие возмущения x1(t) от первого участка ко второму передается через всю остальную пассивную цепь, можем рассматривать эту остальную цепь как четырехполюсник, и тогда передаточная функция определится параметрами этого четырехполюсника. При этом x1(t) окажется функцией, определяющей возмущение на входе четырехполюсника (на стороне зажимов 1 – 1 ), à x2(t) – функцией, определяемой реакцией на это возмущение на выходе четырехполюсника (на стороне зажимов 2 – 2 ).

Если рассматриваемые функции удовлетворяют требованиям, при которых возможно преобразование Фурье, то, заменяя p íà j , получим

K( j ) K( ) ej X 2 ( j ) .

X1( j )

I1(p) U1(p) ,
Z1âõ (p)

Глава 13. Анализ общих свойств четырехполюсников

179

Если функции x1(t) è x2(t) обе являются токами или обе являются напряжениями, то передаточная функция представляет собой безразмерную величину. Такой случай имеем, например, если x1(t) u1(t) è x2(t) u2(t) суть напряжения на входе и на выходе четырехполюсника.

Åñëè x1(t) u1(t), a x2(t) i2(t), òî K(p) представляет собой обобщенную (операторную) взаимную проводимость между рассматриваемыми участками цепи, а K(j ) — ее частотную характеристику. Наоборот, если x1(t) i1(t), a x2(t) u2(t), òî K(p) — обобщенное (операторное) взаимное сопротивление è K(j ) — его частотная характеристика.

Рассмотрим передаточную функцию четырехполюсника в случае, когда на входе задано напряжение U1, а на выходе включен приемник с сопротивлением Zïð. Имеем

ãäå Z1âõ(p) — операторное сопротивление на входе четырехполюсника, зависящее от параметров четырехполюсника и сопротивления приемника.

Напишем уравнение четырехполюсника через Z-параметры в операторной форме:

U1(p) Z11(p)I1(p) Z12 (p)I 2 (p);

 

 

 

 

U 2 (p) Z 21(p)I1(p) Z 22 (p)I 2 (p).

 

 

 

 

Подставляя в эти уравнения выражение для тока I 2 (p)

U

2

(p)

и исключая

Z ïð (p)

 

 

èç íèõ I1(p), получим

K(p)

U 2 (p)

 

 

 

 

Z 21(p)Z ïð (p)

 

 

.

U

1

(p)

Z

(p)Z

ïð

(p) Z

(p)Z

22

(p) Z

12

(p)Z (p)

 

 

 

11

 

11

 

 

21

 

В частном случае, когда сопротивление приемника равно бесконечности (холостой ход),

K(p) Z 21(p) .

Z11(p)

Такое же значение для K(p) можно принять в важных практических случаях, когда сопротивление приемника, приключаемого к четырехполюснику, очень велико, например, если выходные зажимы четырехполюсника приключаются

êсетке и катоду электронной лампы.

Âслучае если на входе четырехполюсника задан ток I1(p), а не напряжение,

Z21(p) I1(p) + Z22(p) I2(p) è èç

U2(p)/Zïð(p) получаем

K(p)

U 2 (p)

 

Z 21(p)Z ïð (p)

,

I1(p)

Z ïð (p) Z 22 (p)

è ïðè Zïð (холостой ход)

 

 

 

 

K(p) Z 21(p).

180 Часть 2. Теория линейных электрических цепей

Рассмотрим вопрос о расположении в комплексной плоскости полюсов и нулей передаточной функции, т. е. значений комплексной величины p (комплексной частоты), при которых передаточная функция обращается в или в 0. Для определенности будем рассматривать передаточную функцию как отношение напряжений на выходе и входе четырехполюсника при холостом ходе, т. е. вели-

÷èíó K(p) Z21(p)/Z11(p).

Рассуждения легче вести в отношении свойств входных сопротивлений Z10

èZ20 при холостом ходе, определенных со стороны первичных и вторичных зажимов, и сопротивления Z1ê при коротком замыкании во вторичной цепи, как имеющих определенный физический смысл. Поэтому выразим величины Z21(p)

èZ11(p) через эти входные сопротивления, представленные в операторной форме.

§ 13.3 были приведены соотношения

Z10 (p) Z11(p); Z

20 (p) Z

22 (p); Z

1ê (p) Z

11(p)

Z

12

(p)Z 21

(p)

.

 

 

Z

22 (p)

 

 

 

 

 

 

 

 

Отсюда получаем

Z 21(p) 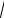Z 20 (p)[Z10 (p) Z1ê (p)] è Z11(p) Z10 (p).

Величины Z10(p), Z20(p), Z1ê(p) имеют и полюсы, и нули только в левой полуплоскости комплексной переменной p. Их нули находятся только слева от оси мнимых. Это вытекает из следующих соображений: закон Ома в операторной форме, например при подаче напряжения на первичные зажимы при холостом ходе, имеет вид

I10 (p) U10 (p) Y10 (p)U10 (p).

Z10 (p)

Åñëè u10(t) есть импульс напряжения с площадью A, то его операторное изо-

бражение U10(p) A. В этом случае полюсы Y10(p), ò. å. íóëè Z10(p), являются одновременно и полюсами I10(p).

В § 10.6 было показано, что полюсы операторного изображения свободной составляющей тока для пассивных электрических цепей могут лежать только в левой полуплоскости, так как вещественная часть корней характеристического уравнения должна быть отрицательной, ибо процесс должен быть затухающим. В данном случае после воздействия импульса весь ток и будет только свободным. Из этих рассуждений вытекает, что все нули величины Z10(p), а следовательно, и полюсы Y10(p) лежат в левой полуплоскости. То же самое относится к вели-

чинам Z20(p) è Z1ê(p).

Рассматривая закон Ома в форме

U10 (p) I10 (p) Z10 (p)I10 (p) Y10 (p)

и проводя аналогичные рассуждения по отношению к импульсу тока, приходим к выводу, что все полюсы Z10(p) è, соответственно, íóëè Y10(p) также лежат в левой полуплоскости.

Ðèñ. 13.10
Ðèñ. 13.11

Глава 13. Анализ общих свойств четырехполюсников

181

Рассмотрим положение полюсов передаточной функции K(p). Они определяются полюсами числителя Z 21(p) 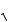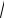Z 20 (p)[Z10 (p) Z1ê (p)] и нулями знаменателя Z11(p) Z10(p). И те, и другие лежат только в левой полуплоскости, что следует из только что приведенных рассуждений о расположении полюсов и нулей входных сопротивлений. Таким образом, приходим к важному положению, что

все полюсы передаточной функции пассивного четырехполюсника лежат в левой полуплоскости.

Рассмотрим положение нулей передаточной функции K(p). Они определяются нулями Z21(p) и полюсами знаменателя. Последние лежат только в левой полуплоскости, однако в отношении нулей Z21(p) такое заключение сделать нельзя. В выражение под корнем входит разность [Z10(p) – Z1ê(p)], которая может содержать нули как в левой, так и в правой полуплоскости, в чем убедимся сейчас на примерах. В таком случае нули передаточной функции пассивного четырехполюсника могут лежать и в левой, и в правой полуплоскости.

Рассмотрим схему цепи, изображенную на рис. 13.10, называемую иногда л е с т н и ч н о й. Нуль передаточной функции, т. е. нулевое значение U2(p) при конечном U1(p), как видно из схемы, может быть либо когда вели- чины Z2(p), èëè Z4(p), èëè Z6(p) равны нулю, т. е. имеют нуль, либо когда величины Z1(p), èëè Z3(p), èëè Z5(p), èëè Z7(p) равны бесконечности, т. е. имеют полюс. Но и нули, и полюсы всех этих величин лежат в левой полуплоскости, а следовательно, и все нули передаточной функции цепи также лежат в левой полуплоскости.

Рассмотрим теперь схему цепи, изображенную на рис. 13.11, иногда называемую с к р е щ е н н о й или м о с т о в о й.

Как нетрудно заметить, при холостом ходе эта цепь состоит из двух парал-

 

 

 

1

 

1

 

лельно включенных ветвей r, L, Ñ, а следовательно, Z

 

(p)

r pL

.

10

 

 

 

2

 

 

 

 

 

 

pC

Вследствие симметрии Z20(p) Z10(p). При коротком замыкании зажимов 2–2 оказываются последовательно включенными два одинаковых контура, каждый из которых состоит из параллельно включенных ветви (L, Ñ) и ветви r, ò. å.

 

 

 

 

 

 

 

Z

 

2

r [pL 1 (pC)]

.

 

 

 

 

 

 

 

 

 

 

 

1ê

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r pL 1 (pC)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Используя эти выражения, получим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

1

 

 

 

 

 

Z

 

 

(p) Z

 

 

(p)

 

r pL

 

;

 

 

 

 

11

10

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Z

 

(p)

 

Z

 

(p)[Z

 

 

(p) Z

 

(p)]

r pL

 

21

 

20

10

1ê

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pC

и, следовательно,

Ðèñ. 13.12

182 Часть 2. Теория линейных электрических цепей

K(p)

Z

21

(p)

 

r pL 1

(pC)

 

 

p2 2−p 2

 

 

 

 

 

 

 

 

 

 

 

 

0

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Z11(p) r pL 1

(pC)

 

 

p2 2−p 02

 

ãäå − r/(2L), 2 1/(LC).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Полюсы K(p) расположены в точках p

1,3

−

 

− 2

2 , т. е. оба в левой по-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

луплоскости.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Íóëè K(p) расположены в точках p

2,4

 

− − 2 2

в правой полуплоскости.

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

Четырехполюсники, все нули передаточной функции которых расположены в левой полуплоскости, называются м и н и м а л ь н о - ф а з о в ы м и. Примером их является цепь, схема которой приведена на рис. 13.10.

Четырехполюсники, имеющие нули также и в правой полуплоскости, называются н е м и н и м а л ь н о - ф а з о в ы м и . Примером их является цепь, изображенная на рис. 13.11. Эта цепь обладает интересными и важными свойствами.

Пусть

0

> −ϑ ò. å. p

1,3

–− ± j è p

2,4

− ± j , ãäå ' 2

− 2 . Тогда

 

 

 

 

 

0

 

 

 

 

 

K(p)

(p p2 )(p p4 )

.

 

 

 

 

 

 

 

 

 

 

 

 

 

(p p )(p p

3

)

 

 

 

 

 

 

 

 

 

1

 

 

 

Для перехода от этого выражения к частотной характеристике передаточной функции следует принять p j . Получаем

K( j ) ( j p2 )( j p4 ) . ( j p1)( j p3 )

Комплексным величинам, стоящим в скобках в числителе и знаменателе, соответствуют векторы, начинающиеся в точках p1, p2, p3, p4 и кончающиеся в переменной точке p j на оси мнимых (рис. 13.12).

Из рисунка легко видеть, что модуль K( ) 1 и остается неизменным при изменении частоты от нуля до бесконечности. Аргумент K(j ) равен сумме аргументов множителей числителя, за вычетом суммы

аргументов множителей знаменателя, т. е. ( 2 + 4) – ( 1 + 3) 2# – 2( 1 + 3).

При изменении частоты от 0 до аргумент передаточной функции изменяется от 2# äî 0, òàê êàê ( 1 + 3) изменяется от 0 до #.

Независимость модуля K(j ) от частоты и является ценным свойством этой цепи. Подключая каскадно эту цепь к некоторому четырехполюснику, получаем возможность изменять фазочастотную характеристику последнего, не изменяя его амплитудно-частотной характеристики.

Из сказанного видно, что для цепи, изображенной на рис. 13.11, отсутствует зависимость между фазочастотной и амплитудно-частотной характеристиками передаточной функции, так как фаза изменяется, а амплитуда остается неизменной при изменении частоты. Отсутствие такой связи характерно для немини-

Соседние файлы в предмете Электрооборудование подстанций промышленных предприятий
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности