9. Деформации бетона при длительном загружении, ползучесть бетона.

Д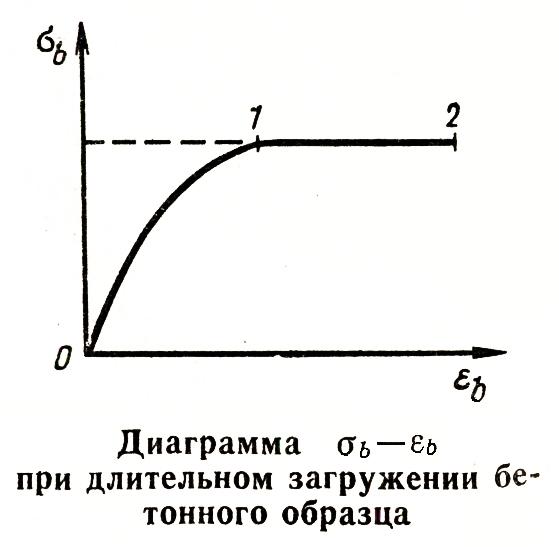еформации при длительном действии нагрузки. Придлительном действии нагрузки неупругие деформации бетона с течением времени увеличиваются. Наибольшая интенсивность нарастания неупругих деформаций наблю­дается первые 3 – 4 мес и может продолжаться несколь­ко лет. На диаграмме σ_b – ε_b участок 0 – 1 характеризует деформации, возникающие при загружении, кривизна этого участка зависит от скорости загружения; участок 1–2 характеризует нарастание неупругих деформаций при постоянном значении напряжений.

Свойство бетона, характеризующееся нарастанием не­упругих деформаций при длительном действии нагруз­ки, называют ползучестью бетона.

Деформации ползуче­сти могут в 3 – 4 раза превышать упругие деформации. При длительном действии постоянной нагрузки, если де­формации ползучести нарастают свободно, напряжения в бетоне остаются постоянными. Если же связи в бето­не (например, стальная арматура) стесняют свободное развитие ползучести, то ползучесть будет стесненной, при которой напряжения в бетоне уже не будут оста­ваться постоянными.

Если бетонному образцу сообщить некоторое началь­ное напряжение σ_b⁰ и начальную деформацию ε_b⁰ , а за­тем устранить возможность дальнейшего деформирова­ния наложением связей, то с течением времени напря­жения в бетоне начинают уменьшаться.

Свойство бето­на, характеризующееся уменьшением с течением време­ни напряжений при постоянной начальной деформации, называют релаксацией напряжений.

Ползучесть и релаксация имеют общую природу и оказывают существенное влияние на работу железобе­тонных конструкций под нагрузкой.

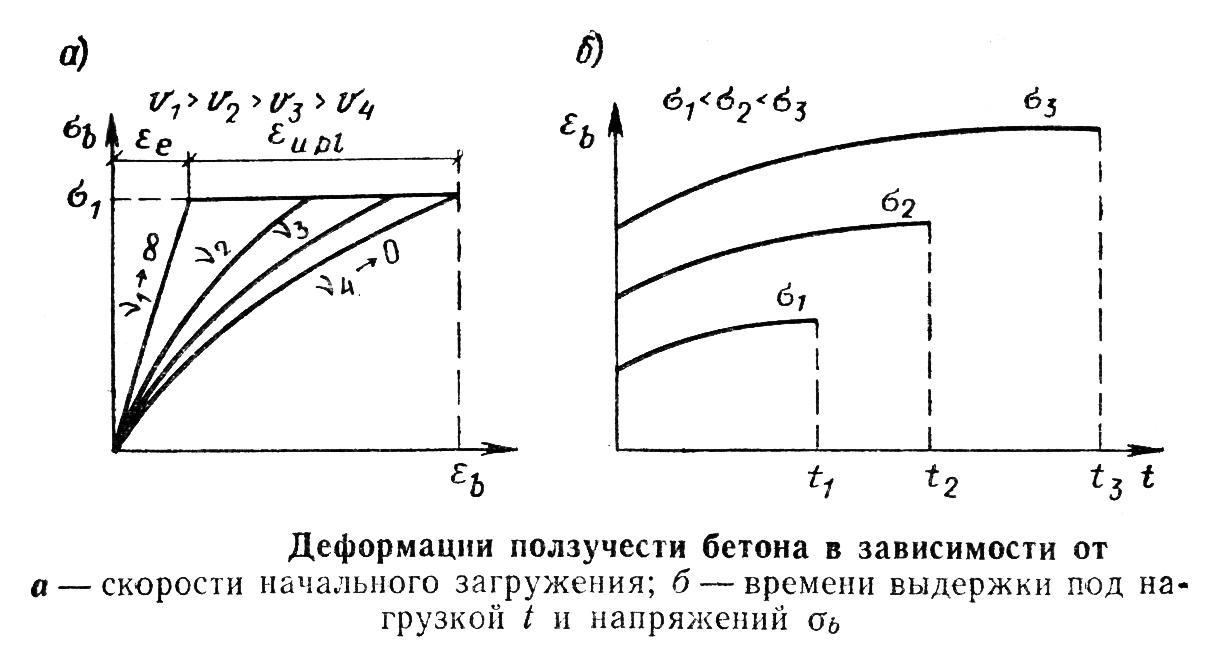
Опыты с бетонными призмами показывают, что независимо от того, с какой скоростью загружения v было получено напряжение σ_b1, конечные деформации ползу­чести, соответствующие этому напряжению, будут оди­наковыми (рис. а). С ростом напряжений ползу­честь бетона увеличивается; зависимость деформации— время при напряжениях σ_b1< σ_b2< σ_b3 показана на рис. б. Загруженный в раннем возрасте бетон обладает большей ползучестью, чем старый бетон. Ползучесть бе­тона в сухой среде значительно больше, чем во влажной. Технологические факторы также влияют на ползучесть бетона: с увеличением W/C и количества цемента на еди­ницу объема бетонной смеси ползучесть возрастает; с повышением прочности зерен заполнителей- ползучесть уменьшается; с повышением прочности бетона, его класса ползучесть уменьшается. Бетоны на пористых за­полнителях обладают несколько большей ползучестью, чем тяжелые бетоны.

Природа ползучести бетона объясняется его структу­рой, длительным процессом кристаллизации и уменьше­нием количества геля при твердении цементного камня. Под нагрузкой происходит перераспределение напряже­ний с испытывающей вязкое течение гелевой структур­ной составляющей на кристаллический сросток и зерна заполнителей. Одновременно развитию деформаций пол­зучести способствуют капиллярные явления, связанные с перемещением в микропорах и капиллярах избыточной воды под нагрузкой. С течением времени процесс пере­распределения напряжений затухает и деформирование прекращается.

Ползучесть разделяют на линейную, при которой за­висимость между напряжениями и деформациями при­близительно линейная, и нелинейную. При напряжениях, превышающих границу образования структурных микро­трещин R⁰_crc , начинается ускоренное развитие деформа­ций, или нелинейная ползучесть. Такое разделение пол­зучести условно, так как в некоторых опытах наблюда­ется нелинейная зависимость σ_b – ε_b даже при относи­тельно малых напряжениях. Отметим здесь существенно важное значение учета нелинейной ползучести для прак­тических расчетов предварительно напряженных изгиба­емых, внецентренно сжатых и некоторых других элемен­тов.

П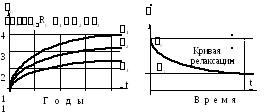олзучесть и усадка бетона развиваются совместно. Поэтому полная деформация бетона представляет со­бой сумму деформаций: упругойε_е, ползучести ε_pl и усадки ε_sl. Однако в то время как усадка носит харак­тер объемной деформации, ползучесть развивается глав­ным образом в направлении действия усилия.

Ползучесть бетона - это явление увеличения неупругих деформаций при длительном действии нагрузки

Абсолютные деформации ползучести зависят от возраста бетона, его прочности, уровня напряжений, гранулометрического состава и т.д. Различают линейную и нелинейную ползучесть. При линейной ползучести прирост неупругих деформаций за единицу времени пропорционален приложенным напряжениям, при нелинейной ползучести такая зависимость отсутствует.

Мера ползучести.

Под мерой ползучести С_b понимают относительную деформацию ползучести приσ_b ≤ 0,3R_bn, накопившуюся к моменту времениtпри загружении образцов вt₀ < tи приходящуюся на 1 МПа действующего постоянного напряжения.

C_b(t, t₀) = ε_cr (t, t₀)/ σ_b, ε_cr = λ_вε_b σ_b = ε_b∙E^!_b

Релаксация -это процесс уменьшения напряжений при постоянной деформации.

Ползучесть и релаксации взаимосвязаны. Они увеличивают прогибы, снижают предварительное напряжение, уменьшают трещиностойкость.