Математическая формулировка

В математической формулировке для магнитостатики теорема имеет следующий вид:

Здесь  — вектор магнитной индукции,  — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме:

Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса.

Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие в веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты микрочастиц (см.например ферромагнетики).

Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величину намагниченности и введя вектор напряжённости магнитного поля

Тогда теорема о циркуляции запишется в форме^[6]

где под (в отличие от в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку  — это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить)^[7].

В динамическом случае — то есть в общем случае классической электродинамики— когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идет об обобщенной теореме, включающей , — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене .

Обобщение

Основным фундаментальным обобщением теоремы является четвёртое уравнение Максвелла. В интегральной форме оно является прямым обобщением на динамический случай магнитостатической формулы, приведённой выше. Для вакуума^[9]:

для среды:

(Как видим, формулы отличаются от приведенных выше только одним добавочным членом со скоростью изменения электрического поля в правой части).

Дифференциальная форма этого уравнения:

(в гауссовой системе, для вакуума и среды соответственно) — также можно при желании считать вариантом обобщения теоремы о циркуляции магнитного поля, поскольку она, конечно, тесно связана с интегральной.

Практическое значение

Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам^[1]. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:

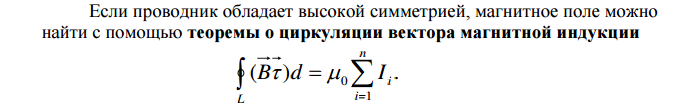
5. Элементарный контур с током – магнитный диполь, его магнитный момент. Сила и момент силы, действующий на диполь, помещенный во внешнее магнитное поле

Диполь — идеализированная система, служащая для приближенногоописания распространения поля. Дипольное приближение основано наразложении потенциалов поля в ряд по степеням радиус-вектора иотбрасывании всех членов выше первого порядка. Полученные функциибудут эффективно описывать поле в случае если

Размеры излучающей поле системы малы по сравнению срассматриваемыми расстояниями, так что отношение характерного размерасистемы к длине радиус-вектора является малой величиной и имеет смыслрассмотрение лишь первых членов разложения потенциалов в ряд.

Член первого порядка в разложении не равен 0, в противном случае нужноиспользовать приближение более высокой мультипольности.

В уравнениях рассматриваются градиенты потенциалов не выше первогопорядка.

Типичный пример диполя — два бесконечно близких заряда, равных повеличине и противоположных по знаку. Поле такой системы полностьюописывается дипольным приближением.

Электрический диполь — идеализированная электронейтральная система, состоящая из точечных иравных по абсолютной величине положительного и отрицательного электрических зарядов.

Другими словами, электрический диполь представляет из себя совокупность двух равных по абсолютнойвеличине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга

Произведение вектора , проведённого от отрицательного заряда к положительному, на абсолютнуювеличину зарядов , называется дипольным моментом: .

Во внешнем электрическом поле на диполь действует момент сил , который стремится повернутьего так, чтобы дипольный момент развернулся вдоль направления поля. Потенциальная энергия диполя вэлектрическом поле равна .

Вдали от диполя напряжённость его электрического поля убывает с расстоянием R как 1 / R³, то естьбыстрее, чем у точечного заряда.

Любая электронейтральная система в некотором приближении может рассматриваться как электрическийдиполь с моментом , где  — заряд i-го элемента,  — его радиус-вектор. При этомдипольное приближение будет корректным, если расстояние, на котором изучается электрическое полесистемы, велико по сравнению с её характерными размерами.