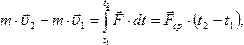1) Основные кинематические параметры точки: траектория, ее радиус кривизны: мгновенные радиус-вектор точки, скорость, ускорение, нормальное, тангенциальное ускорение; средние (на интервале) значения. Определение этих понятий и связь между ними 2) Наложение (сложение) движений, преобразование Галилея, теорема Кенига. 3) Инерциальные системы отсчета и закон динамики поступательного движения тела в них. Закон динамики центра масс системы материальных точек в инерциальных системах координат, разделение сил на внутренние и внешние. 4) Закон динамики вращательного движения твердого тела вокруг заданной оси в инерциальных системах координат и в «системах центра масс». Момент инерции, теорема Штейнера. Момент количества движения, момент силы (практическое вычисление – знать плечо, линию действия силы, линию импульса). 5) Три закона сохранения в механике и условия их применимости, плюс соотношение для изменения энергии системы с учетом работы неконсервативной силы. 6) Определение электрического и магнитного поля (через силы Лоренца, Ампера). Знать два уравнения Максвелла для макроскопических полей E и D (в присутствие диэлектриков) и два для B и H (в присутствие магнетиков) в статическом случае, в интегральном виде. Знать соотношения связи между основным и вспомогательным полем («материальные уравнения»). Соответственно, уметь рассчитать поле для простой геометрии (например, бесконечно-длинного кругового цилиндра). 7) Элементарный электрический диполь, сила и момент силы, действующие на него во внешнем поле. Диэлектрик, вектор поляризованности диэлектрика (и теорма Гаусса для него). 8) Потенциал электростатического поля, связь с вектором напряженности, изопотенциальные поверхности и силовые линии поля. Потенциальная энергия системы зарядов. 9) Закон Био-Саварра-Лапласа для магнитного поля (хорошо бы - в сравнении с электрическим полем точечного заряда). 10) Элементарный магнитный диполь, Магнетик, намагниченность магнетика. Теорема о циркуляции намагниченности магнетика. 11) Закон электромагнитной индукции = уравнение Максвелла для циркуляции электрического поля в общем (нестационарном) случае (как для деформирующегося контура, так и для переменного магнитного поля).

1)

Радиус-вектор — вектор, определяющий положение материальной точки в пространстве: . Здесь  — координаты радиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат ) от времени называется законом движения. Траектория — это линия вдоль которой движется материальная точка. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:

,

Где : — модуль начальной скорости, а— Тангенциальное ускорение.

Описание движения при помощи понятия траектории — один из ключевых моментов классической механики . В квантовой механике движения носит бестраекторный характер, а значит само понятие траектория теряет смысл.

Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:

.

Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.

Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:

.

Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:

.

Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:

.

Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории.

Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:

.

Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:

.

Здесь — единичныйвектор нормали, — единичный вектор касательной. Величинаназываетсянормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:

.

В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.

Величина называетсятангенциальным ускорением и характеризует величину изменения модуля скорости:

.

2)

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей^[1].

Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

Преобразова́ния Галиле́я — в классической механике (механике Ньютона) и нерелятивистской квантовой механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой^[1]. Термин был предложен Филиппом Франком в 1909 году.^[2] Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время»^[3]).

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.

• Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, можно считать во многом определяющим структуру ньютоновской механики. Вместе же с такими дополнительными идеями, как симметрия пространства и принцип суперпозиции в том или ином виде (утверждающий эквивалентность взаимодействия многих тел в малый промежуток времени композиции воображаемых последовательных попарных взаимодействий этих тел), преобразования Галилея могут быть практически достаточным основанием для формулировки ньютоновской механики (вывода ее основных законов).

Вид преобразований при коллинеарных осях

Если ИСО S' движется относительно ИСО S с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

или, используя векторные обозначения,

(последняя формула остается верной для любого направления осей координат).

• Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

• Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей (много меньше скорости света).

Формула преобразования скоростей

Достаточно продифференцировать в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор , где радиус-вектор какого-то тела A в системе отсчета K обозначим за , а в системе отсчета K'  — за , подразумевая, как всегда в классической механике, что время в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени: .

Тогда в любой момент времени

и в частности, учитывая

,

имеем: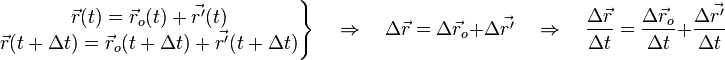

где:

 — средняя скорость тела A относительно системы K;

 — средняя скорость тела А относительно системы K' ;

 — средняя скорость системы K' относительно системы K.

Если то средние скорости совпадают с мгновенными: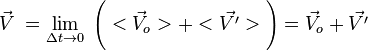

или короче

— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета.

(Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:

Теоре́ма Кёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс. 

Формулировка

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где  — полная кинетическая энергия системы,  — кинетическая энергия движения центра масс,  — относительная кинетическая энергия системы^[2].

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.

Вывод

Приведём доказательство теоремы Кёнига для случая, когда массы тел, образующих механическую систему ,  распределены непрерывно^[3].

Найдём относительную кинетическую энергию системы ,  трактуя её как кинетическую энергию, вычисленную относительно подвижной системы координат. Пусть  — радиус-вектор рассматриваемой точки системы   в подвижной системе координат. Тогда^[4]:

где точкой обозначено скалярное произведение, а интегрирование ведётся по области пространства, занимаемой системой в текущий момент времени.

Если  — радиус-вектор начала координат подвижной системы, а  — радиус-вектор рассматриваемой точки системы   в исходной системе координат, то верно соотношение:

Вычислим полную кинетическую энергию системы в случае, когда начало координат подвижной системы помещено в её центр масс. С учётом предыдущего соотношения имеем:

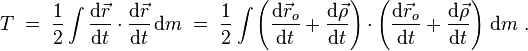
Учитывая, что радиус-вектор одинаков для всех , можно, раскрыв скобки, вынести за знак интеграла:

Первое слагаемое в правой части этой формулы (совпадающее с кинетической энергией материальной точки, которая помещена в начало координат подвижной системы и имеет массу, равную массе механической системы) может интерпретироваться^[2] как кинетическая энергия движения центра масс.

Второе слагаемое равно нулю, поскольку второй сомножитель в нём получается дифференцированием по времени произведения радиус-вектора центра масс на массу системы^[5], но упомянутый радиус-вектор (а с ним и всё произведение) равен нулю:

так как начало координат подвижной системы находится (по сделанному предположению) в центре масс.

Третье же слагаемое, как было уже показано, равно , т. е. относительной кинетической энергии системы .

3)

Первый закон Ньютона

Динамика – раздел механики, в котором изучается движение тел с учетом причин, вызывающих или изменяющих это движение. Классическая динамика базируется на трех законах Ньютона.

Первый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции, а движение тела, свободного от внешних воздействий – движением по инерции.

Система отсчета, в которой справедлив закон инерции, называется инерциальной системой отсчета. Всякая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, является также инерциальной системой отсчета.

Инерциальная система отсчета может рассматриваться как модель, к которой реальная система отсчета имеет ту или иную степень приближения. Достаточно близка к инерциальной системе отсчета гелиоцентрическая система, начало которой совпадает с центром масс Солнечной системы, а оси координат направлены на три звезды.

Сила

 

Для описания механического действия тел друг на друга вводят понятие силы. Силой, действующей на тело, называют физическую величину, являющуюся мерой механического действия на это тело со стороны какого-либо другого тела, в результате которого тело приобретает ускорение или изменяет форму и размеры.

Механическое взаимодействие может осуществляться как между непосредственно контактирующими телами (например, при ударе, трении, давлении друг на друга и т. п.), так и между удаленными телами.

Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем или просто полем.

Взаимодействие между удаленными телами осуществляется посредством связанных с ними гравитационных и электромагнитных полей.

Пользуясь понятием силы, в механике обычно говорят о движении и деформации рассматриваемого тела под действием приложенных к нему сил. При этом конечно, каждой силе всегда соответствует какое-то определенное тело или поле, действующее с этой силой.

Сила F полностью задана, если указаны ее модуль F, направление в пространстве и точка приложения.

Прямая, вдоль которой направлена сила, называется линией действия силы. Центральными называются силы, которые всюду направлены вдоль прямых, проходящих через одну и ту же неподвижную точку - центр сил, и зависят только от расстояния до центра сил.

Поле, действующее на материальную точку с силой F, называется стационарным полем, если оно не изменяется с течением времени.

Единица силы - ньютон (Н): 1Н - сила, которая массе в 1кг сообщает ускорение 1м/с² в направлении действия силы.

Если на тело действуют одновременно n сил …приложенных в одной и той же точке A тела, тоn сил можно заменить одной силой , равной их геометрической сумме

(2.1.1)

 

где -результирующая или равнодействующая сила.

Масса. Второй закон Ньютона

Эксперимент показывает, что под действием силы свободное тело изменяет скорость своего поступательного движения, приобретая ускорениеВторой закон Ньютона справедлив в инерциальной системе отсчета и устанавливает связь между ускорением тела и силами, действующими на него: ускорение, приобретаемое телом, пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально его массет

 

.

(2.1.2)

 

В ньютоновской механике, в основе которой лежат законы Ньютона, масса тела характеризует инерционные свойства тела, не зависит от положения тела в пространстве, его скорости, действия на тело других тел и т.д. Масса является величиной аддитивной, т.е. масса тела равна сумме масс всех его частей. Однако свойство аддитивности утрачивается при скоростях, близких к скорости света в вакууме, т.е. в релятивистской механике. За основную единицу массы, называемую килограммом (кг), принимают массу эталонного тела, хранящегося в международном бюро мер и весов.

Уравнение (2.1.2) описывает изменение движения протяженного тела под действием силы только при условии, что тело: 1) не деформируется, и 2) движется поступательно. В противном случае ускорения разных точек тела неодинаковы, и изменение движения всего тела (системы материальных точек) нельзя описать с помощью единого ускорения . Для материальной точки условия 1) и 2) всегда выполняются, и поэтому формулу (2.1.3) называютосновным уравнением динамики материальной точки.

Если на материальную точку действуют несколько сил, то где(2.1.1):

 

.

(2.1.4)

 

Таким образом, если на материальную точку одновременно действуют несколько сил, то каждая из них сообщает материальной точке такое же ускорение, как если бы других сил не было – формулировка принципа независимости действия сил.

 

Импульс материальной точки

 

Импульсом или количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость:

Единица измерения импульса - .

Импульс является одной из важнейших динамических характеристик, зависящей как от быстроты движения материальной точки, так и от ее инертности. Используя выражение (1.1.9) можно показать, что:

С другой стороны, согласно (2.1.2), Следовательно

 

(2.1.5)

 

Уравнение (2.1.5) является одним из математических выражений второго закона Ньютона: скорость изменения импульса материальной точки равна силе, действующей на точку. Из (2.1.6) следует, что где-элементарный импульс силы за малый промежуток времени dt. Таким образом, изменение импульса материальной точки за малый промежуток времени dt равно элементарному импульсу результирующей силы (за тот же промежуток времени), действующей на материальную точку.

Соответственно изменение импульса материальной точки за время от t₁ до t₂: - импульс силы за это же время. Еслито- линейная функция от времени t:

 

(2.1.6)

 

где υ₀ – начальная скорость материальной точки (при t = 0). При Из (2.1.6) следует, что за промежуток времениDt = t₂ - t₁

 

(2.1.7)

 

Если то

 

(2.1.8)

где -среднее значение переменной силы за промежуток времени Dt.

Третий закон Ньютона. Движение центра инерции

Механическое воздействие двух тел друг на друга всегда представляет собой их взаимодействие. На основе количественного анализа механического взаимодействия тел Ньютон установил свой третий закон динамики, который гласит: действия двух тел друг на друга всегда равны и направлены по одной прямой в противоположные стороны, то есть

 

(2.1.9)

 

Здесь - сила, действующая на тело 1 со стороны тела 2, а- наоборот, соответственно (рис.2.1). Третий закон Ньютона является существенным дополнением к первому и второму законам Ньютона.

 

В механике Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс.

Центром инерции или центром масс системы материальных точек называют такую точку C, радиус - вектор которой определяется следующим выражением:

 

(2.1.10,а)

 

где и- масса и радиус-векторi-ой материальной точки системы; m – общая масса всей системы; n – число материальных точек в системе. Соответственно декартовые компоненты центра масс равны:

 

(2.1.10,б)

 

Найдем скорость движения центра инерции системы:

 

(2.1.11)

 

Геометрическую сумму импульсов всех материальных точек системы называют импульсом системы  : Следовательно, из (2.1.11)

 

(2.1.12)

 

Тела, не входящие в состав рассматриваемой механической системы, называют внешними, а силы, действующие на систему со стороны этих тел – внешними силами. Силы взаимодействия между телами системы называют внутренними силами. Если - сила, действующая наi-ую материальную точку со стороныk-ой, то результирующая со стороны всех внутренних сил, приложенных к i-ой точке, равна:

 

(2.1.13)

 

В уравнении (2.1.13) k пробегает значения от 1 до n, кроме i, так как i-ая точка не может действовать сама на себя.

Пусть на i-ую материальную точку действует внешняя сила , при этом по второму закону Ньютона (2.1.6) для системы материальных точек можно записать следующие уравнения:

 

…………………………………………..

(2.1.14)

 

Складывая почленно уравнения (2.1.14), и группируя попарно силы и, можно получить:Согласно третьему закону Ньютона (2.1.9)и, как следствие,- называютглавным вектором внешних сил. С другой стороны, , то есть

 

(2.1.15,а)

 

Уравнение (2.1.15,а) называют основным уравнением динамики поступательного движения системы материальных точек, которое показывает, что скорость изменения импульса механической системы равна главному вектору всех внешних сил, действующих на эту систему. В проекциях на декартовые оси выражение (2.1.15,а) примет вид:

 

(2.1.15,б)

 

В (2.1.15,б) С помощью уравнения (2.1.12) можно переписать (2.1.15,а)

 

или

(2.1.16)

где -ускорение центра инерции. Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы, и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.

В общем случае движение твердого тела можно рассматривать как сумму двух движений: 1) поступательного со скоростью, равной скорости центра масс, и 2) вращательного вокруг центра инерции (С). Поэтому уравнение (2.1.16) часто называют основным уравнением динамики поступательного движения твердого тела.

Закон сохранения импульса

Механическую систему называют замкнутой или изолированной, если на нее не действуют внешние силы, то есть если она не взаимодействует с внешними телами. Для замкнутой системы главный вектор внешних сил тождественно равен нулю. Поэтому из выражения (2.1.15,а) следует закон, который называютзаконом сохранения импульса: импульс замкнутой системы не изменяется с течением времени, то есть

 

и

(2.1.17)

 

где и- масса и скоростьi-ой материальной точки системы. Так как из (2.1.12) известно, что то, используя уравнение (2.1.17), можно показать, что при любых процессах, происходящих в замкнутой системе, скорость ее центра инерции сохраняется неизменной.

Если система не замкнута, но главный вектор внешних сил , то уравнение (2.1.17) справедливо и в открытой системе. Обычно приходится иметь дело с незамкнутыми системами, для которыхи, как следствие,Однако если проекция главного вектора внешних сил на какую-либо ось, неподвижную относительно инерциальной системы отсчета, тождественно равна нулю, то проекция на эту же ось вектора импульса системы не зависит от времени. Например, если = 0, то и, следовательно,р_x = const – закон сохранения проекции импульса.

При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации или в так называемую внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением температуры. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий.

Рассмотрим применение закона сохранения импульса (2.1.17) на примере удара двух тел.

Ударом называется явление изменения скорости тел на конечные величины за очень малый промежуток времени, происходящее при столкновении тел. Общую нормаль к поверхностям соударяющихся тел в точке их соприкосновения называют линией удара. Удар называют прямым, если перед ударом скорости центров инерции соударяющихся тел параллельны линии удара. Удар называют центральным, если центры инерции соударяющихся тел лежат на линии удара.

Прямой центральный удар называют абсолютно неупругим, если после удара тела движутся как одно целое (рис.2.2). Если скорости двух тел до удара соответственно равны –  и  , а массы их определяются значениями m₁ и m₂, то общая скорость тел после абсолютно неупругого удара , согласно уравнению (2.1.17), может быть представлена в виде:

 

(2.1.18)

Масса системы. Центр масс.

Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему

В однородном поле тяжести, для которого g=const, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:

В полученные равенства входят только массы  материальных точек (частиц), образующих тело, и координаты  этих точек. Следовательно, положение точки С (x_C, y_C, z_C) действительно харак­теризует распределение масс в теле или в любой механической си­стеме, если под  понимать соответственно массы и координаты точек этой системы.

Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.

Положение центра масс определяется его радиус-вектором 

где  - радиус-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тя­жести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тя­жести, по существу имеет смысл только для твердого тела, находя­щегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная си­стема под действием каких-нибудь сил или нет.  

4)

Динамика вращательного движения.

Рассмотрим вращение абсолютно твердого тела вокруг неподвижной оси ОО (рис.2). Твердое тело можно рассматривать как систему материальных точек, каждая из которых движется по окружности с одинаковой для всех точек угловой скоростью.

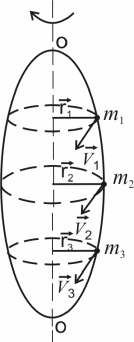
Рис.2

 

Линейная скорость движения каждой точки определяется выражением

V = ωr,                            

где r – расстояние от точки до оси вращения.

 

Момент инерции тела относительно оси. Радиус инер­ции.

Положение центра масс характеризует распределение масс системы не полностью. Например (рис.3), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).

Рис.3

 

Поэтому в механике вводится еще одна характеристика распре­деления масс - момент инерции. Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

Момент инерции имеет размерность [кг∙м²]

Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.

Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.

Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является ме­рой инертности тела при вра­щательном движении и зависит от распределения массы тела относительно оси вращения.

Согласно формуле момент инерции тела равен сумме момен­тов инерции всех его частей от­носительно той же оси. Для од­ной материальной точки, нахо­дящейся на расстоянии h от оси, .

Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина , определяемая равенством

где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.

В случае сплошного те­ла, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве , обратится в интеграл. В результате, учи­тывая, что , где  - плотность, а V - объем тела, получим

  или 

Интеграл здесь распространяется на весь объем V тела, а плотность  и расстояние h зависят от координат точек тела.

Моменты  инерции некоторых однородных тел:

1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относи­тельно оси Аz, перпендикулярной к стержню и прохо­дящей через его конец А (рис.4).

Рис.4

 

Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса , где  - масса единицы длины стержня. В результате

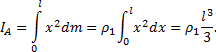
Заменяя здесь ρ₁ его значением, найдем окончательно:

А момент инерции тонкого однородного стержня длины l и массы М относительно оси проходящего через середину и перпендикулярную стержню равен

2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.4,а). Так как все точки кольца находятся от оси Cz на расстоянии h_k=R, то

Следовательно, для кольца .

Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относитель­но ее оси.

3. Круглая однородная пластина или цилиндр ра­диуса R и массы М. Вычислим момент инерции круглой пла­стины относительно оси Сz, перпендикулярной к пластине и прохо­дящей через ее центр (см. рис.5,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.5,б).

              

Рис.5

 

Площадь этого кольца равна , а масса  где - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет

,

а для всей пластины  . Заменяя здесь  его значением, найдем окончательно  

Такая же формула получится, очевидно, и для момента инерции  однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.5,в).

4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:

а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у - вдоль BD):

б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):

г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра): .

 

Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса-Штейнера.

Моменты инерции данного тела относи­тельно разных осей будут, вообще говоря, разными. Покажем, как зная момент инерции относительно какой-нибудь одной оси, проведен­ной в теле, найти момент инерции от­носительно любой другой оси, ей па­раллельной.

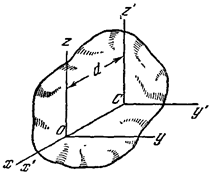
Рис.6

 

Проведем через центр масс С тела произвольные оси Cx'y'z', а через лю­бую точку О на оси Сх' - оси Oxyz, такие, что Оy||Сy', Oz||Cz' (рис.6). Расстояние между осями Cz' и Оz обозначим через d. Тогда  

но, как видно из рисунка, для любой точки тела  или  , а . Подставляя эти значения , в выражение для  и вынося общие множители d ² и 2d за скобки, получим

В правой части равенства первая сумма равна I_cz', а вторая - массе тела М. Найдем значение третьей суммы. На основании фор­мул для координат центра масс .Так как в на­шем случае точка С является началом координат, то x_C = 0 и, сле­довательно, . Окончательно получаем:

Формула выражает следующую теорему Гюйгенса-Штейнера:

Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

 

Момент инерции тела относительно произвольной оси.

Найдем момент инерции тела относительно оси u, проходящей через некоторую точку О (рис. 7).

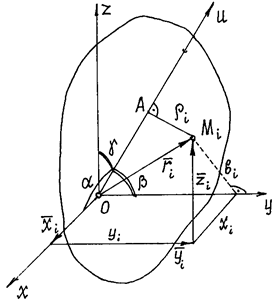
Рис.7

 

По определению момент инерции .

Поместим в точку О начало координатных осей x, y, z. Из прямоугольного треугольника ОАМ_i следует , где . И так как радиус-вектор точки : , то, проектируя это равенство на ось u, получим  (, , - углы между осью u и осями x, y, z).

Рис. 14.3.

Как известно из тригономет­рии .

Поэтому

И, группируя подобные члены, содержащие косинусы одинаковых углов, получим:

 

Но  

где  - расстояния от точки М_i до осей x, y, z, соответственно.

Поэтому

где I_x, I_y, I_z – моменты инерции тела относительно осей координат; I_xy, J_yz, J_xz  - центробежные моменты инерции относительно осей отмеченных в индексах.

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется главной осью инерции. Например, если J_yz = 0 и J_xz = 0, то ось z – главная ось инерции.

Так как все моменты инерции зависят от того, где находится точка О, от выбора начала координат, то обязательно надо указать для какой точки определены эти моменты инерции. Если начало координат взято в центре масс С, то все главные оси инерции называются главными центральными осями инерции.

Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (2) упрощается:

.                           (3)

Иногда по некоторым признакам нетрудно найти главные оси инерции тела.

1. Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.

Действительно. Направим координатную ось z по оси симметрии. Тогда для каждой точки тела с координатами (x_i, y_i, z_i) можно отыскать точку с координатами (-x_i, -y_i, -z_i) и поэтому центробежные моменты инерции  и . Значит ось z – главная ось инерции, и центральная ось, т.к. центр масс, как известно, находится на оси симметрии. Причём, эта ось будет главной для любой точки расположенной на оси симметрии.

2.  Если у однородного тела имеется плоскость симметрии, то любая ось перпендикулярная ей будет главной осью инерции для всех точек этой плоскости.

Направим ось z перпендикулярно плоскости симметрии из любой её точки О, назначив там начало координат. Тогда для каждой точки тела с координатами  (x_i, y_i, z_i) можно найти симметричную ей точку с координатами (x_i, y_i, - z_i). Поэтому центробежные моменты инерции I_xz и I_yz будут равны нулю. Значит ось z – главная ось инерции.

 

Уравнение динамики вращательного движения твердого тела.

Для того чтобы тело, закрепленное на оси, привести во вращение или изменить угловую скорость его вращения, к телу необходимо приложить силу . При вращении тела результат действия силы зависит не только от ее значения, но и от того, на каком расстоянии от оси вращения и под каким углом она приложена.

Моментом силы  относительно неподвижной оси вращения называется векторное произведение радиус-вектора  точки приложения силы на эту силу  (рис.9):

Вектор  направлен вдоль оси вращения в сторону, определяемую правилом правого винта (рис.10). Модуль момента силы определяется выражением:

где r∙sinα=h - плечо силы F; α – угол между  и .

 

Рис.9

 

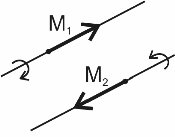
Рис. 10

 

Плечом силы h называют кратчайшее расстояние между линией действия силы и осью вращения (рис. 9). Таким образом, момент силы равен произведению силы на плечо этой силы:

M=F∙h  [Н∙м].

Уравнение динамики вращательного движения твердого тела имеет вид

Момент действующих на тело сил равен произведению момента инерции тела на угловое ускорение.                                                                                   

Дифференциальные уравнения движения системы.

Рас­смотрим систему, состоящую из п материальных точек. Выделим какую-нибудь точку системы с массой . Обозначим равнодейству­ющую всех приложенных к точке внешних сил (и активных и реак­ций связей) через , а равнодействующую всех внутренних сил – через . Еслиточка имеет при этом ускорение , то по основному закону динамики

.

Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

 

Эти уравнения, из которых можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме. Уравнения являются дифференциальными, так как ; входящие в правые части уравнений силы будут в общем случае зависеть от времени, координат точек системы и их скоростей.

Проектируя на какие-нибудь координатные оси, мы можем получить дифференциальные уравнения движения системы в проекциях на эти оси.

Полное решение основной задачи динамики для системы состояло бы в том, чтобы, зная заданные силы, проинтегрировать соответ­ствующие дифференциальные уравнения и определить таким путем закон движения каждой из точек системы в отдельности.

Однако такой путь решения обычно не применяется по двум причинам. Во-первых, этот путь слишком сложен и почти всегда связан с непреодолимыми математическими трудностями. Во-вторых, в большинстве случаев при решении задач механики бывает доста­точно знать некоторые суммарные характеристики движения системы в целом, а не движение каждой из ее точек в отдельности. Эти суммарные характеристики определяются с помощью общих теорем динамики системы, к изучению которых мы и перейдем.

Основная роль уравнений состоит в том, что они, или след­ствия из них, являются исходными для получения соответствующих общих теорем.

Общие теоремы динамики механической системы: теоремы о движении центра масс механической системы и об изменении количества движения, теоремы об изменении кинетического момента и кинетической энергии, являются следствием основного уравнения динамики. Данные теоремы рассматривают не движение отдельных точек и тел, входящих в механическую систему, а некоторые интегральные характеристики, такие как движение центра масс механической системы, ее количество движения, кинетический момент и кинетическую энергию. В результате из рассмотрения исключаются неизвестные внутренние силы, а в ряде случаев и реакции связей, что существенно упрощает решения задачи.

 

Теорема о движении центра масс.

В ряде случаев для определения характера движения системы (особенно твердого тела), достаточно знать закон движения ее центра масс. Например, если бросить камень в цель, совсем не нужно знать как он будет кувыркаться во время полета, важно установить попадет он в цель или нет. Для этого достаточно рассмотреть движение какой-нибудь точки этого тела.

Чтобы найти этот закон, обратимся к уравнениям движения системы и сложим по­членно их левые и правые части. Тогда получим:

Преобразуем левую часть равенства. Из формулы для радиус-вектора центра масс имеем:

Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме произ­водных, найдем:

или                 

где - ускорение центра масс системы. Так как по свойству вну­тренних сил системы , то, подставляя все найденные значения, получим окончательно:

Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая с уравнением дви­жения материальной точки, получаем другое вы­ражение теоремы: центр масс системы движется как мате­риальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

Проектируя обе части равенства  на координатные оси, получим:

Эти уравнения представляют собою дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.

Значение доказанной теоремы состоит в следующем.

1) Теорема дает обоснование методам динамики точки. Из урав­нений видно, что решения, которые мы получаем, рассмат­ривая данное тело как материальную точку, определяют закон движения центра масс этого тела, т.е. имеют вполне конкрет­ный смысл.

В частности, если тело движется поступательно, то его движе­ние полностью определяется движением центра масс. Таким образом, поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе тела. В остальных слу­чаях тело можно рассматривать как материальную точку лишь тогда, когда практически для определения положения тела достаточно знать положение его центра масс.

2) Теорема позволяет при определении закона движения центра масс любой системы исключать из рассмотрения все наперед неиз­вестные внутренние силы. В этом состоит ее практическая ценность.

Так движение автомобиля по горизонтальной плоскости может происходить только под действием внешних сил, сил трения, действующих на колеса со стороны дороги. И торможение автомобиля тоже возможно только этими силами, а не трением между тормозными колодками и тормозным барабаном. Если дорога гладкая, то как бы не затормаживали колеса, они будут скользить и не остановят автомобиль.

Или после взрыва летящего снаряда (под действием внутренних сил) части, осколки его, разлетятся так, что центр масс их будет двигаться по прежней траектории.

Теоремой о движении центра масс механической системы следует пользоваться для решения задач механики, в которых требуется:

            - по силам, приложенным к механической системе (чаще всего к твердому  телу), определить закон движения центра масс;

            - по заданному закону движения тел, входящих в механическую систему, найти реакции внешних связей;

            - по заданному взаимному движению тел, входящих в механическую систему, определить закон движения этих тел относительно некоторой неподвижной системы отсчета.

            С помощью этой теоремы можно составить одно из уравнений движения механической системы с несколькими степенями свободы.

            При решении задач часто используются следствия из теоремы о движении центра масс механической системы.

       Следствие 1. Если главный вектор внешних сил, приложенных к механической системе, равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно. Так как ускорение центра масс равно нулю, .

            Следствие 2.  Если проекция главного вектора внешних сил на какую-нибудь ось равна нулю, то центр масс системы или не изменяет своего положения относительно данной оси, или движется относительно нее равномерно.

Например, если на тело начнут  действовать две силы, образующие пару сил (рис.12), то центр масс С его будет двигаться по прежней траектории. А само тело будет вращаться вокруг центра масс. И неважно, где приложена пара сил.

Кстати, в статике мы доказывали, что действие пары на тело не зависит от того, где она приложена. Здесь мы показали, что вращение тела будет вокруг центральной оси С.

Рис.12

  

Теорема об изменении кинетического момента.

Кинетический момент механической системы  относительно неподвижного центра O является мерой движения системы вокруг этого центра. При решении задач обычно применятся не сам вектор , а его проекции на оси неподвижной системы координат, которые называются кинетическими моментами относительно оси. Например, K_z - кинетический момент системы относительно неподвижной оси Oz .

Кинетический момент механической системы складывается из кинетических моментов точек и тел, входящих в эту систему. Рассмотрим способы определения кинетического момента материальной точки и твердого тела при различных случаях их движения.

Для материальной точки с массой , имеющей скорость , кинетический  момент  относительно некоторой оси Oz определяется как момент вектора количества движения этой  точки  относительно выбранной оси:

Кинетический момент точки считается положительным, если со стороны положительного направления оси движение точки происходит против часовой стрелки.

Если точка совершает сложное движение, для определения ее кинетического момента следует вектор количества движения  рассматривать как сумму количеств относительного и переносного движений (рис.15)

Тогда

Но , где  - расстояние от точки до оси вращения, и

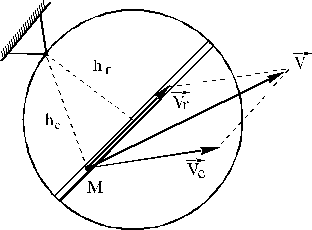
Рис. 15

 

Вторую составляющую вектора кинетического момента  можно определить так же, как и момент силы относительно оси. Как и для момента силы, величина  равна нулю, если вектор относительной скорости лежит в одной плоскости с осью переносного вращения.

Кинетический момент твердого тела относительно неподвижного центра можно определить как сумму двух составляющих: первая из них характеризует поступательную часть движения тела вместе с его центром масс, вторая - движение системы вокруг центра масс:

.

Если тело совершает поступательное движение, то вторая составляющая равна нулю

.

Наиболее просто вычисляется кинетической момент твердого тела при его вращении вокруг неподвижной оси

,

где  - момент инерции  тела  относительно  оси  вращения.

Теорема об изменении кинетического момента механической системы при ее движении вокруг неподвижного центра формулируется следующим образом: полная производная по времени от вектора кинетического момента механической системы относительно некоторого неподвижного центра O по величине и направлению равна главному моменту внешних сил, приложенных к механической системе, определенному относительно того же центра

где   - главный момент всех внешних сил относительно центра О.

При  решении  задач, в которых рассматриваются тела, вращающиеся вокруг неподвижной оси, используют теорему об  изменении кинетического момента относительно неподвижной оси

Как и для теоремы о движении центра масс, теорема  об изменении кинетического момента имеет  следствия.

Следствие 1.  Если главный момент всех внешних сил относительно некоторого неподвижного центра равен нулю, то кинетический момент механической   системы относительно этого центра остается неизменным.

Следствие 2.  Если главный момент всех внешних сил относительно некоторой неподвижной оси равен нулю, то кинетический момент механической системы относительно этой оси остается неизменным.

Теорема об изменении кинетического момента применяется для решения задач, в которых рассматривается движение механической системы, состоящей из центрального тела, вращающегося вокруг неподвижной оси, и одного или нескольких тел, движение которых связано с центральным.. Связь может осуществляться при помощи нитей, тела могут перемещаться по поверхности центрального тела или в его каналах за счет внутренних сил. С помощью  данной теоремы можно определить зависимость закона вращения центрального тела от положения или движения остальных тел.

 

 

Закон сохранения движения центра масс.

Из теоремы о движении центра масс можно получить следующие важные следствия:

1) Пусть сумма внешних сил, действующих на систему, равна нулю

.

Тогда из уравнения  следует, что  или . Следовательно, если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, т. е. равномерно и прямолинейно. В частности, если вначале центр масс был в покое, то он и останется в покое. Действие внутренних сил, как мы видим, движение центра масс системы изменить не может.

2) Пусть сумма внешних сил, действующих на систему, не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например, ось Ох) равна нулю:

.

Тогда уравнение  дает:   или .

Следовательно, если сумма проекций всех действующих внеш­них сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в начальный момент , то и в любой после­дующий момент , т.е. центр масс системы в этом случае вдоль оси Ох перемещаться не будет ().

Все эти результаты выражают собою закон сохранения движе­ния центра масс системы. Рассмотрим некоторые примеры, иллю­стрирующие его приложения.

а) Движение центра  масс солнечной системы. Так как притяжением звезд можно практически пренебречь, то можно считать, что на солнечную систему никакие внешние силы не дей­ствуют. Следовательно, в первом приближении ее центр масс дви­жется в мировом пространстве равномерно и прямолинейно.

б) Действие пары сил на тело. Если на свободное твердое тело начнет действовать пара сил , то геометрическая сумма этих внешних сил будет равна нулю . Следовательно, центр масс С тела, если он вначале был неподвижен, должен остаться неподвижным и при действии пары. Таким образом, где бы к свободному твердому телу ни была при­ложена пара сил, тело начнет вращаться вокруг своего центра масс.

в) Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий (силы внутренние) не мог бы двигаться вдоль горизонтальной пло­скости, так как в этом случае сумма проекций на любую горизон­тальную ось Ох всех приложенных к человеку внешних сил (сила тяжести и реакция плоскости) будет равна нулю и центр масс человека вдоль плоскости перемещаться не будет ().

Если, например, человек вынесет правую ногу вперед, то левая его нога скользнет назад, а общий центр масс останется на месте.

При наличии же трения скольжению левой ноги назад будет пре­пятствовать сила трения, которая в этом случае будет направ­лена вперед. Эта сила и будет той внешней силой, которая позволяет человеку перемещаться в сторону ее действия (в данном случае вперед).

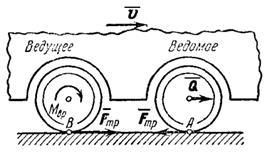
Рис.17

 

Аналогично происходит движение паровоза или автомобиля. Сила давления пара или газа в двигателе является силой внутренней и сама но себе не может переместить центр масс системы. Движение происхо­дит потому, что двигатель передает соответствующим колесам, назы­ваемыми ведущими, вращающий мо­мент. При этом точка касания В ве­дущего колеса (рис.13) стремится скользить влево. Тогда на колесо будет  действовать  сила  трения, направленная вправо. Эта внешняя сила и позволит центру тяжести паровоза или автомобиля дви­гаться вправо. Когда этой силы нет или когда она недостаточна для преодоления сопротивления, испытываемого ведомыми колесами, движения вправо не будет; ведущие колеса будут при этом вра­щаться на месте (буксовать).

5)

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю^[1].

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении системы в пустом пространстве импульс сохраняется во времени, а при наличии внешнего воздействия скорость изменения импульса определяется суммой приложенных сил.