3. Энергия электростатического поля

1. Энергия системы точечных зарядов как сумма энергия парного взаимодействия зарядов ( и принцип суперпозиции)

Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:

,

где W_п1 и W_п2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно

.

При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r₁ и r₂ от заряда Q,

.

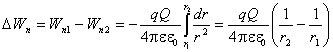Если поле создано системой точечных зарядов Q₁, Q₂,¼, Q_n, то изменение потенциальной энергии заряда q в этом поле:

.

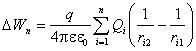Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим

,

где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид

.

При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:

.

Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q_i (i = 1, 2, ... ,n). Энергия взаимодействия всех n зарядов определится соотношением

 ,

где r_ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.

Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля, определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W_п / q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).

Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :

.

Принцип суперпозиции. Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q_1, Q₂¼, Q_n имеем

 ,

где r_i - расстояние от точки поля, обладающей потенциалом j, до заряда Q_i. Если заряд произвольным образом распределен в пространстве, то

 ,

где r - расстояние от элементарного объема dx, dy, dz до точки (x, y, z), где определяется потенциал; V - объем пространства, в котором распределен заряд.

Потенциал и работа сил электрического поля. Основываясь на определении потенциала, можно показать, что работа сил электрического поля при перемещении точечного заряда q из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов в начальной и конечной точках пути, A = q (j₁ - j₂). Если по аналогии с потенциальной энергией считать, что в точках, бесконечно удалённых от электрических зарядов - источников поля, потенциал равен нулю, то работу сил электрического поля при перемещении заряда q из точки 1 в бесконечность можно представить как A_¥ = q j₁. Таким образом, потенциал â данной точке электростатического поля - этофизическая величина, численно равная работе, совершаемой силами электрического поля при перемещении единичного положительного точечного заряда из данной точки поля в бесконечно удаленную: j = A_¥ / q. В некоторых случаях потенциал электрического поля нагляднее определяется какфизическая величина, численно равная работе внешних сил против сил электрического поля при перемещении единичного положительного точечного заряда из бесконечности в данную точку. Последнее определение удобно записать следующим образом:

 .

В современной науке и технике, особенно при описании явлений, происходящих в микромире, часто используется единица работы и энергии, называемая электрон-вольтом (эВ). Это работа, совершаемая при перемещении заряда, равного заряду электрона, между двумя точками с разностью потенциалов 1 В: 1 эВ = 1,60×10^-19 Кл×1 В = 1,60×10^-19 Дж.

2. Интегральное представление энергии непрерывного распределения зарядов, cравнение со случаем энергии системы точечных зарядов

Пусть в элементе объема находится заряд. Для определения энергии взаимодействия всех элементовв объеме V можно использовать формулу(12.4). , перейдя в ней от суммы к интегралу:

 (12.5)

Где - потенциал, создаваемый всеми зарядами в точке нахождения заряда.

На первый заряд формулы (12.4) и (12.5) кажутся аналогичными, тем более что (12.5) “выведена” из (12.4). Однако между ними существует принципиальное различие. Формула (12.4) учитывает лишь энергию взаимодействия между заряженными шарами, но не учитывает энергию взаимодействия между элементами зарядов, находящихся на каждом шаре. А (12.5) учитывает и первое, и второе.

Учитывая сказанное, энергию взаимодействия зарядов можно записать в виде:

 (12.6)

Величина - это энергия заряженных шаров, учитывающая взаимодействие зарядов между собой на каждом шаре. Собственная энергия зависит от законов распределения зарядов шара и значений зарядов. Если имеется уединенный шар, то.

Тогда (12.7)

Это означает, что собственная энергия точечного заряда равна бесконечности.

Но при . Это приводит к серьезным трудностям при использовании модели точечных зарядов.

3. Электрическая энергия заряженных уединенного проводника и конденсатора

Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен , а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная. Но потенциал электростатического поля данного проводника в бесконечности равен нулю. Тогда

При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.

Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:

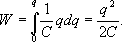
Применяя соотношение , можно получить следующие выражения для потенциальной энергии W:

(16.2)

Для заряженного конденсатора разность потенциалов (напряжение) равна поэтому соотношение для полной энергии его электростатического поля имеют вид

4. Энергия электростатического поля, выраженная в виде объемного интеграла от векторов напряжённости Е и электрического смещения D.

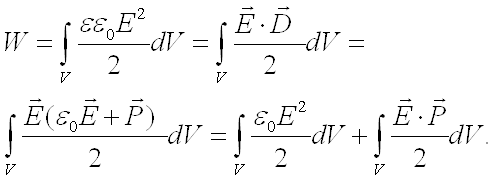
5. Выражение силы, действующей на проводник, погруженный в жидкий или газообразный диэлектрик, через объемную плотность энергии электрического поля вблизи проводника.

При наличии среды вычисление сил, действующих на проводники и диэлектрики, усложняется.

Прежде всего выражение для объемной силыстановится несправедливым, даже если под понимать молекулярную плотность заряда. Это связано с тем, чтоесть средняя макроскопическая плотность, которая не учитывает поляризацию отдельных молекул. Между тем в неоднородном электрическом поле на поляризованную молекулу действует сила. Можно было бы попробовать усреднить эту силу по объему, но такая процедура наталкивается на значительные трудности. Воспользуемся энергетическим методом вычисления сил.

Рассмотрим несколько типичных задач. Найдем силу, действующую на диэлектрический шар, помещенный в слабо неоднородное поле. Последнее условие означает, что поле должно мало меняться на размере шара. Тогда дипольный момент шара будет приблизительно такой же, как и в однородном поле: где Е — внешнее поле (в отсутствие шара). Так как момент шара пропорционален полю, от он ведет себя как квазиупругий диполь и, следовательно, его энергия в поле . Произведем теперь виртуальное перемещение шара во внешнем неоднородном поле и запишем баланс энергии: где — сила, действующая на шар со стороны поля:

(19.1)

т. е. диэлектрик втягивается в сильное поле. Если (слабый диэлектрик), то выражение (19.1) справедливо для диэлектрика произвольной формы, так как в этом случае можно пренебречь взаимодействием отдельных участков диэлектрика, которые поляризуются независимо друг друга. Тогда объемная сила, действующая на диэлектрик,

(19.2)

т. е. определяется изменением плотности энергии электрического поля при внесении диэлектрика.

Кроме силы, действующей в неоднородном электрическом поле на диэлектрик как целое, в нем возникают еще и внутренние напряжения, называемые стрикционными силами. Рассмотрим пластину диэлектрика, помещенную в плоский конденсатор (рис. 11.5). Ясно, что под действием стрикционных сил пластина несколько

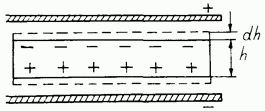
Рис. 11.5. К расчету стрикционных сил.

растянется вдоль поля. Попробуем вычислить стрикционные силы в этом примере. Воспользуемся энергетическим методом. При небольшем растяжении пластины изменение энергии поля складывается из двух частей. Во-первых, в слое энергия поля в вакууме заменяется на энергию поля в среде Здесь поле в вакуумном зазоре, которое не изменяется при деформации диэлектрика, поскольку мы принимаем заряд на конденсаторе неизменным (см. выше). Во-вторых, необходимо учесть изменение энергии во всем объеме вещества из-за изменения его плотности, от которой зависит диэлектрическая проницаемость: где .Частная производная взята здесь при постоянной температуре, чтобы исключить зависимость от температуры. Полный баланс энергии на единицу площади диэлектрика имеет вид

(19.3)

Отсюда натяжение, действующее на диэлектрик,

(19.4)

можно рассматривать как разность натяжений снаружи и изнутри диэлектрика, где Е —электрическое поле внутри последнего.

Обычно стрикционным давлением называется величина

(19.5)

Это давление не дает вклада в силу, действующую на диэлектрик как целое, при условии, что он окружен вакуумом.

Рассмотрим, наконец, произвольную систему заряженных тел, погруженных в однородный жидкий диэлектрик. Как мы уже знаем , такая среда ослабляет поле в раз, не изменяя его конфигурации. Отсюда, в частности, следует, что энергия поля также в раз меньше, чем в вакууме. Значит, и работа по перемещению зарядов, и силы между телами тоже уменьшаются в раз. На первый взгляд этот вывод кажется тривиальным: раз поле уменьшается в раз, то во столько же раз должна уменьшиться и сила его воздействия на заряд. Однако под полем в среде понимается среднее поле, тогда как действующее на заряд локальное поле зависит от формы полости, т. е. от формы заряженного тела. Чтобы разобраться, в чем здесь дело, вернемся к предыдущему примеру. Пусть диэлектрик является теперь жидким и заполняет весь конденсатор. Тем не менее мы можем представить себе, что между диэлектриком и пластиной конденсатора существует очень

тонкая щель, в которой поле равно так что все предыдущее рассмотрение остается в силе. В таком случае давление поля непосредственно на пластину равно т. е. такое же, как в вакууме, вместо ожидаемого ослабления в раз. Этот пример подтверждает, что сила, действующая со стороны поля на заряженное тело, действительно зависит от формы тела.

Однако жидкий диэлектрик имеет, как правило, механический контакт с телом и тоже действует на него с некоторой силой, которая в рассматриваемом примере дается выражением (19.4). Наконец, нужно учесть еще дополнительное давление в жидкости, возникающее за счет электрического поля и равное стрикционному давлению (19.5). Таким образом, полное давление на пластину

(19.6)

в соответствии с энергетическими соображениями.

Подчеркнем еще раз, что такой простой результат получается только для жидкого однородного диэлектрика. Механический контакт проводников с твердым диэлектриком является, как правило, неопределенным. Кроме того, внутренние упругие напряжения зависят теперь не от локального стрикционного давления, а от сил, действующих на весь диэлектрик.