- •§1.Общая характеристика атомов.
- •§2.Законы теплового излучения.
- •§3.Испускание и поглощение излучения по квантовой теории. Вывод формулы Планка по Энштейну., 1916г.
- •§5. Ядерная модель атома. Формула резерфорда.
- •§14. Дифракция рентгеновских лучей (рл) на кристаллической решетке.
- •§15. Формула Вульфа-Брегга.
- •§16. Экспериментальное наблюдение дифракции
- •§17. Корпускулярно волновой дуализм.
- •§18. Эффект Комптона.
- •§19. Волновые свойства частиц.
- •§20. Экспериментальное подтверждение гипотезы де Бройля.
- •§21. Статистическая интерпретация волн де Бройля.
- •§22. Соотношение неопределенностей Гейзенберга 1927г.
- •§23. Постулаты квантовой физики.
- •§24. Принцип суперпозиции квантовых состояний.
- •§25. Примеры движения квантовой частицы в стационарных
- •§26. Момент импульса квантовой теории.
- •§27. Гипотеза Уленбека (Юленбека) и Гаудсмита о спине электрона.
- •§28. Спектр атома водорода.
- •§29. Щелочные металлы.
- •§36. Эффект Зеемана.
- •§37. Неразличимость тождественных квантовых частиц.
- •§ 38. Периодическая система элементов (псэ)
§22. Соотношение неопределенностей Гейзенберга 1927г.
Волновые
свойства микрочастиц нельзя понять,
если представлять их материальными
точками, движущимися по определенным
траекториям. Кроме того, характеризовать
микрочастицу классическими величинами,
такими, как
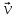 ,
, ,
,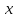 …
также нельзя, т.к., строго говоря, эти
величины микрочастице не свойственны.
…
также нельзя, т.к., строго говоря, эти
величины микрочастице не свойственны.
Описание
микрочастицы в квантовой физике
выполняется с помощью волновой функции
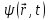 ,
степень применимости классических
понятий для характеристики микрочастиц
определяется соотношениями неопределенности
Гейзенберга, которые являются
математической формулировкой
универсального закона природы,
корпускулярно-волнового дуализма.
,
степень применимости классических
понятий для характеристики микрочастиц
определяется соотношениями неопределенности
Гейзенберга, которые являются
математической формулировкой
универсального закона природы,
корпускулярно-волнового дуализма.
Неопределенность координаты:
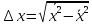
Неопределенность компоненты импульса:
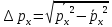
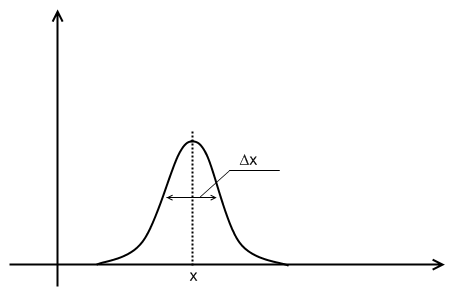

Никаких ограничений на перекрестные произведения нет.
Т.о., если мы абсолютно точно знаем координату, то ее неопределенность стремится к нулю, следовательно мы ничего не знаем про импульс.
Рассмотрим дифракцию электронов на щели.
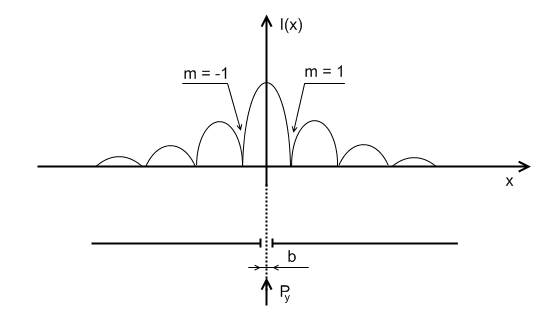
До
прохождения щели мы точно знаем импульс
электрона
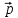 и, соответственно, ничего не знаем про
координату. При прохождении щели
неопределенность становится порядка
размера щели, значит:
и, соответственно, ничего не знаем про
координату. При прохождении щели
неопределенность становится порядка
размера щели, значит:
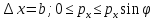
Рассмотрим
центральный максимум, ограниченный
минимумами порядка

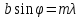

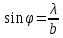
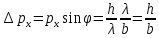
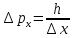

Чем больше масса частицы, тем точнее возможно совместное измерение координаты и скорости.
Классическое определение скорости:
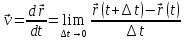
Уравнение траекторий:

В силу соотношений неопределенности, понятие траекторий для микрочастицы теряет смысл.
Рассмотрим пример шарика, наблюдаемого в микроскоп.

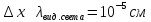

Как видим, ошибка скорости не значительна, в опыте не регистрируется, а значит можно считать, что шарик движется по некоторой траектории.
Рассмотрим пример электрона в атоме.
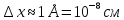

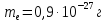
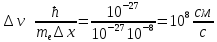
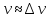
Следовательно, мы ничего не знаем о скорости электрона и не можем говорить о какой-либо траектории или орбите.
Рассмотрим
пример движения электронов, ускоренных
разностью потенциалов
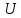 вдоль одной оси со скоростью
вдоль одной оси со скоростью .
.
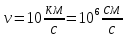
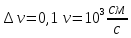
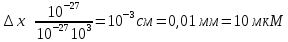
В данном случае можно говорить о траектории электрона.
Оценим с помощью соотношений неопределенности линейные размеры атома водорода и его минимальную энергию.
Если бы электрон упал на ядро, то мы бы точно знали его координату и импульс, но это запрещено соотношениями Гейзенберга.
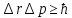
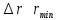
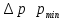


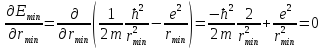

 -
не имеет смысла, т.к. атома, в таком
случае, не существует.
-
не имеет смысла, т.к. атома, в таком
случае, не существует.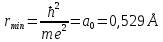

Выводы:
Согласно квантовой механике, существует принципиальный предел точности измерений, который лежит в основе природы и не может быть превзойден никакими улучшениями условий эксперимента.
Понятие траекторий для пространственного движения микрочастиц теряет смысл.
Для микрочастиц теряет смысл разделение энергии на кинетическую и потенциальную.
Классический момент импульса в квантовой механике также теряет смысл.
Квантовая микрочастица никогда не бывает в состоянии покоя.
Кроме соотношений неопределенности для координаты и импульса, известны соотношения и для всех других сопряженных пар физических величин, в частности, для энергии и времени:
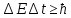
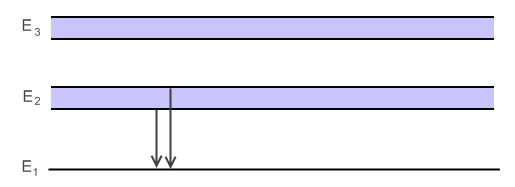
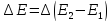
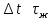
Любой возбуждаемый уровень уширен, а значит уширена и спектральная линия:

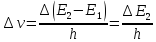

§23. Постулаты квантовой физики.
Уравнение Шредингера 1925г.
Движению частицы сопоставляется волновая функция
Волновая функция подчиняется уравнению Шредингера
Любой физической величине сопоставляется линейный самосопряженный оператор
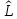 , собственные значения которого
вещественны
, собственные значения которого
вещественныПринцип суперпозиции квантовых состояний
Тождественные квантовые частицы принципиально не различимы, для них выполняется принцип Паули
Уравнение Шредингера:

Нестационарное или временное уравнение Шредингера для релятивистской частицы без спина.
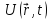 -
потенциальная функция, если она не
зависит явно от времени
-
потенциальная функция, если она не
зависит явно от времени
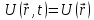 , то она имеет смысл потенциальной
энергии в данной точке пространства.
, то она имеет смысл потенциальной
энергии в данной точке пространства.
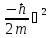 -
оператор
кинетической энергии.
-
оператор
кинетической энергии.
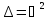 -
оператор Лапласса
-
оператор Лапласса
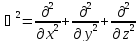
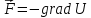
Зная потенциал, всегда можно найти силу.
Будем
считать, что потенциал
 зависит только от координаты и решение
уравнения будем искать в виде стационарных
волновых уравнений:
зависит только от координаты и решение
уравнения будем искать в виде стационарных
волновых уравнений:
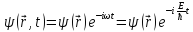
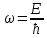
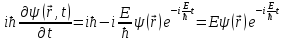

Стационарное уравнение Шредингера (СУШ):
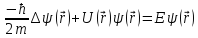
Вероятность
обнаружения частицы в объеме
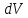 окрестности точки
окрестности точки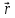 в момент времени
в момент времени :
:
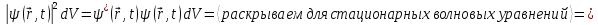

Для стационарных волновых функций вероятность не зависит от времени.
Математические требования к волновой функции:
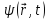 должна
быть непрерывна, конечна и однозначна
должна
быть непрерывна, конечна и однозначна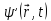 должна
быть непрерывна и конечна
должна
быть непрерывна и конечнаВ области, где потенциальная энергия
 ,
частица находится не может, значит
волновая функция в этой области
,
частица находится не может, значит
волновая функция в этой области ,
из условия непрерывности следует, что
волновая функция
,
из условия непрерывности следует, что
волновая функция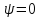 и на границе с этой областью.
и на границе с этой областью.
В квантовой механике всем динамическим переменным сопоставляются линейные операторы, например, в координатном представлении оператором координаты умножается на координату:
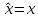
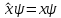
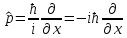

Оператор
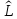 называют Эрмитовым или сопряженным,
если выполняется следующее условие:
называют Эрмитовым или сопряженным,
если выполняется следующее условие:
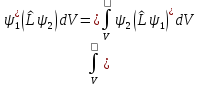
Собственные значения таких операторов действительные.
СУШ в операторной форме:
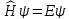
Уравнение на собственные функции и собственные значения Гамильтона:

Решая
УШ, получаем набор значений энергии
 , которым соответствуют функции
, которым соответствуют функции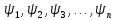
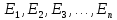 -
собственные значения или энергитический
спектр Гамильтониана.
-
собственные значения или энергитический
спектр Гамильтониана.
Т.о. квантование энергии автоматически вытекает из вида УШ без каких-либо дополнительных условий.
Например, правило квантования Бора:
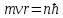
Спектр Гамильтониана может быть дискретным (соответствует финитному движению), либо непрерывным (инфинитному движению), или смешанным.
Вид
спектра зависит от вида конкретного
оператора
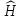 .
Допустим, найдены все собственные
значения энергий и они дискретны, пусть,
также, эти значения невырождены (каждому
конкретному состоянию соответствует
свое, отличное от других, значение
энергии):
.
Допустим, найдены все собственные
значения энергий и они дискретны, пусть,
также, эти значения невырождены (каждому
конкретному состоянию соответствует
свое, отличное от других, значение
энергии):
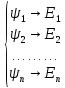
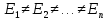
В
этом случае, набор волновых функций
 образует полную или базисную систему
функций, и все они ортогональны друг
другу.
образует полную или базисную систему
функций, и все они ортогональны друг
другу.
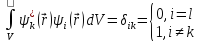
Условие нормировки: