Тимофеева, УМК, Математика для гуманитариев

16.Классификация – представление множества в виде объединения непустых попарно не пересекающихся подмножеств.

Тренировочные задания по теме 2.1.

1.L – множество букв, из которых состоит слово «анаконда». Какова численность элементов множества L?

2.H – множество букв, из которых состоит слово «канон». Сравните численности множаеств H и множества L (из предыдущего задания).

3. Всегда ли выполняется соотношение |A B| = |A| + |B| ?

4.Всегда ли выполняется соотношение |A\B| = |A| - |B| ?

5.Из каких элементов состоят следующие множества А и В? А={x x – животное} {x x - хищник}

В={x x – животное} {x x - хищник}

6.А – множество всех белок, бегающих по Академгородку в данный момент времени; В – множество млекопитающих, населяющих Землю в данный момент времени. Каковы элементы множества А\В?

7.А – множество людей, присутствующих сейчас в данной аудитории, В – множество студентов Оксфордского университета. Каковы элементы множества А\В?

8.Группа, состоящая из 20 человек, отправилась в туристическую поездку. Из них 14 человек знают английский язык, 5 – итальянский, один человек знает оба языка. Сколько человек не знает ни английского, ни итальянского? Какие операции над множествами вы использовали для ответа на вопрос?

9.Вспомните какие-либо произведения (проза, стихи, кинофильмы и т.д.), название которых именует некоторое множество или операцию над множествами. Например, «Трое в лодке, не считая собаки»: А – люди, В – собаки, С – находящиеся в лодке,

(А В) С – люди и собаки, находящиеся в лодке; С \ В = 3.

10.Лингвист анализировал текст, состоящий из 100 предложений. В каждом предложении было хотя бы одно из местоимений «я» или «ты». Всего в тексте встретилось 60 местоимений «я» и 50 «ты». Известно, что ни в одном предложении ни одно из этих местоимений не встречается более одного раза. Сколько предложений содержат и то, и другое местоимение? Сколько предложений содержат «я», но не содержат «ты»? Какие операции над множествами вы использовали для ответа на вопрос?

11.Анаграмма – это перестановка букв или звуков определѐнного слова (или словосочетания), дающая в результате другое слово или словосочетание. Например, вертикаль – кильватер, апельсин – спаниель, старорежимность – нерасторжимость, австралопитек – ватерполистка, покраснение – пенсионерка, равновесие – своенравие, стационар – соратница, обезьянство – светобоязнь, антиквар – травинка, истопник – синоптик. Можно ли, воспользовавшись понятием «множество», точно определить, что такое «анаграмма»?

12.Пусть U – множество всех студентов нашего университета, α – свойство «быть студентом 2-го курса», β – свойство «быть спортсменом», А – множество всех студентов 2-го курса, В – множество всех спортсменов. Каковы элементы множеств А и В ? Какую классификацию множества U задают свойства α, β (см. рисунок)?

13.Как записать следующие соотношения: «Объект d не является элементом множества, являющегося пересечением множеств А и В», «Дополнение множества А до универсального множества U является собственным подмножеством объединения

Ви С»?

14.Какие из следующих соотношений верны?

с{а,в,с}

d {а,в,с} {а,в,с} {а,в,с} {а,в,с} {а,в,с} {а,в} {а,в,с}

с {в,{с}} {с} {в,{с}}

Тема 2.2. Отношения и функции

Упорядоченный набор элементов. Декартово произведение множеств. Понятие бинарного отношения, свойства бинарных отношений. Отношения эквивалентности, толерантности, строгого и нестрогого порядка. Понятие функции. Матрицы. Матричный способ изображение бинарного отношения. Понятия графа, виды графов. Некоторые проблемы теории графов. Изображение бинарного отношения с помощью графа.

Словарь терминов и обозначений по Теме 2.2

1.Упорядоченный набор, состоящий из N элементов, обозначается так: а1,а2,...,аN , а,в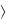– упорядоченная пара элементов. Если а в, то а,в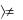в,а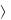

2.Пусть М, Q – некоторые множества; D - множество, состоящее из всевозможных упорядоченных пар х,у , где х – любой элемент из М, у – любой элемент из Q. Множество D, определѐнное таким образом, называют декартовым произведением множеств М, Q и обозначают D=М Q.

3.Декартовым произведением множеств М1, М2,…, МN называется множество DN, состоящее из всевозможных упорядоченных наборов вида х1,х2,…,хN , где х1 М1,

х2 М2,…, хN МN. Обозначение: DN=М1 М2 М3 … МN.

4.Бинарным (двухместным) отношением между элементами множеств М и Q на-

зывается любое подмножество R множества D=М Q. Вместо х,у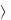 R можно писать хRу. Если х,у 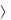R, то говорят, что соотношение хRу не выполнено. Например, отношение именования R можно определить так: М – множество имѐн, Q – множество людей, хRу тогда и только тогда, когда х,у М Q и х является именем для у.

5.Если М=Q, то R называется бинарным отношением на множестве М. Например,

отношение родства Р можно определить так: М – множество людей, хРу выполнено тогда и только тогда, когда х,у М М и человек х состоит в родстве с человеком у.

6.Некоторые из возможных свойств отношений:

a. Рефлексивность. Если для любого х М выполняется хRх, то отношение R рефлексивно. Например, отношения «равно», «одновременно» рефлексивны.

b.Антирефлексивность. Если для любых х,у М из соотношения хRу следует, что х у, то отношение R антирефлексивно Например, отношения «больше», «меньше» антирефлексивны.

c.Симметричность. Если для любых х,у М из соотношения хRу следует, что уRх, то отношение R симметрично. Например, отношения «родственник», «сосед» симметричны.

d.Антисимметричность. Если для любых х,у М из соотношений х у и хRу следует, что уRх не выполнено, то отношение R антисимметрично. Например, отношения «больше или равно», «меньше или равно» антисимметричны.

e.Асимметричность. Если для любых х,у М хотя бы одно из соотношений хRу или уRх не выполнено, то отношение R асимметрично. Например, отношения «больше», «меньше» асимметричны. Асимметричное отношение всегда антирефлексивно.

f.Транзитивность. Если для любых х,у М из соотношений хRу и уRz, всегда следует соотношение хRz, то отношение R транзитивно. Например, отношения «больше», «меньше», «больше или равно», «меньше или равно» транзитивны.

g.Антитранзитивность. Если для любых х,у М из соотношений хRу и уRz, всегда следует, что хRz не выполнено, то отношение R антитранзитивною Например, отношение «на единицу больше» антитранзитивно.

h.Если отношение R рефлексивно, симметрично, транзитивно, то оно называется эквивалентностью. Эквивалентность есть отношение одинаковости объектов (с определѐнной точки зрения). Например, в системе муниципальных корон, принятой Геральдическим Советом при Президенте РФ в 2005 г. (см. таблицу), отношение «х и у являются гербами одного и того же типа населѐнного пункта», заданное на множестве всех гербов Российской Федерации, есть эквивалентность.

i.Отношение R называется толерантностью, если оно рефлексивно и симметрично. Толерантность есть отношение сходства или смежности объектов (с определѐнной точки зрения). Например, на приведѐнном ниже рисунке День и ночь Мориса Корнелиуса Эшера каждая белая птица похожа на соседнюю с ней, но не тождественна ей, поэтому при продвижении взгляда влево можно заметить, что белые птицы постепенно превращаются лишь в фон для птиц серого цвета.

7.Отношение R называется отношением строгого порядка, если оно асимметрично, антирефлексивно и транзитивно. Например, отношения «больше», «меньше». Отношение «х является сыном у-а», заданное на множестве потомков Вильгельма I Завоевателя (см. приведѐнное ниже генеалогическое древо английских королей), есть отношение строгого порядка.

8.Отношение R называется отношением нестрогого порядка, если оно антисимметрично, рефлексивно и транзитивно. Например, отношения «больше или равно», «меньше или равно».

9.Пусть R – некоторое бинарное отношение. Отношение S называется обратным отношением, если хRу выполнено тогда и только тогда, когда выполнено уSх. Пример: конверсия (отношение «читать» является обратным к отношению «быть читаемым»).

10.Функция f есть бинарное отношение, заданное на множестве X Y) (т.е. множество упорядоченных пар <x,y> X Y), такое, что для любого x X существует единственный элемент y Y такой, что <x,y> f . Пример такого отношения приведѐн на следующем рисунке. Множество X называется областью определения функции f , а множество Y – областью значений функции f . Обозначение: f(x)=y. Переменную х называют независимой переменной (или аргументом), переменную y – зависимой переменной.

Y

X

11.Два множества А и В, на первом из которых задано отношение R, а на втором – S называются изоморфными, если существует взаимно-однозначная функция f с областью определения А и областью значений В, сохраняющая данное отношение, то есть (1) для любых х,у А, связанных отношением R, соответствующие им элементы из В связаны отношением S, и наоборот: (2) для любых g,h В, связанных отношением S, соответствующие им элементы из А связаны отношением R. Например, местность и карта этой местности, на которых заданы отношения «река х вдвое длиннее реки y» или «город х в два раза ближе к морскому побережью, чем город y» изоморфны.

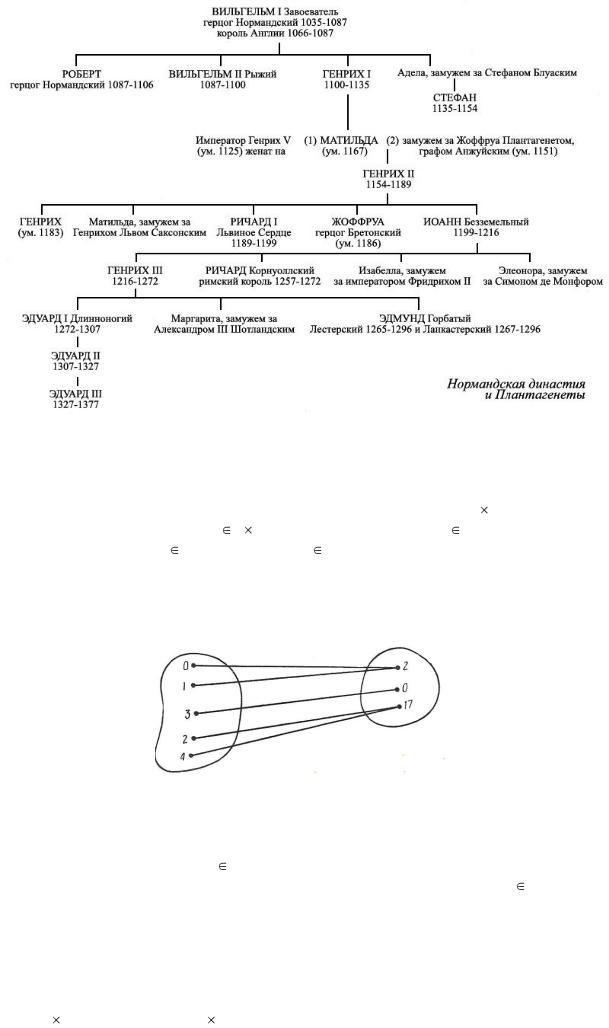
12.Матрица – прямоугольная таблица, составленная из элементов некоторого множества. Если матрица имеет m строк и n столбцов, то говорят, что она имеет размеры m n. Матрица размера n n называется квадратной.

13.Матричный способ задания бинарного отношения. Пусть М – множество мощ-

ности n, R – заданное на М бинарное отношение. Перенумеруем элементы М посредством целых чисел от 1 до n. Построим квадратную таблицу с n строками и n столбцами. Пусть х,у М и х – элемент с номером i, у – элемент с номером j. Построим матрицу, задающую отношение R. На пересечении i-й строки и j-го столбца поставим 1, если соотношение хRу выполнено, и 0, если соотношение хRу не выполнено. i-ая строка и i-ый столбец будут характеризовать i-й элемент множества М. Например, матрица для множества из четырѐх элементов будет иметь такой вид:

14.Задание бинарного отношения в виде графа. Пусть М – конечное множество.

Изобразим элементы множества М в виде точек плоскости. Если х,у М, х у и хRу, то проведѐм стрелку от х к у. Если х М и хRx, то нарисуем петлю, выходящую из х

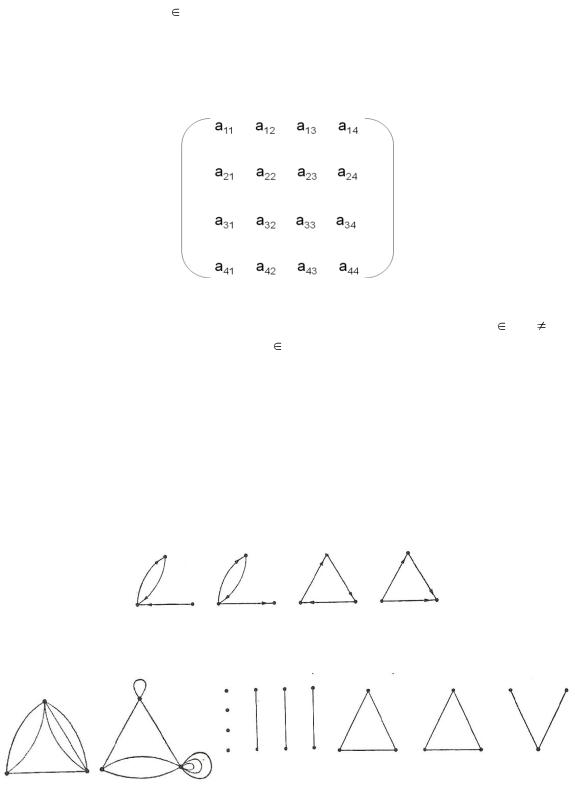
ивходящую в ту же точку. Если отношение симметрично (для любых х,у выполняются отношения хRу и уRх), то иногда удобнее вместо стрелок использовать линии. Такой граф называется неориентированным. В неориентированном графе линии, соединяющие вершины, называют рѐбрами. Граф, соответствующий несимметричному отношению (в котором вершины соединены стрелками) называют ориентированным, а стрелки, соединяющие вершины – дугами. Графы с пометками при вершинах называют помеченными графами. Ниже приведены примеры различных видов графов.

a.Ориентированные графы с тремя вершинами:

b.Неориентированные графы с тремя вершинами:

c. Неориентированные графы с четырьмя вершинами:

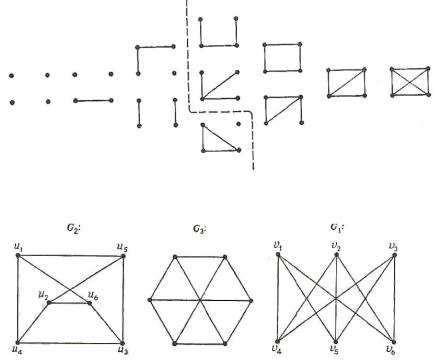
d. Помеченные и непомеченные графы:

15.Путь от вершины х к вершине у - это такая последовательность рѐбер, по которой можно перейти от х к у. При этом никакое ребро маршрута не встречается более одного раза. Вершина х называется начальной вершиной пути, вершина у — конечной вершиной. Количество рѐбер, составляющих путь, называют расстоянием между вершинами х и у

16.Две вершины графа называются связными, если в графе существует путь, в котором одна из этих вершин является начальной, а другая – конечной. Если такого пути не существует, вершины называются не связаннными.

17.Граф называется связным, если любая пара его вершин — связная. Граф называется несвязным, если в нем есть хотя бы одна несвязная пара вершин.

18.Цикл - путь, в котором начальная вершина совпадает с конечной.

19.Деревом называется любой связный граф, не имеющий циклов. Дерево может быть

ориентированным или неориентированным.

20.Вершина ориентированного дерева, в которую не входит ни одна дуга, называется корнем дерева. Вершины ориентированного дерева, у которых нет выходящих дуг, называются висячими (или терминальными) вершинами или листьями. Ниже приведены примеры различных видов деревьев.

21.Гипотеза четырѐх красок. Если имеется карта с изображением нескольких стран, то интересно узнать, сколько понадобится цветов для такой раскраски этих стран, чтобы никакие две соседние страны не были окрашены в один и тот же цвет. Согласно гипотезе о четырѐх красках предполагается, что любую карту на плоскости или поверхности шара можно раскрасить только четырьмя красками таким образом, чтобы никакие две смежные страны не были одного и того же цвета. Каждая страна должна состоять из одной связной области, а смежными называются страны, которые имеют общую границу в виде линии (а не просто одной общей точки).

Тренировочные задания по теме 2.2.

1.Допустим, что А – множество всех названий городов, В – множество всех стран, S

– бинарное отношение «находиться в». Приведите примеры элементов из множест-

ва D=А В?

2. Как будет соотноситься с множеством D (из предыдущего задания) множество, состоящее из всех упорядоченных пар х,у , где х А, у В, хSу?

3. Пусть W1, W2, W3, W4, W5 – соответственно множества слов русского, английского, французского, польского, татарского языков. W=W1 W2 W3 W4 W5 – декартово произведение заданных множеств. Построен словарь, ставящий в соответствие каждому слову русского языка один из возможных переводов этого слова на каждый из остальных перечисленных языков. Как с помощью введѐнных ранее понятий описать состав этого словаря? Можно ли сказать, что построенный словарь – это 5- местное отношение М W, состоящее из всех таких наборов х1,х2,х3,х4,х5 , где хi Wi, i {1,2,3,4,5} и каждое из слов х2-х5 является переводом слова х1 на соответствующий язык?

4.Допустим, что на множестве М задано некоторое бинарное отношение R, R М М. Какими свойствами может обладать данное отношение?

5.Какими свойствами обладают следующие отношения?

R1: x является столицей страны y

R2: x находится на территории y

R3: x является частью y

R4: x является студентом ВУЗа y

R5: x является преподавателем y

R6: слово x можно составить из букв слова y

R7: человек x такого же роста, как и человек y

6.Какие из следующих отношений являются функциями? Укажите области определения и области значений этих функций.

f(x) – отец х, f(x) – сын х,

f(x) – дедушка х,

f(x) – дедушка х со стороны матери, f(x) – старшая дочь х

7.Рассмотрим два варианта одной и той же мелодии, второй из которых получился в результате переноса первоначальной мелодии на октаву выше. Какой изоморфизм можно задать на множествах нот, составляющих эти две мелодии?

8.Определим множество М={Россия, США, Франция, Англия}. Перенумеруем эти

элементы в том порядке, в каком они здесь записаны. Рассмотрим отношения R1, R2 и изобразим эти отношения посредством матриц:

хR1у: х больше у по площади,

хR2у: х больше у по численности населения,

9.Пятеро молодых людей при встрече обменялись рукопожатиями (каждый с каждым пожали друг другу руки один раз). Сколько всего рукопожатий было сделано? Пусть S - отношение «обменяться рукопожатиями». Какими свойствами это отношение обладает?

10.Ниже приведѐно древо индоевропейской семьи языков. Какие отношения между языками можно задать на основе информации, представленной на этом древе? Укажите свойства введѐнных отношений.

11.Есть ли среди изображѐнных ниже графов одинаковые?

12.Задача о Кѐнигсбергских мостах: можно ли обойти все семь мостов города Кенигсберга (ныне Калининграда) таким образом, чтобы по каждому мосту пройти в точности один раз. Задача была поставлена и решена Эйлером в 1736 г. На приведѐнном ниже рисунке изображена схема расположения мостов в Кенигсберге.