
Тимофеева, УМК, Математика для гуманитариев
.pdf
Значит, некоторые s есть p.
Этот вывод правилен для любых предложений с данной логической структурой.
3.Задача логики – исследовать, какие операции над высказываниями позволяют сохранить истинность, то есть получить из истинных высказываний истинные высказывания. Для того чтобы точно и ясно описывать условия истинности высказываний вводятся специальные системы обозначений (логические языки).
4.Глубина логического анализа высказываний зависит от того, какой логический язык для этого используется. В рамках классической логики возможны два варианта.
a.Пропозициональная логика (или логика высказываний, или сентенцио-
нальная логика) используется для анализа логической структуры рассуждения в терминах простых высказываний, составляющих данное рассуждение, и логических связей между этими высказываниями. Внутреннее устройство простых высказываний при этом не учитывается (каждое из них рассматривается как неделимое целое).
b.Предикатная логика используется для более глубокого анализа рассуждения, учитывающего не только логические связи между составляющими его простыми высказываниями, но и внутреннее устройство этих простых высказываний.
5.Пропозиция (высказывание) – одно из базовых понятий языка пропозициональной логики. Пропозиция – то состояние дел в мире, о котором говорится в предложении. В классической (двузначной) логике пропозиция может принимать только одно из двух значений: «истина» или «ложь».
В повседневном языке существуют специальные средства для указания на пропозиции. Например, следующие предложения указывают на пропозицию р:
Мне сказали, что p |
Я знаю, что p |
Они полагают, что p |
Известно, что p |
6.Разные предложения могут выражать одну и ту же пропозицию, например,
предложения Сегодня понедельник (сказанное в понедельник) и Вчера был понедельник (сказанное во вторник) выражают одну и ту же пропозицию ( День, на который указывает данное предложение, является понедельником )
7.Высказывания делятся на простые и сложные (составные). Логические соотношения между простыми высказываниями определяются логическими связками, каковые могут иметь в естественном языке следующие соответствия: и, или, следова-
тельно, значит, поскольку, но, так как, если … то и т.д. Например, Если p и q, то s.
8.Пропозициональная и предикатная логики используются для описания логиче-
ской структуры высказываний или рассуждений. В обеих логиках определяют-
ся правила построения сложных высказываний из простых высказываний. В пропозициональной логике внутреннее устройство простых высказываний не учитывается (каждое простое высказывание рассматривается как неделимое целое). В предикатной логике (логике предикатов) внутреннее устройство простых высказываний учитывается.
9.Пропозициональная логика (сентенциональная логика, логика высказываний).
a.Синтаксис 1. Словарь:
•пропозициональные переменные: p, q, g, s...,
• логические связки (логические символы ): , , , 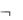
•Скобки (, )
•больше никаких символов в словаре нет
Названия логических символов:
(или &) - конъюнкция (логическое «и»),

- дизъюнкция (логическое «или»), (или ) - импликация (логический условный оператор «если …, то …»), - отрицание («неверно, что …»)
Вместо пропозициональных переменных можно подставлять любые логические высказывания, при этом логическая структура остаѐтся прежней. Например, составляющие p и q, входящие в состав импликации p q можно заменить на конкретные пропозиции: p = ‘идѐт дождь’, q = ‘я беру зонтик’, тогда всѐ выражение будет соответствовать предложению ‘Если идѐт дождь, то я беру зонтик’. Однако на уровне синтаксиса неизвестно, является ли это предложение истинным или ложным.
b.Правильные выражения:
1. Любая пропозициональная переменная является правильным выражением.
2. Если |
и |
- произвольные правильные выражения, то |
, |
, |
, |
||
, ( |
), ( |
), ( |
), ( |
) - также правильные выражения. |
|
|
|
3. Больше никаких правильных выражений нет.
c.Семантика.
Пропозициональные переменные могут принимать лишь одно из двух значений «истина» или «ложь». Часто вместо слова «истина» используют число «1», вместо «ложь» – число «0». Семантику логических связок принято задавать в виде таблиц истинности.
Таблица истинности для конъюнкции:
Значения переменных |
Значение выражения |
||||
|
|
|
|
p |
q |
p |
|
q |
|||
|
|
|
|||
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
Таблица истинности для дизъюнкции: |
||||
Значения переменных |
|
Значение выражения |
|||
|
|
|
|
p |
q |
p |
|
q |
|
||
|
|
|
|
||
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
0 |
|
|
1 |
|
|
|
|
|
|
0 |
|
1 |
|
|
1 |
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
||
|
Таблица истинности для импликации: |
||||
Значения переменных |
|
Значение выражения |
|||
|
|
|
|
p |
q |
p |
|
q |
|
||
|
|
|
|
||
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
|
1 |
|
|
1 |
|
|
|
|
|
|
0 |
|
0 |
|
|
1 |
|
|
|
|
|
|

Таблица истинности для отрицания:
|
Значения переменной p |
|
Значение выражения |
p |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сводная таблица истинности |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
Значения перемен- |
|
Значения выражений |
|
|
||||||
|
|
ных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
q |
p q |
|
p q |
p |
q |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
1 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
0 |
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
0 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Семантика сложных формул строится на основе входящих в их состав простых формул. Например, семантика формулы P (Q 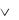 Q) может быть получена в результате построения следующих таблиц истинности:
Q) может быть получена в результате построения следующих таблиц истинности:
Q |
Q |
Q |
|
|
|
1 |
|
1 |
0 |
|
1 |
P |
Q |
Q |
P (Q Q) |
|
|
|
|
1 |
1 |
|
1 |
0 |
1 |
|
0 |
В электронных таблицах Microsoft Office Excel логические операции |
, |
, реали- |
зованы соответственно посредством функций OR, AND, NOT. |
|
|
Существуют и другие логические функции (выразимые через , , |
, |
). Напри- |
мер: |
|
|
строгая дизъюнкция (p q, читается «либо…, либо…»), обозначения: |
|
, |
эквивалентность (p a, читается «если и только если»), обозначения: |
|
или |
штрих Шеффера (p | a, читается «не…или не…», отрицание конъюнкции), стрелка Пирса (p a, читается «ни…, ни…», отрицание дизъюнкции),
10.Возможные миры. Один из вариантов построения семантики логического языка использует понятие «возможный мир». Мы не всегда рассуждаем о том мире, который доступен нашему непосредственному наблюдению. Часто мы говорим о ситуациях в воображаемом или вспоминаемом мире. Например, Если бы сегодня ут-
ром не было дождя, мы поехали бы на прогулку. Для обозначения различных миров
(в том числе и непосредственно наблюдаемого) вводится понятие возможный мир. Предполагается, что для каждой пропозиции можно указать множество всех возможных миров, в которых данная пропозиция истинна. Соответственно, свойства каждого из возможных миров можно характеризовать, указав то множество пропозиций, которые истинны именно в этом мире. Тогда логические связки можно интерпретировать как операции над множествами возможных миров. Например, если Е – универсум, состоящий из всех возможных миров, и пропозиция р истинна в множестве миров А, то закрашенная область соответствует отрицанию пропози-
ции р (то есть р):

Если пропозиция p истинна в множестве миров А, пропозиция q истинна в множестве миров В, то следующие рисунки иллюстрируют соответственно функции p q
иp q:
11.Истинность формулы может оцениваться относительно других формул. На-
пример, если при условии истинности высказываний А и В высказывание С всегда истинно, то говорят, что С логически следует из А и В. Чтобы проверить, связаны ли эти высказывания таким отношением, достаточно построить соответствующие им таблицы истинности.
Например, в наличии соотношения P Q ╞ P можно убедиться по таблице истин-
ности для конъюнкции: из истинности выражения P Q всегда следует истинность
пропозиции P. Именно это соотношение |
и составляет содержание записи |
P Q ╞ P. В наличии соотношения P (Q |
Q) ╞ P можно убедиться, построив |
соответствующие таблицы истинности (см. выше).
12.Формула Р называется тождественно истинной формулой (или тавтологией, или
общезначимой формулой), если Р истинно при любых значениях входящих в неѐ
переменных. Это обозначается так: ╞ Р. Например, ╞ А (В А), ╞ А А В. Аксиомы логики высказываний – это определѐнное подмножество множества общезначимых формулы.
13.Тождественно-истинные формулы логики высказываний называют также законами этой логики. В истинности каждой такой формулы можно убедиться, построив соответствующую ей таблицу истинности.
14.Некоторые законы логики высказываний
a.Закон тождества:
АА
b.Закон отрицания противоречия:
(А А)
c.Закон исключѐнного третьего:
А А
А
d.Законы снятия и введения двойного отрицания:
А А |
А |
А |
e.Законы де Моргана связывают конъюнкцию и дизъюнкцию:
а) отрицание конъюнкции эквивалентно дизъюнкции отрицаний:
¬ (А В) (¬ А ¬ В)
б) отрицание дизъюнкции эквивалентно конъюнкции отрицаний: ¬ (А В) (¬ А ¬ В)
f.Закон контрапозиции устанавливает связь между прямой и обратной импликацией. При переходе от прямой импликации к обратной происходит перестановка членов импликации и замена каждого из них его отрицанием:
(А → В)  (¬ В → ¬ А)
(¬ В → ¬ А)
g.Законы, позволяющие выразить импликацию через дизъюнкцию и отрицание (или конъюнкцию и отрицание):
(А |
В) |
( А |
В) |
(А |
В) |
(А |
В) |

15.Законы логики высказываний – это схемы соотношений. Вместо входящих в их состав пропозициональных переменных можно подставлять любые правильные формулы.
Например, если вместо А подставить p q, а вместо В – p q, то схему
(А → В)  (¬ В → ¬ А),
(¬ В → ¬ А),
выражающую закон контрапозиции, можно переписать так:
(p q → p q)  (¬ (p q) → ¬ (p q))
(¬ (p q) → ¬ (p q))
16.Использование таблиц истинности для характеристики сложных высказываний не всегда удобно: чем сложнее высказывание, тем больше размер таблицы. Например, если сложное высказывание состоит из 10 простых, то таблица истинности будет содержать 1024 строк. Поэтому наряду с табличным методом проверки истинности используется метод, опирающийся на логический вывод одних высказываний из других.
17.Дедуктивное рассуждение. В таком рассуждении из чѐтко сформулированных утверждений (посылок) выводится столь же чѐтко сформулированное утверждение (следствие). Дедуктивное утверждение истинно, если: а) истинны посылки, из которых оно выводится и б) правилен логический вывод.
Для дедуктивных рассуждений большое значение имеет импликация p q, где p – антецедент («предыдущий») импликации, а q – консеквент («последующий»). В классической логике высказываний антецедент и консеквент не обязательно должны быть связаны по смыслу. В неклассических логиках может использоваться строгая импликация, предполагающая наличие такой связи.
A. Примеры правил вывода.
a. Правило отделения, или утверждающий модус (modus ponens, «положитель-
ный способ» ) разрешает из двух высказываний вида А и А→В вывести заключение
В:
А, А → В
В
Горизонтальная черта отделяет заключение от посылок. В качестве посылок выступают антецедент А и сама импликация А → В, заключением служит консеквент импликации.
b. Доказательство от противного (modus tollens, буквально «отрицательный спо-
соб») разрешает из двух высказываний вида А→В и В вывести заключение А:
А → В, В,
А
Здесь в качестве посылок выступают отрицание консеквента В и сама импликация А → В, заключением служит отрицание антецедента импликации.
c. Правило подстановки разрешает любую пропозициональную переменную заменить на любое высказывание. Если исходная формула была истинной, то в результате подстановки также получится истинное высказывание. Например, воспользовавшись законом исключѐнного третьего A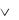 A и подставив (p q) вместо A, можно получить истинное высказывание вида
A и подставив (p q) вместо A, можно получить истинное высказывание вида
(p q)  (p q)
(p q)
B.Доказательство – это конечная последовательность формул F1, F2, ..., Fn, где каждая формула Fi – либо аксиома, либо выводима на основе некоторого правила вывода из предшествующих ей формул Fk, k < i.
C.Различие между доказательством и логическим выводом состоит в следую-
щем:
• при доказательстве посылки рассматриваются как истинные высказывания,

• при логическом выводе – как допущения или гипотезы.
Логический вывод может быть сделан из любых допущений, в том числе из ложных.
D.При аксиоматическом подходе истинность высказываний устанавливается не на основе обращения к их содержаниям, а чисто формально, а именно:
1)аксиомы рассматриваются как исходные формулы, каковые мы полагаем истинными,
2)другие истинные высказывания получаются из аксиом с помощью правил вывода (то есть посредством преобразования одних формул в другие).
18.Индуктивные рассуждения (Ф. Бэкон, Дж. С. Милль). Основа индуктивного рассуждения – обобщение наблюдаемых фактов.
19.Гипотетико-дедуктивный метод (К. Поппер). Рассуждение этого типа включает следующие этапы:
1) выдвижение гипотезы Т,
2) дедуктивный вывод из неѐ проверяемого утверждения о фактах F,
3) фальсификация или верификация первоначальной гипотезы на основе проверки
F. Фальсификация гипотезы Т состоит в выводе из двух посылок T F и F заключения T. Верифицировать гипотезу Т – значит убедиться в истинности некоторого еѐ следствия, то есть консеквента импликации T F. Верификация гипотезы никогда не может быть окончательной, так как всегда есть вероятность обнаружения новых фактов, фальсифицирующих эту гипотезу.
20.Логика высказываний как средство описания электрических схем. Логический элемент компьютера – это схема, реализующая логические операции И, ИЛИ, НЕ. Пропозициональная переменная трактуется как выключатель, который может быть включен (0) или выключен (1). Последовательное соединение двух выключателей
реализует операцию , а параллельное – операцию .
a.В технических приложениях операция конъюнкции называется логическим умножением. Эту операцию можно проиллюстрировать работой следующей электрической цепи (1 означает, что контакт замкнут и ток в цепи есть, 0 – контакт разомкнут и тока в цепи нет):
b.Операцию дизъюнкции в технических приложениях называют логическим сложением. Простейшая электрическая цепь, иллюстрирующая эту операцию, имеет вид:
Тренировочные задания по теме 1.
1.Постройте таблицы истинности для следующих формул пропозициональной логики:
1)А  В
В
2)А  В
В
3)А В
4)А 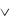 В
В
5)А  В
В

2.Постройте в OpenOffice.org Calc таблицы истинности для логических функций AND, OR: первый столбец используйте для задания значений первого аргумента; второй – для задания значений второго аргумента; в третьем столбце вычислите значение функции для каждой возможной комбинации значений аргументов;
1) вычислите значения логических формул Р Q P и Р Q при разных значениях аргументов.
Q при разных значениях аргументов.
2) введите в две ячейки X и Y числовые значения; в другой ячейке Z вычислите условное значение: если значения в ячейках X и Y одинаковы, то значением ячейки Z будет 1, в противном случае 0.
3) постройте таблицы истинности для следующих логических формул:
а) Р |
Q |
|
б) (Р |
Q) |
(P Q) |
3. Есть ли среди следующих двух рассуждений логически правильный вывод?
Сова и лисица – птицы Следовательно, лисица есть птица
Все киты – млекопитающие Следовательно, все киты – рыбы
4.В следующих фразах выделите простые пропозиции. Опишите смыслы фраз посредством языка логики высказываний:
Если завтра будет снег или завтра будет мороз, то мы не пойдѐм на лыжах.
Если в доме начнут топить, то будет тепло и можно будет не включать обогреватель.
Если отзыв рецензента будет положительный, то редакция пример статью
кпечати, значит, можно будет отдохнуть.
5.Комитет из трѐх человек хочет применить электрическую схему для регистрации тайного голосования простым большинством голосов. Голосующий «за» нажимает кнопку, «нет» – не нажимает. Какая схема может обеспечить возможность такого голосования?
6.Опишите смыслы следующих предложений посредством языка логики высказываний:
Сократ – человек и неверно, что Буцефал - человек
Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка подо льдом блестит
Если это числительное, то оно обозначает количество предметов или их порядок в некоторой последовательности.
Так как мы договорились заранее и установили жѐсткие условия, то не представляется никакой возможности не прибыть на место встречи.
7. Введѐм обозначения для высказываний: Y - «Разговор интересен»;
M – «Иванов ушѐл»;
B– «Петров ушѐл»;
C– «Сидоров ушѐл».
Используйте эти обозначения для построения формулы пропозициональной логики, описывающей смысл высказывания, являющегося отрицанием данного:
Если разговор будет интересным, то никто из участников (ни Иванов, ни Петров, ни Сидоров) не уйдѐт.
Преобразуйте полученную формулу, воспользовавшись одним из законов де Моргана.

8.Допустим, что высказывание А уважает В, но В не уважает А истинно. Исходя из этого факта, определите, какие из следующих высказываний истинны:
Аи В уважают друг друга
Ауважает В, или В не уважает А
Либо В не уважает А, либо А уважает В Неверно, что А и В не уважают друг друга Если А уважает В, то В уважает А Если А не уважает В, то В уважает А Если В не уважает А, то А не уважает В
Ауважает В тогда и только тогда, когда В уважает А
9.Постройте формулы пропозициональной логики, соответствующие смыслу высказываний:
Так как он адвокат, то если он участвует в судебном процессе, он имеет право ознакомиться с материалами следствия.
Если результат умозаключения верен, то либо мы правильно рассуждали, либо получили этот результат случайно.
Все судьи должны быть объективными, так как пристрастные люди допускают ошибки, а объективный человек не бывает пристрастным.
10.Воспользовавшись известными вам законами пропозициональной логики, рассмотрите возможные синонимические преобразования предложений из предыдущего задания.
Тема 2. Множества, бинарные отношения.
Тема 2.1. Множества.
Понятие множества. Виды множеств. Мощность множества. Соотношения между множествами. Изображение множеств с помощью кругов Эйлера (диаграмм Венна). Операции над множествами. Классификации.
Словарь терминов и обозначений по Теме 2.1.
1.Определить некоторое понятие - значит разъяснить его смысл с помощью других, более простых или введенных ранее понятий. Поэтому понятия неизбежно разделяют на определяемые и неопределяемые, считающиеся основными, исходными. Такие понятия можно только пояснить. Понятие множества является одним из важнейших исходных и неопределяемых понятий современной математики. Под множеством понимают совокупность некоторых объектов, объединенных в одно целое по какому-либо признаку и мыслимое как единое целое.
2.Способы задания множеств: а) перечислением: например, А = {0,1,2,3,4,5,6,7,8,9}
– множество цифр; б) заданием общего свойства всех элементов множества, например, множество всех букв латинского алфавита можно определить так: В = {х | х – буква латинского алфавита} .
3.Численность (или мощность) множества М – количество элементов, составляющих множество М, обозначение: М .
4.Пустое множество – множество, не содержащее ни одного элемента, обычно обо-
значается символом ; |
= 0. |
5.Единичное множество – множество, содержащее только один элемент, то есть
М= 1.
6.Конечное множество – множество, содержащее конечное число элементов.

7.Бесконечное множество – множество, содержащее бесконечное число элементов.
8.Чѐткое множество – множество, включающее только такие элементы, принадлежность которых к данному множеству не вызывает сомнений.
9.Нечѐткое множество – множество, включающее элементы, которые могут быть отнесены к этому множеству только с определѐнной степенью вероятности.
10.Нечѐткие множества (fuzzy sets). Это понятие ввѐл американский математик Л. За-
де (L. Zadeh).
Пусть U некоторое множество. Нечѐткое подмножество А U характеризуется
функцией принадлежности μ и определяется так: А = { (х, μА (х)) | х U }
Часто в качестве возможных значений функции μА (х) выбирается интервал [0,1]. Например, можно считать, что μА (а) – это вероятность принадлежности элемента
аU множеству А
Примеры нечѐтких понятий: холодный, красивый, юный, умный, истинный,
правдоподобный.
Например, понятие «истинность»:может иметь такие градации: истинный вполне истинный очень истинный
более или менее истинный очень очень истинный существенно истинный …
Нечѐткие множества – не единственный способ описания смысла нечѐтких понятий. Например, другой способ предложил польский математик Леон Кой (L. Koj). Этот способ основан на выделении свойств, наиболее типичных для объектов, относимых к рассматриваемому нечѐткому понятию. Допустим, что {F1, F2,…, FN}
– набор наиболее типичных свойств объектов, относимых к рассматриваемому понятию А (например, к понятию «игра»). Тогда произвольный элемент а U является элементом рассматриваемого множества А в том и только том случае, когда а обладает хотя бы половиной свойств {F1, F2,…, FN}
11.Круги Эйлера, диаграммы Венна – способы схематичного изображения соотношений между элементами и множествами. Леонард Эйлер (1707-1783), Джон Венн
(1834-1923).
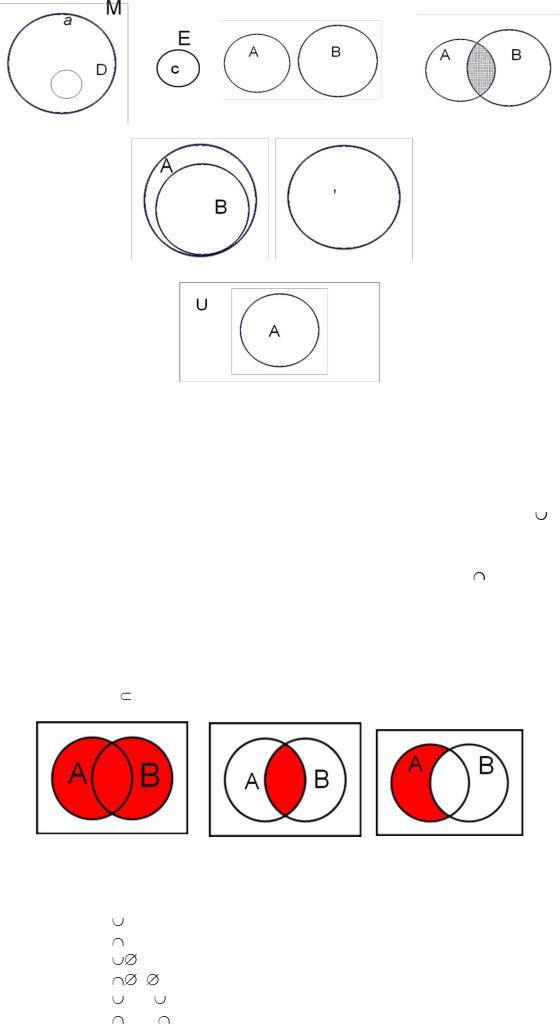
12.Возможные соотношения между элементами и множествами (см. диаграммы ниже).
a. |
Элемент а принадлежит множеству М. Обозначения: а М, с Е. |
|
b. |
Элемент с не принадлежит множеству М, с М. |
|
c. |
Множество D содержится в множестве М. Обозначается D |
М. |
d. |
Множество Е не содержится в множестве М. Обозначается Е |
М. |
e.Множества F и G (а также множества М и Е) не пересекаются, то есть не имеют общих элементов.
f.Множества H и Q имеют общие элементы (заштрихованная часть).
g.Множество В (строго) содержится в множестве А (или «множество В
(строго) включено в множество А», или «множество В является (строгим)
подмножеством множества А). Обозначение: В А.
h.Множества P и R равны. Обозначение: P=R
i.Запись А В означает, что возможно А В и возможно А=В. В этом случае говорят, что множество А нестрого включено в множество В (или «А - не-
строгое подмножество множества В», «А нестрого содержится в В»)/
j.Множество В называют собственным подмножеством множества А, если В А, причѐм В не является пустым множеством и В не совпадает с А.
|
|
G |
|
|
|
|
F |
|
|
|
|
Q |
|
|
|
H |
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
P R
13.Универсальное множество – это множество, относительно которого все рассматриваемые множества являются подмножествами. Дополнение множества А до универсального множества U обозначается Ā
14.Операции над множествами (см. диаграммы ниже).
a. Объединение (или сумма) множеств C и D – это множество P = C D, такое, что: (1) каждый элемент множества C содержится в P; (2) каждый элемент множества В содержится в P; (3) никаких других элементов в P нет.
b. Пересечение множеств А и В – это множество Q = А В, такое, что:
(1)если элемент х содержится как в А, так и в В, то х содержится в Q;
(2)никаких других элементов в Q нет.
c.Разность множеств F и G – это множество R = F \ G, такое, что: (1) если элемент х содержится в F, но не содержится в G, то х содержится в R;
(2)никаких других элементов в R нет.
d.Если H W, то разность W \ H называется дополнением множества H до
|
|
D |
|
|
|
G |
С |
|
|
|
|
||
|
|
F |
||||
|
|
|
|
|
|
|
множества W.
15.Некоторые свойства объединения и пересечения множеств:
АА=А
АА=А
А=А
А=
АВ=В А (коммутативность операции объединения)
АВ=В А (коммутативность операции пересечения)
