Розділ 3. Елементи векторної алгебри

3.1. Основні поняття

Означення. Вектором називають напрямлений відрізок , точка– початок, а точка– кінець. Векторна величина характеризується числовим значенням і напрямом.

Геометрично вектор зображують напрямленим відрізком простору.

Означення. Модулем вектора називається довжина відрізка, який зображує вектор і позначається або.

Означення. Два вектори називаються колінеарними, якщо вони розташовані на одній або на паралельних прямих.

Означення. Два вектори називають рівними, якщо вони колінеарні, напрямлені в одну сторону і мають рівні модулі.

Означення. Вектори називають компланарними, якщо вони розташовані в одній або паралельних площинах.

Означення. Нульовим вектором називається вектор, у якого початок і кінець співпадають.

Модуль нульового вектора дорівнює нулю, а напрям – невизначений.

3.2. Лінійні операції над векторами

1. Додавання векторів.

Означення. Сумою n векторів, розміщених послідовно (початок наступного вектора співпадає з кінцем попереднього), називається вектор, який сполучає початок першого вектор-доданка з кінцем останнього вектор-доданка.

У випадку двох векторів їх суму можна визначити за правилом трикутника або за правилом паралелограма.

Означення. Сумою двох векторів, розташованих послідовно, називається вектор, який з’єднує початок першого з кінцем другого (правило трикутника).

Означення. Сумою двох векторів, які мають спільний початок, називають вектор, що співпадає з діагоналлю паралелограма, побудованого на цих векторах (правило паралелограма).

2. Множення вектора на число.

Означення. Добутком вектора на скаляр називається вектор , модуль якого дорівнює добуткуна, а напрям співпадає з напрямом, якщо, і протилежний напряму, якщо.

Означення. Одиничним вектором (ортом) вектора називається вектор, напрям якого співпадає з напрямом, а модуль дорівнює одиниці.

.

3.3. Проекція вектора на вісь

Означення. Проекцією точки на вісьназивають основуперпендикуляра, опущеного з точкина вісь(рис. 3.).

Означення. Проекцією вектора на вісьназивають модуль вектора, взятий зі знаком „+”, якщо вектор спів напрямлений з віссю, і зі знаком „–”, якщо вектор протилежно напрямлений з віссю(рис. 4.).

Означення. Кутом між вектором і віссю називають найменший кут , на який треба повернути вісь, щоб її напрям співпав з напрямом вектора.

Т е о р е м а. Проекція вектора на вісьдорівнює добутку модуля векторана косинус кута між вектором та віссю.

, .

3.4. Розклад вектора за координатними ортами

Розглянемо у просторі прямокутну систему координат . Нехай– орт осі,– орт осі,– орт осі.

Нехай точка – деяка довільна точка простору. Векторназивають радіус-вектором точки.

Означення. Декартові прямокутні координати точки – це проекції її радіус-векторана осі,і.

.

Позначимо проекції вектора на осі відповідно(абсциса),(ордината),(апліката), тоді

,

,

,

Одержимо .

Вектор можна записати так:

.

Модуль вектора дорівнює.

Позначимо кути, які вектор утворює з координатними осями так:

,

,

(рис. 7).

Маємо тепер ,,.

Косинуси ,,називають напрямленими косинусами радіус-вектора.

, ,.

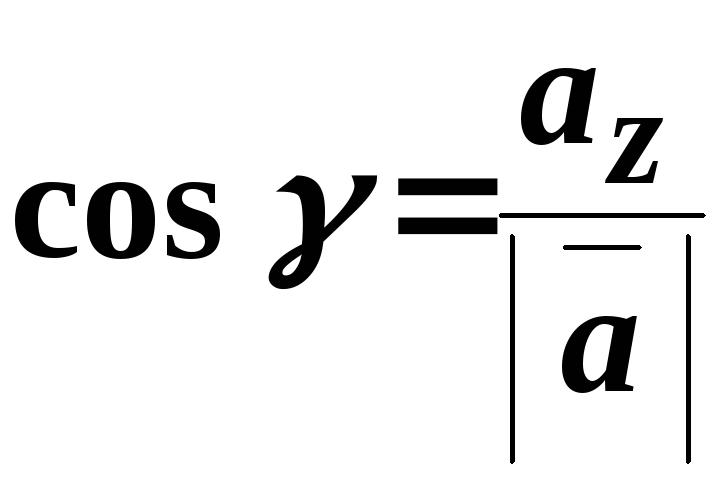Напрямні косинуси задовольняють умову:

.

Зауважимо, якщо ,,

то

,

.