2.4. Гіпербола

Означення. Гіперболою називається геометричне місце точок на площині, абсолютна величина різниці відстаней яких до двох заданих точок – фокусів, є величина стала, дорівнює (менша, ніж відстань між фокусами).

Позначимо відстань між фокусами ічерез.

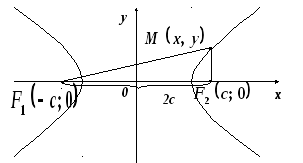
Нехай точка – довільна точка гіперболи, тоді.

,

і

.

Зробивши перетворення, аналогічні тим, що зроблено при виведенні рівняння еліпса маємо:

–канонічне рівняння гіперболи,

де ,

–дійсна вісь гіперболи,

–уявна вісь гіперболи,

–відстань між фокусами,

.

Гіпербола має дві вершини: ,. Точка– центр гіперболи.

Означення. Ексцентриситетом гіперболи називається відношення відстані між фокусами до довжини дійсної осі:

.

Означення. Асимптотою кривої називають таку пряму з властивістю, що точка, яка віддаляється по кривій у нескінченність, необмежено наближається до цієї прямої.

Гіпербола має дві асимптоти:

.

Означення. Директрисами гіперболи називаються дві прямі, перпендикулярні до фокусної (дійсної) осі гіперболи і знаходяться на відстані від центра гіперболи.

–рівняння директрис гіперболи.

Означення. Гіпербола, у якої називаєтьсяр і в н о б і ч н о ю.

Приклад 5.

Скласти рівняння геометричного місця точок, відношення відстаней яких від даної точки і від даної прямоїдорівнює. Рівняння привести до канонічного виду та побудувати криву.

Розв’язання.

В прямокутній декартовій системі координат побудуємо точку та пряму.

Н

у

ехай точка– довільна точка шуканого геометричного місця точок.– перпендикуляр до прямої. Точкамає координати.

За умовою задачі .

Відстані івизначимо за формулою відстані між двома точками на площині:

,

,

тепер маємо:

,

;

;

;

;

.

Ліву і праву частини рівняння розділимо почленно на 5:

.

Одержане рівняння – канонічне рівняння гіперболи. Дійсна піввісь , уявна піввісь.

Визначимо координати фокусів гіперболи: .

Отже, фокуси гіперболи: ,.

Ексцентриситет одержаної гіперболи 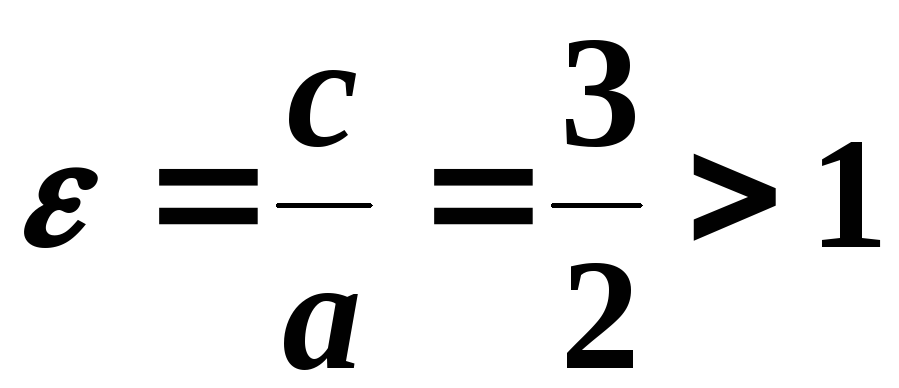. Рівняння асимптот гіперболи мають вид:і.

Отже, і– асимптоти.

Директриса гіперболи: .

Для даного приклада: і– рівняння директрис.

Зробимо рисунок.

2.5. Парабола

Означення. Парабола – геометричне місце точок площини рівновіддалених від даної точки – фокуса і від даної прямої, яка називається директрисою.

Нехай точка – фокус параболи, а пряма– її директриса.

Декартову прямокутну систему координат вибираємо так, щоб вісь проходила через фокус перпендикулярно до прямої, а вісь поділяла б відрізок осі між фокусом і директрисою навпіл.

Позначимо відстань від заданої точки до заданої прямої(директриси) через.

Тоді координати фокуса , рівняння директриси . Нехай – поточна точка. За означенням параболи .

,

,

, звідки

,

отже, – канонічне рівняння параболи,– параметр параболи (відстань від фокуса до директриси). Вершина параболи ділить відстань між фокусом і директрисою навпіл.

Рівняння ,,– канонічні рівняння параболи.

Ексцентриситет параболи дорівнює одиниці: .

Приклад 6.

Дана парабола . Записати рівняння директриси і знайти координати фокуса.

Розв’язання.

Проаналізуємо задане рівняння. – канонічне рівняння параболи, симетричної відносно осі , вітки параболи напрямлені вгору. Точка – вершина параболи,, звідки.

Отже, рівняння директриси , а фокус має координати.