
- •Дьяченко н.К. Аналітична геометрія на площині та у просторі. Елементи векторної алгебри.
- •Розділ 1.
- •Кут між двома прямими. Умова паралельності та перпендикулярності прямих
- •Точка перетину двох прямих
- •Відстань від точки до прямої
- •Питання для самоперевірки
- •Задачі до розділу 1
- •Розділ 2. Криві другого порядку
- •2.1. Поняття кривої другого порядку
- •2.2. Коло
- •2.3. Еліпс
- •2.4. Гіпербола
- •2.5. Парабола
- •2.6. Перетворення декартових координат Паралельне перенесення системи координат
- •Поворот системи координат на кут φ
- •2.7. Побудова кривих другого порядку за їх рівнянням
- •2.8. Графік квадратного тричлена
- •2.9. Графік обернено пропорційної залежності
- •Питання для самоперевірки
- •Задачі до розділу 2
- •Розділ 3. Елементи векторної алгебри
- •3.1. Основні поняття
- •3.2. Лінійні операції над векторами
- •Додавання векторів.
- •Множення вектора на число.
- •3.3. Проекція вектора на вісь
- •3.4. Розклад вектора за координатними ортами
- •3.5. Скалярний добуток векторів та його властивості
- •3.6. Скалярний добуток двох векторів, заданих координатами
- •Питання для самоперевірки
- •Задачі до розділу 3
- •Розділ 4. Аналітична геометрія у просторі
- •Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора
- •Загальне рівняння площини. Дослідження неповного рівняння площини
- •Кут між двома площинами. Умови паралельності та перпендикулярності площин
- •Відстань від точки до площини
- •Рівняння прямої у просторі
- •Кут між двома прямими
- •Перетин прямої з площиною
- •Розділ 5. Сфера
- •Питання для самоперевірки
- •Задачі до розділів 4, 5
- •Бібліографічний список
Розділ 2. Криві другого порядку
2.1. Поняття кривої другого порядку
Означення. Кривою другого порядку називають лінію, що визначається рівнянням другого степеня відносно декартових координат:
![]() ,
,
де
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() –
дійсні числа і
–
дійсні числа і
![]() ,
,
![]() ,
,
![]() одночасно не дорівнюють нулю.
одночасно не дорівнюють нулю.
2.2. Коло
Означення. Коло – геометричне місце точок площини, рівновіддалених від даної точки, що називається центром кола.
Одержимо
рівняння кола з центром в точці
![]() і радіуса
і радіуса
![]() .
.
Нехай
точка
![]() – довільна точка кола.
– довільна точка кола.

Визначимо
відстань між точками
![]() і
і
![]() за формулою відстані між двома точками
на площині:
за формулою відстані між двома точками
на площині:
![]() ,
звідси маємо
,
звідси маємо
|
|
(1) |
канонічне
рівняння кола з центром в точці
![]() радіуса
радіуса
![]() .
.
Коло
радіуса
![]() ,
центр якого знаходиться в початку
координат описується рівнянням:
,
центр якого знаходиться в початку
координат описується рівнянням:
|
|
(2) |
Якщо в рівнянні (1) розкрити дужки, то одержимо рівняння кола у вигляді:
|
|
(3) |
Як бачимо, для рівняння кола виконуються дві умови:
коефіцієнти при
 і
і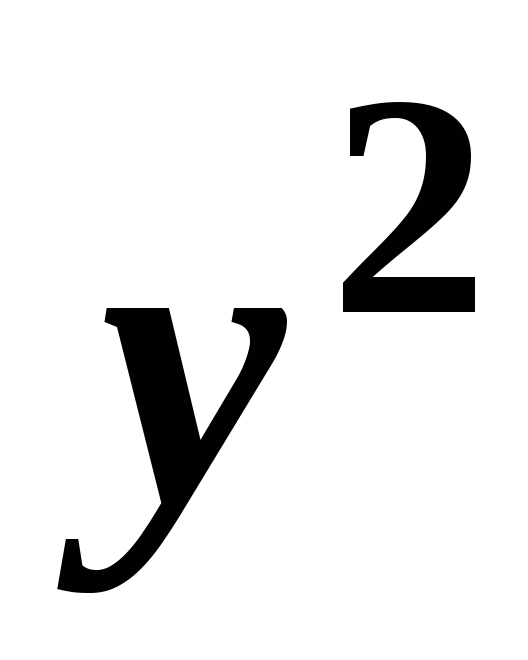 рівні;
рівні;відсутній член з добутком координат х ∙ у.
Приклад 2.
Знайти
центр і радіус кола
![]() .
.
Розв’язання.
Перетворимо
ліву частину рівняння, виділимо для
цього повні квадрати по змінним
![]() і
і![]() .
.
![]() ,
,
![]() .
.
![]() –рівняння
кола з центром в точці
–рівняння
кола з центром в точці
![]() радіуса
радіуса![]() .
.
2.3. Еліпс
Означення. Еліпсом називається геометричне місце точок площини, сума відстаней від кожної з яких до двох заданих точок (фокусів), є величина стала, дорівнює 2а, більша, ніж відстань між фокусами.
Позначимо
відстань між фокусами
![]() і
і
![]()
![]() .
.
Виберемо
систему координат так, щоб фокуси мали
координати
![]() і
і![]()

Нехай
точка
![]() –
довільна точка еліпса. За визначенням
еліпса маємо:
–
довільна точка еліпса. За визначенням
еліпса маємо:
![]() .
.
![]() ;
;
![]() ,
,
тоді
![]() ,
,
![]() .
.
Ліву і праву частини останнього рівняння піднесемо до квадрату:
![]() ,
,
![]() ,
,
звідки
![]() ,
,
або
![]() ,
,
тоді
![]() ,
,
![]() .
.
Згідно
з умовою в означенні еліпса
![]() ,
отже
,
отже![]() .
.
Позначимо
![]() .
Тоді рівняння перепишеться:
.
Тоді рівняння перепишеться:
![]() ,
або
,
або ![]() – канонічне рівняння еліпса.
– канонічне рівняння еліпса.
Еліпс, заданий канонічним рівнянням, симетричний відносно осей координат:
![]() –велика
вісь еліпса,
–велика
вісь еліпса,
![]() –мала
вісь еліпса,
–мала
вісь еліпса,
![]() –відстань
між фокусами,
–відстань
між фокусами,
![]() ,
,
точка
![]() – центр еліпса.
– центр еліпса.
Точки перетину еліпса з осями називаються вершинами еліпса.
Отже, еліпс має чотири вершини:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.

Означення. Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великої осі.
![]() .
.
Оскільки
![]() ,
то
,
то![]() .
.
Ексцентриситет
характеризує форму еліпса: якщо
![]() ,
то еліпс сплющується.
,
то еліпс сплющується.
Означення.
Директрисами
еліпса
називають дві прямі, перпендикулярні
до фокальної осі еліпса і розміщенні
симетрично відносно центра еліпса на
відстані
![]() від нього. Директриси еліпса
від нього. Директриси еліпса![]() мають рівняння
мають рівняння![]() .
.
Приклад 3. Побудувати, виписати основні числові характеристики:
![]() .
.
Розв’язання. Дане рівняння є канонічним рівнянням еліпса.
![]() ,
,
![]() – велика піввісь;
– велика піввісь;![]() ,
,![]() –
мала піввісь.
–
мала піввісь.
Побудуємо
прямокутну декартову систему координат
на площині. Вздовж осі
![]() вліво і вправо від початку системи
координат відкладемо відстань
вліво і вправо від початку системи
координат відкладемо відстань
![]() ,
а вздовж осі
,
а вздовж осі
![]() вгору
і вниз – відстань
вгору
і вниз – відстань
![]() .
.
х
Вершини еліпса мають координати:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Визначимо
параметр
![]() :
:
![]() .
.
Фокуси
лежать на осі
![]() на
відстані
на
відстані
![]() від центра еліпса і мають координати
від центра еліпса і мають координати![]() ,
,![]() .
.
Ексцентриситет
еліпса
![]() .
.
Директриси
мають рівняння:
![]() .
.
 ,
звідси
,
звідси
![]() .
.
Приклад 4.
Скласти
канонічне рівняння еліпса, що проходить
через точку
![]() і має велику піввісь
і має велику піввісь![]() .
.
Розв’язання.
Канонічне рівняння еліпса має вид:
![]() .
.
З урахуванням,
що велика піввісь
![]() ,
рівняння перепишеться
,
рівняння перепишеться![]() .
.
Оскільки
точка
![]() належить еліпсу, то її координати повинні
задовольняти останньому рівнянню. Отже,
належить еліпсу, то її координати повинні
задовольняти останньому рівнянню. Отже,![]() .
.
Визначимо
звідси:
![]() .
.
Тепер запишемо шукане канонічне рівняння еліпса:
![]() .
.
