
- •Дьяченко н.К. Аналітична геометрія на площині та у просторі. Елементи векторної алгебри.
- •Розділ 1.
- •Кут між двома прямими. Умова паралельності та перпендикулярності прямих
- •Точка перетину двох прямих
- •Відстань від точки до прямої
- •Питання для самоперевірки
- •Задачі до розділу 1
- •Розділ 2. Криві другого порядку
- •2.1. Поняття кривої другого порядку
- •2.2. Коло
- •2.3. Еліпс
- •2.4. Гіпербола
- •2.5. Парабола
- •2.6. Перетворення декартових координат Паралельне перенесення системи координат
- •Поворот системи координат на кут φ
- •2.7. Побудова кривих другого порядку за їх рівнянням
- •2.8. Графік квадратного тричлена
- •2.9. Графік обернено пропорційної залежності
- •Питання для самоперевірки
- •Задачі до розділу 2
- •Розділ 3. Елементи векторної алгебри
- •3.1. Основні поняття
- •3.2. Лінійні операції над векторами
- •Додавання векторів.
- •Множення вектора на число.
- •3.3. Проекція вектора на вісь
- •3.4. Розклад вектора за координатними ортами
- •3.5. Скалярний добуток векторів та його властивості
- •3.6. Скалярний добуток двох векторів, заданих координатами
- •Питання для самоперевірки
- •Задачі до розділу 3
- •Розділ 4. Аналітична геометрія у просторі
- •Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора
- •Загальне рівняння площини. Дослідження неповного рівняння площини
- •Кут між двома площинами. Умови паралельності та перпендикулярності площин
- •Відстань від точки до площини
- •Рівняння прямої у просторі
- •Кут між двома прямими
- •Перетин прямої з площиною
- •Розділ 5. Сфера
- •Питання для самоперевірки
- •Задачі до розділів 4, 5
- •Бібліографічний список
Міністерство аграрної політики України
Дніпропетровський державний аграрний університет
Дьяченко н.К. Аналітична геометрія на площині та у просторі. Елементи векторної алгебри.
Навчальний посібник
Дніпропетровськ
2009
Дьяченко Н.К.
Аналітична геометрія на площині та у просторі. Елементи векторної алгебри:
Навчальний посібник/ Дніпропетровський державний аграрний університет – Дніпропетровськ, 2009 – 78 с.
У навчальному посібнику розглянуто основні поняття і положення аналітичної геометрії на площині та у просторі, а також елементи векторної алгебри.
Розібрано типові задачі, а також наведені завдання для самостійного розв’язування.
Посібник буде корисним для студентів заочної форми навчання економічних спеціальностей, а також для студентів очної форми навчання при підготовці до модульної роботи з аналітичної геометрії.
Розділ 1.
ПРЯМА НА ПЛОЩИНІ
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ НА ПЛОЩИНІ
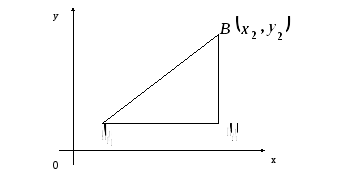
Нехай
задано точки
![]() і
і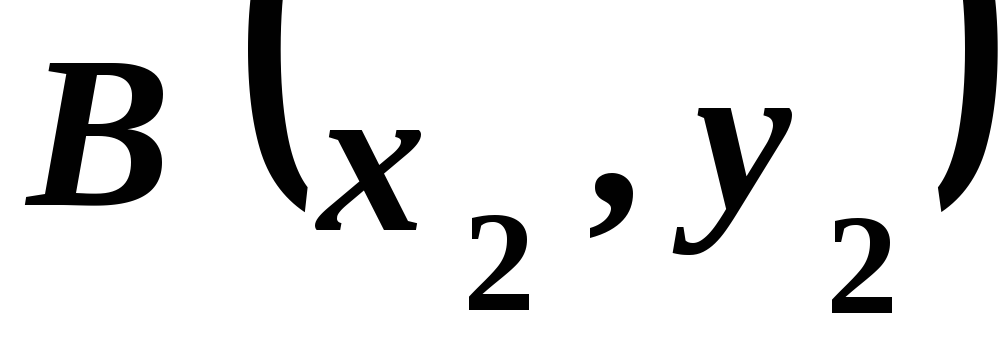 .
Визначимо відстань між ними.
.
Визначимо відстань між ними.
З
![]() маємо:
маємо:
![]() .
.
Отже, відстань між двома точками на площині
![]()
Відстань
точки
![]() від початку координат знаходимо за
формулою
від початку координат знаходимо за
формулою![]() .
.
ДІЛЕННЯ ВІДРІЗКА В ЗАДАНОМУ ВІДНОШЕННІ
Дано
точки
![]() та
та![]() .
.
Вимагається
знайти координати точки ![]() ,
яка ділить відрізок
,
яка ділить відрізок![]() у відношенні
у відношенні![]() ,
тобто
,
тобто
![]() .
.
Координати
точки
![]() можна визначити за формулами:
можна визначити за формулами:
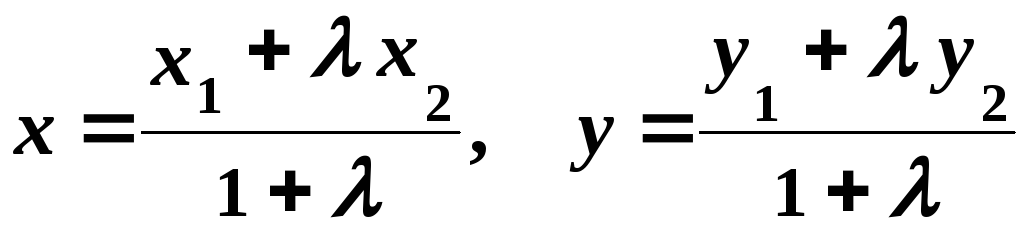 .
.
Зауваження.
Координати
середини відрізка
![]() знаходимо за формулами
знаходимо за формулами
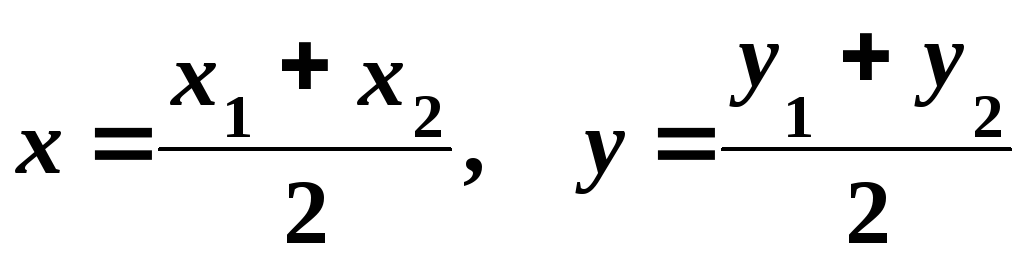 .
.
ПОНЯТТЯ РІВНЯННЯ ЛІНІЇ НА ПЛОЩИНІ
Нехай
на площині задано декартову прямокутну
систему координат
![]() і деяку лінію
і деяку лінію
![]() .
.
Означення.
Рівняння
![]() називаютьрівнянням
лінії
(відносно заданої системи координат),
якщо рівняння задовольняється координатами
називаютьрівнянням
лінії
(відносно заданої системи координат),
якщо рівняння задовольняється координатами
![]() і
і
![]() будь-якої точки, яка лежить на лінії і
не задовольняється координатами
будь-якої точки, яка лежить на лінії і
не задовольняється координатами
![]() і
і
![]() жодної
точки, що не лежить на лінії
жодної
точки, що не лежить на лінії ![]() .
.
РІВНЯННЯ ПРЯМОЇ НА ПЛОЩИНІ
Рівняння прямої з кутовим коефіцієнтом.
Означення.
Кутом
нахилу
прямої до осі
![]() називається кут між прямою та віссю
називається кут між прямою та віссю
![]() ,
який відраховується проти годинникової
стрілки від додатного напряму осі
,
який відраховується проти годинникової
стрілки від додатного напряму осі
![]() до прямої.
до прямої.
Означення.
Кутовим
коефіцієнтом прямої
називається тангенс кута нахилу цієї
прямої до осі
![]() ,
тобто
,
тобто
![]() .
.

![]()
Рівняння прямої з кутовим коефіцієнтом має вид:
|
|
(1) |
Числовий
параметр
![]() називаютьпочатковою
ординатою.
Параметр
називаютьпочатковою
ординатою.
Параметр
![]() дорівнює ординаті точки перетину прямої
з віссю
дорівнює ординаті точки перетину прямої
з віссю
![]() .
.
Розглянемо деякі частинні випадки.
Якщо
 ,
то рівняння(1)
має
вигляд
,
то рівняння(1)
має
вигляд
 – рівняння прямої, що проходить через
початок системи координат.
– рівняння прямої, що проходить через
початок системи координат.
Якщо
 ,
то рівняння(1)
має
вигляд
,
то рівняння(1)
має
вигляд
 – рівняння прямої, паралельної осі
– рівняння прямої, паралельної осі
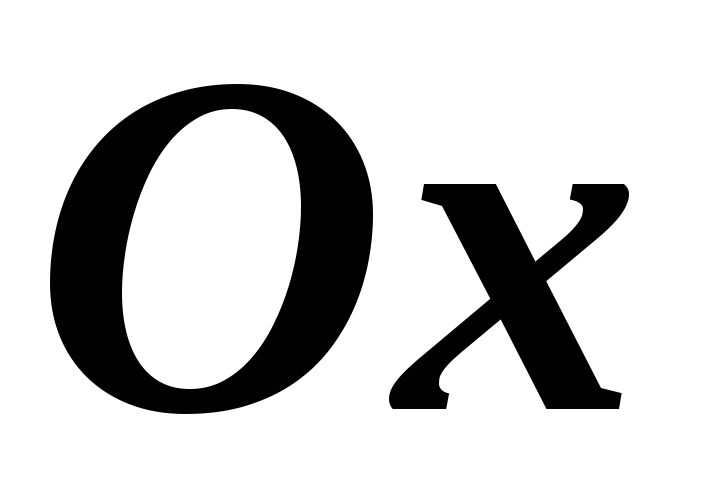 .
.
Якщо
 ,
то рівняння(1)
має
вигляд
,
то рівняння(1)
має
вигляд
 – рівняння осі
– рівняння осі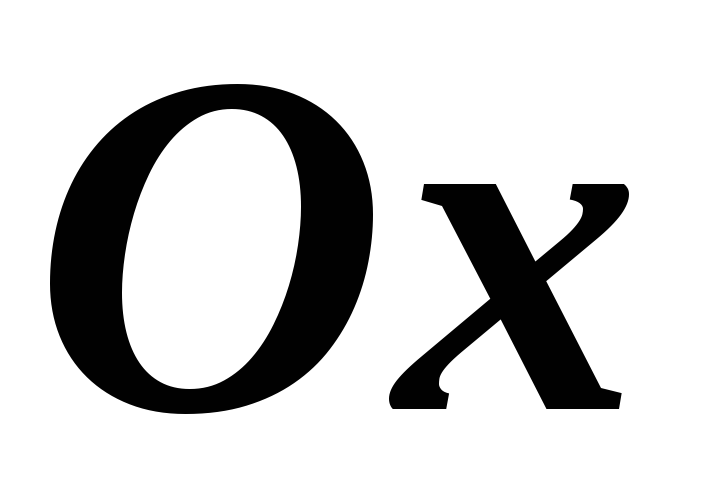 .
.
Загальне рівняння прямої.
Т е о
р е м а.
Кожне рівняння першого ступеня відносно
х і у,
тобто рівняння виду
![]() ,
визначає на площині пряму лінію.
,
визначає на площині пряму лінію.
Рівняння
|
|
(2) |
називають загальним рівнянням прямої.
![]() ,
,
![]() ,
,![]() – числові параметри, причому
– числові параметри, причому![]() .
.
Частинні випадки.
1)
![]() ,
,![]() .
Рівняння(2)
тоді матимемо вид
.
Рівняння(2)
тоді матимемо вид
![]() – рівняння прямої, що проходить через
початок системи координат.
– рівняння прямої, що проходить через
початок системи координат.
2)
![]() ,
,![]() .
Пряма визначається рівнянням
.
Пряма визначається рівнянням![]() ,
або
,
або – пряма, яка паралельна осі
– пряма, яка паралельна осі
![]() .
.
3)
![]() ,
,![]() .
В цьому випадку рівняння(2)
буде мати вид
.
В цьому випадку рівняння(2)
буде мати вид
![]() ,
звідки
,
звідки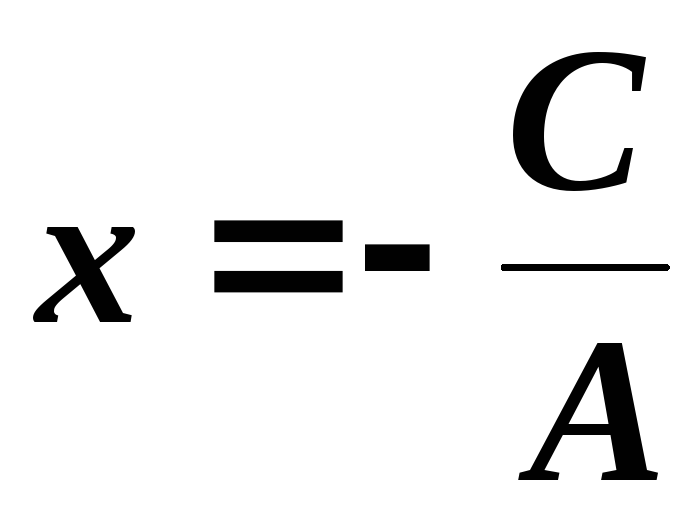 – рівняння прямої, паралельної осі
– рівняння прямої, паралельної осі
![]() .
.
4)
![]() ,
,![]() ,
рівняння(2)
має вигляд:
,
рівняння(2)
має вигляд:
![]() –рівняння
осі
–рівняння
осі
![]() .
.
5)
![]() ,
,![]() ,
рівняння(2)
має вигляд:
,
рівняння(2)
має вигляд:
![]() –рівняння
осі
–рівняння
осі
![]() .
.
Рівняння прямої, що проходить через задану точку в заданому напрямі.
Нехай
задано точку
![]() ,
через яку проходить пряма і кутовий
коефіцієнт
,
через яку проходить пряма і кутовий
коефіцієнт![]() цієї прямої, тоді рівняння
цієї прямої, тоді рівняння
|
|
(3) |
називають рівнянням прямої, що проходить через задану точку в заданому напрямі.
Рівняння прямої, що проходить через дві задані точки.
Нехай
задано точки
![]() і
і![]() .
Вимагається скласти рівняння прямої,
що проходить через ці точки.
.
Вимагається скласти рівняння прямої,
що проходить через ці точки.
Використаємо
рівняння (3).
Підставимо в це рівняння координати
точки
![]() .
.
Маємо
![]() ,
звідки
,
звідки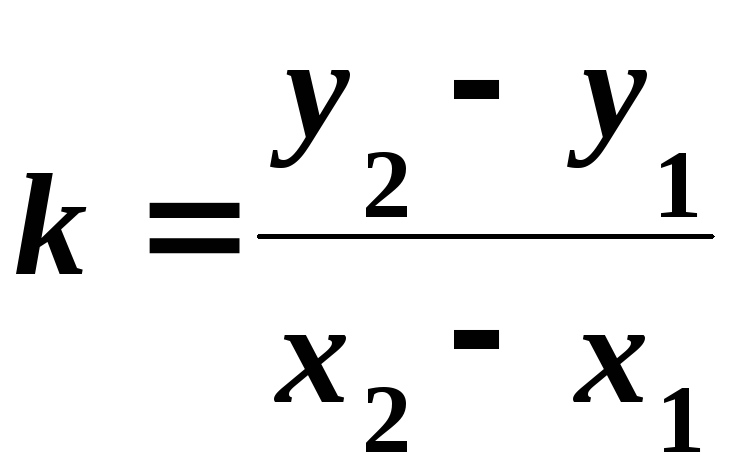 – кутовий коефіцієнт прямої, яка
проходить через дві задані точки.
– кутовий коефіцієнт прямої, яка
проходить через дві задані точки.
Підставимо цей кутовий коефіцієнт в рівняння (3).
Дістанемо
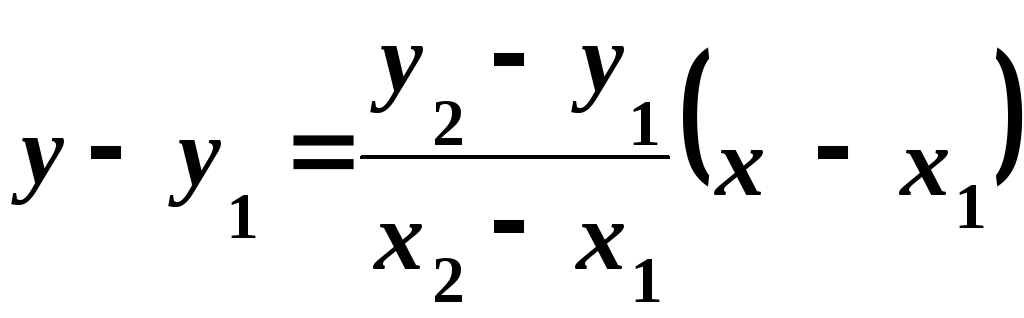 ,
,
звідки
|
|
(4) |
рівняння прямої, що проходить через дві задані точки.
В рівнянні
(4)
припускаємо, що
![]() ,
,![]() ,
інакше, це рівняння не має змісту.
,
інакше, це рівняння не має змісту.
Якщо
![]() ,
то будемо мати
,
то будемо мати![]() – пряма, паралельна осі ординат.
– пряма, паралельна осі ординат.
Якщо
![]() ,
то маємо пряму
,
то маємо пряму![]() – пряма паралельна осі абсцис.
– пряма паралельна осі абсцис.
Рівняння прямої у відрізках на осях.
Рівняння прямої у відрізках на осях має вид:
|
|
(5) |
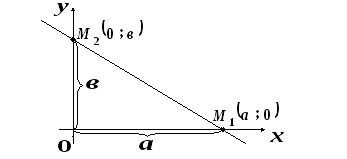
Параметр
![]() в
цьому рівнянні – абсциса точки перетину
прямої з віссю
в
цьому рівнянні – абсциса точки перетину
прямої з віссю
![]() ,
,
![]() – ордината
точки перетину прямої з віссю
– ордината
точки перетину прямої з віссю
![]() .
.


