1.12. Несимметричная нагрузка трехфазных трансформаторов. Метод симметричных составляющих

В электрических системах идеальная симметричная нагрузка практически не встречается. Согласно стандарту трехфазная система токов считается практически симметричной, если при разложении ее на векторы прямой и обратной последовательности оказывается, что величина векторов обратной последовательности не превышает 5 % величины векторов прямой последовательности.

Отклонения от симметрии увеличиваются при увеличении мощности однофазных или двухфазных потребителей, питаемых от трехфазной сети, и наиболее существенны при несимметричных коротких замыканиях, отключении одной из фаз и др.

При анализе несимметричных режимов работы оборудования пользуются методом симметричных составляющих, предложенным Чарльзом Фортескью в 1918 г. Согласно методу любую несимметричную трехфазную систему, например систему токов ,иможно разложить на три симметричные системы токов: прямой (индекс 1), обратной (индекс 2) и нулевой (индекс 0) последовательности, см.рисунок 1.11:

.

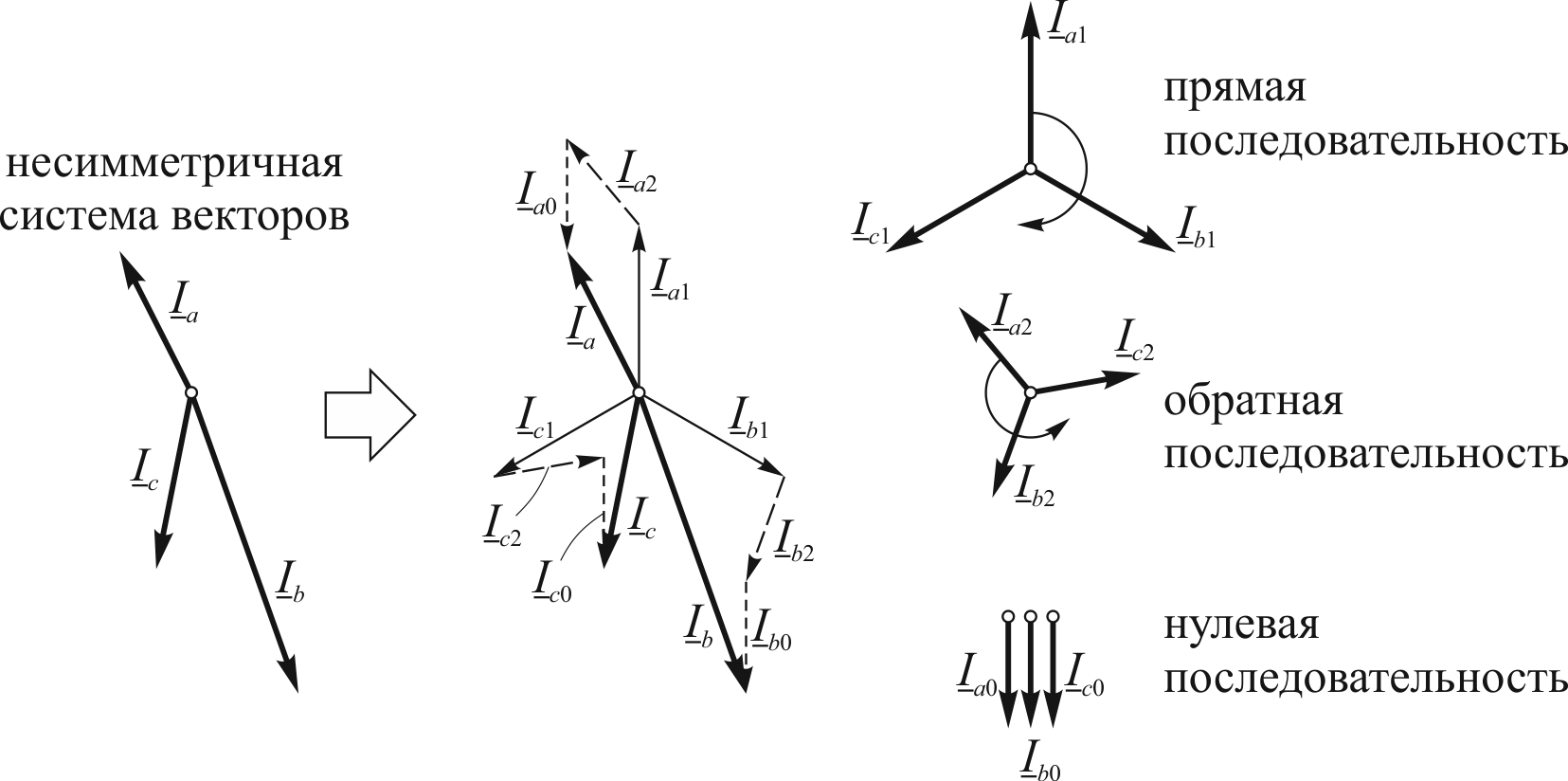
Рис. 1.11. Представление несимметричной системы токов (,,) на комплексной плоскости в виде суммы симметричных составляющих прямой (,,), обратной (,,) и нулевой (,,) последовательностей.

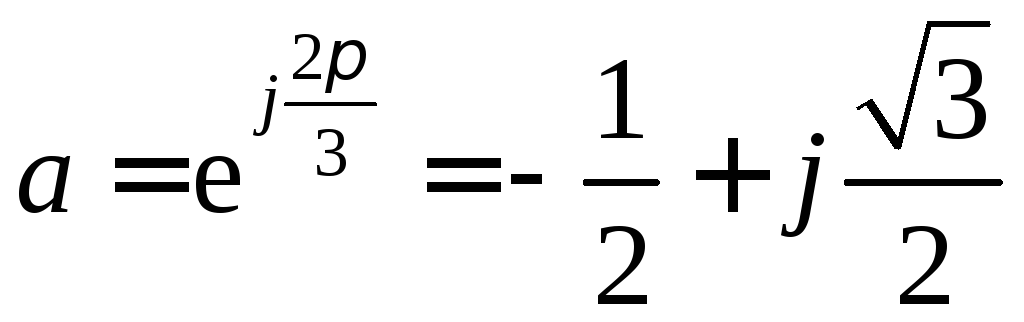Величины одной последовательности отличаются между собой только фазовыми углами, равными или 120°. Введем оператор поворота вектора на комплексной плоскости:

и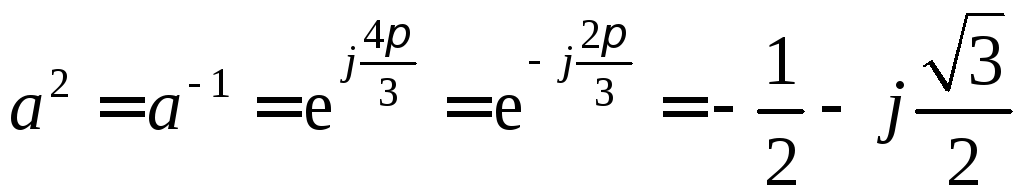. Симметричные составляющие

нулевой последовательности	прямой последовательности	обратной последовательности

Тогда

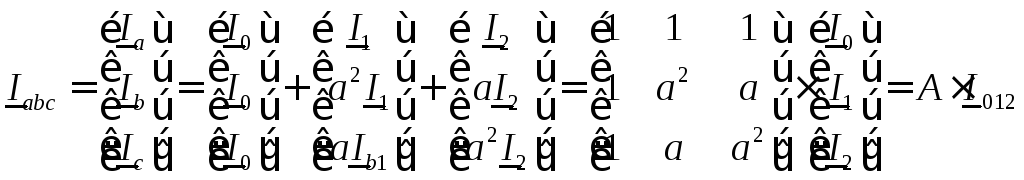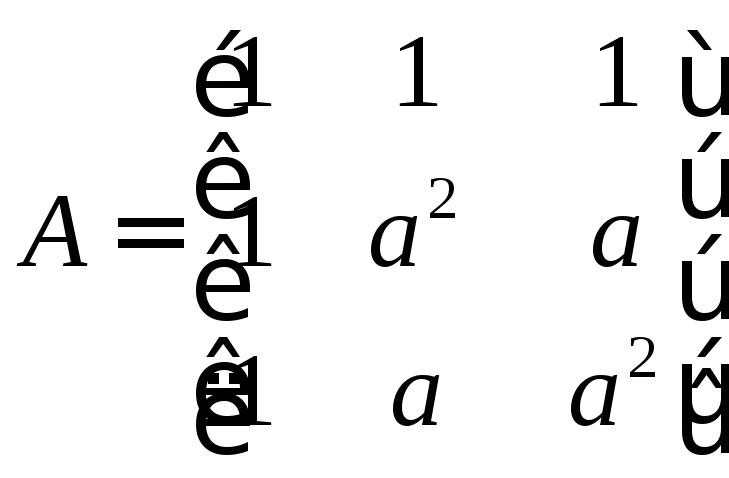, где и .

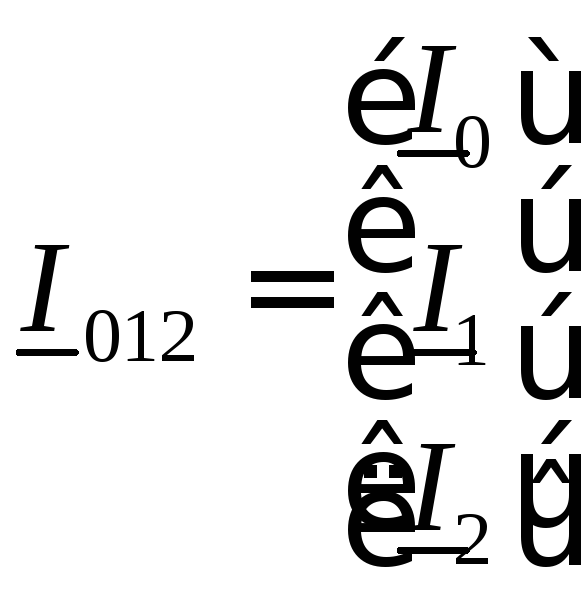Соответствующие симметричные составляющие определяются следующим образом:

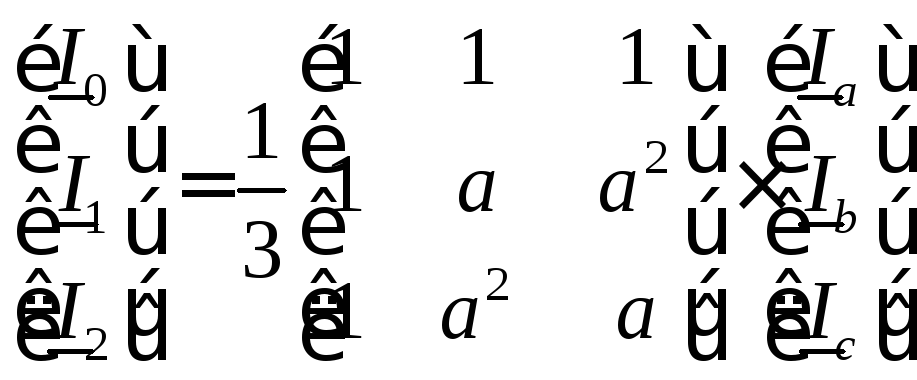или, где

.

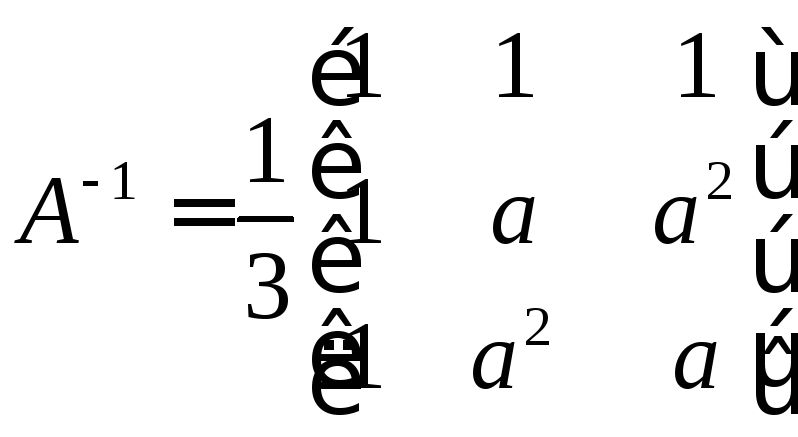Метод симметричных составляющих основан на принципе наложения, поэтому его применение к анализу работы трансформатора ограничено случаем ненасыщенной магнитной цепи ().

1.13. Схемы замещения и сопротивления трансформатора для токов прямой и обратной последовательностей

Любое симметричное статическое (без вращающихся частей) трехфазное устройство: трансформатор, линия электропередачи, электрическая печь и т.д., – имеет равные сопротивления для симметричных составляющих прямой и обтарной последовательностей. Порядок чередования фаз не имеет значения, поэтому внешний вид схемы замещения одной фазы трансформатора для токов обратной последвоательности совпадает со схемой для токов прямой последовательности, рассмотренной ранее (см. рисунок 1.3).

При отсутствии токов нулевой последовательности, в случае, если нулевого провода нет или если этот провод не нагружен током, действие токов прямой и обратной последовательности можно учитывать совместно без разложения величин на сумму составляющих прямой, обратной и нулевой последовательностей. Необходимость в таком разложении возникает только при наличии токов нулевой последовательности.

1.14. Схемы замещения и сопротивления трансформатора для токов нулевой последовательности

Для токов нулевой последовательности могут быть предложены аналогичные Т-образные схемы замещения, что и для токов прямой и обратной последовательностей. Вид схемы замещения и сопротивление нулевой последовательности в целом зависит от схемы соединения обмоток, см. рисунок 1.12. Параметры отдельных элементов схемы замещения зависят от устройства магнитной цепи, но не зависят от схемы соединения обмоток.

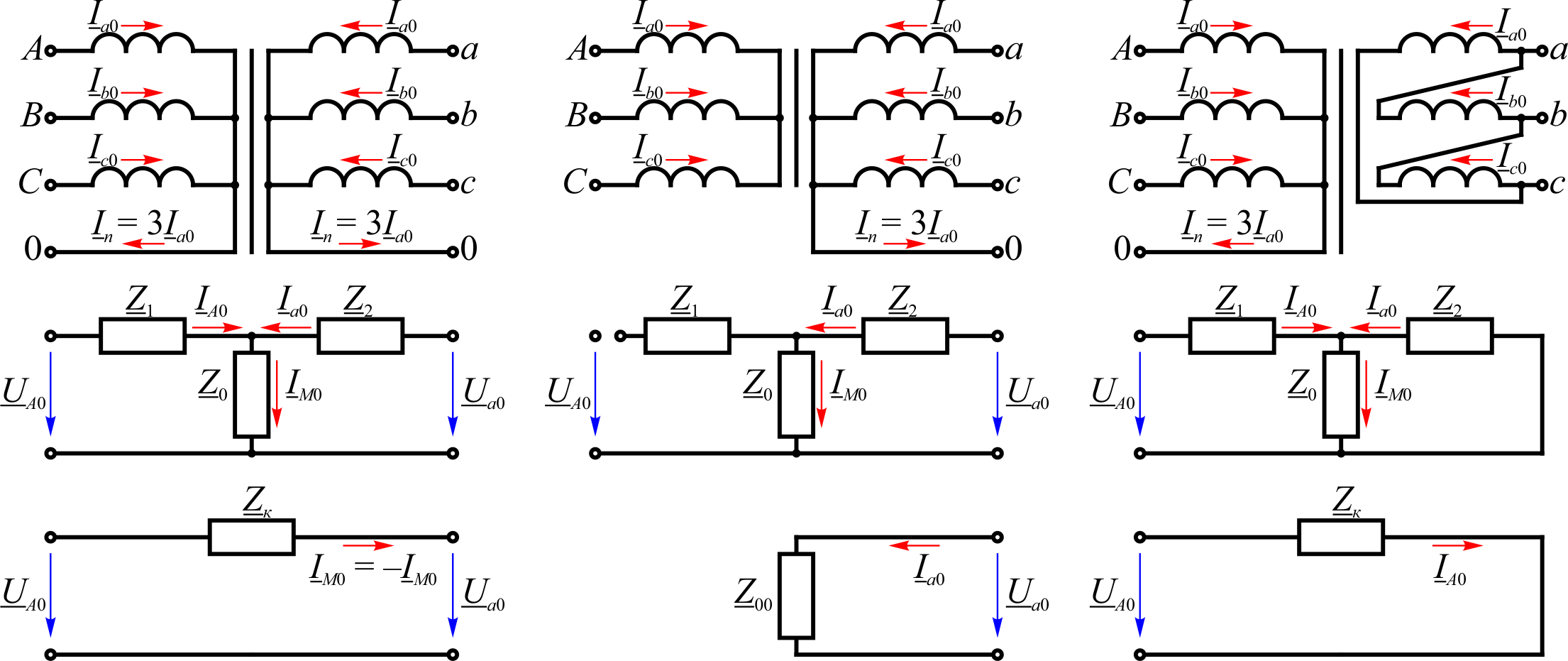
Рис. 1.12. Схемы замещения трансформатора для токов нулевой последовательности.

При соединении обмотки в звезду с нулевым проводом Y₀ ток нулевой последовательности может существовать в этой обмотке и во внешней цепи. При заземлении нулевой точки роль нулевого провода играет земля. Поэтому схема замещения для токов нулевой последовательности со стороны этой обмотки не отличается по внешнему виду от схемы замещения прямой последовательности.

При соединении обмотки в звезду без нулевого провода Y ток нулевой последовательности в этой обмотке и во внешней цепи сущестсовать не может. Схема замещения нулевой последовательности со стороны этой обмотки разомкнута, см. рисунок 1.12.

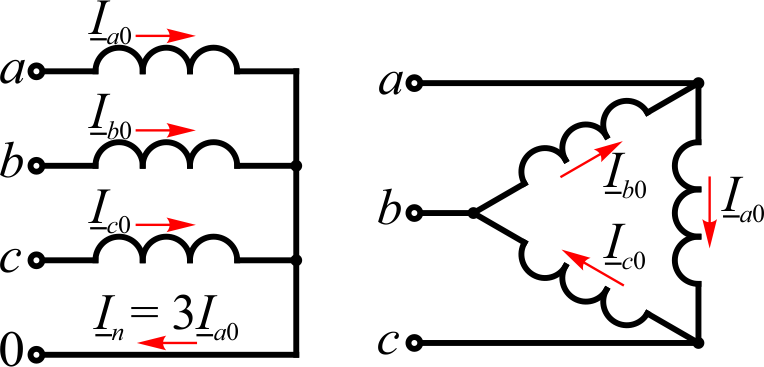
Рис. 1.13. Путь протекания токов нулевой последовательности в обмотках, соединенных в звезду с нейтральным проводом и в треугольник.

Обмотка, соединенная в треугольник Δ, является короткозамкнутой по отношению к токам нулевой последовательности. Токи нулевой последовательности циркулируют внутри замкнутого треугольного контура и отсутствуют в линейных проводах, как показано на рисунке 1.13. Схема замещения нулевой последовательности изображается со стороны этой обмотки замкнутой накоротко, см. рисунок 1.12.