
MetodTM1
.pdfТаблица 1.2
Исходные данные для задания С2. Равновесие пространственной системы сил
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
варианта |
||||||||||
задания |
|
|
|
|
|
|
|
|
|
|
P, кН |
5 |
4 |
6 |
10 |
16 |
15 |
12 |
10 |
15 |
14 |
F, кН |
8 |
6 |
12 |
6 |
10 |
10 |
8 |
12 |
12 |
10 |
Q, кН |
– |
12 |
– |
12 |
8 |
12 |
10 |
– |
10 |
12 |
M, кН·м |
12 |
– |
10 |
8 |
12 |
6 |
8 |
6 |
8 |
– |
α, град |
60 |
30 |
30 |
30 |
60 |
60 |
60 |
30 |
30 |
60 |
a, м |
1,2 |
0,8 |
1,4 |
0,6 |
1,2 |
0,9 |
1,4 |
0,4 |
0,8 |
0,8 |
b, м |
1,0 |
0,6 |
1,1 |
0,4 |
0,8 |
0,4 |
0,6 |
1,2 |
0,2 |
0,6 |
c, м |
0,8 |
0,5 |
0,8 |
0,3 |
1,4 |
0,8 |
1,2 |
0,8 |
0,4 |
0,4 |
d, м |
0,4 |
0,4 |
0,6 |
0,2 |
0,4 |
0,2 |
0,4 |
0,6 |
0,6 |
0,6 |
|
|
|
|
|
|
|
|
|
|
|
Номер |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
варианта |
||||||||||
задания |
|
|
|
|
|
|
|
|
|
|
P, кН |
8 |
10 |
10 |
15 |
14 |
10 |
16 |
9 |
10 |
12 |
F, кН |
6 |
12 |
16 |
8 |
12 |
14 |
10 |
15 |
8 |
10 |
Q, кН |
– |
14 |
– |
10 |
10 |
12 |
14 |
– |
12 |
14 |
M, кН·м |
10 |
– |
12 |
12 |
12 |
8 |
10 |
10 |
10 |
– |
α, град |
30 |
60 |
60 |
60 |
30 |
30 |
30 |
60 |
60 |
30 |
a, м |
0,8 |
1,3 |
0,9 |
0,5 |
1,3 |
1,2 |
1,6 |
0,6 |
0,9 |
1,2 |
b, м |
0,6 |
1,1 |
0,6 |
0,4 |
0,9 |
0,6 |
0,8 |
1,2 |
0,3 |
0,8 |
c, м |
0,4 |
0,8 |
0,5 |
0,2 |
1,5 |
0,9 |
1,2 |
0,4 |
0,6 |
0,6 |
d, м |
0,2 |
0,4 |
0,4 |
0,1 |
0,5 |
0,4 |
0,6 |
0,2 |
0,2 |
0,8 |
|
|
|
|
|
|
|
|
|
|
|
Номер |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
варианта |
||||||||||
задания |
|
|
|
|
|
|
|
|
|
|
P, кН |
10 |
12 |
5 |
8 |
10 |
14 |
18 |
12 |
14 |
10 |
F, кН |
12 |
8 |
15 |
10 |
12 |
8 |
10 |
15 |
9 |
8 |
Q, кН |
– |
10 |
– |
12 |
14 |
10 |
16 |
– |
12 |
6 |
M, кН·м |
12 |
– |
16 |
14 |
8 |
10 |
8 |
12 |
10 |
– |
α, град |
90 |
30 |
60 |
30 |
45 |
30 |
30 |
60 |
60 |
30 |
a, м |
0,6 |
0,8 |
1,1 |
1,2 |
1,5 |
0,8 |
1,0 |
0,8 |
1,2 |
0,9 |
b, м |
0,8 |
0,6 |
0,9 |
1,0 |
0,9 |
0,6 |
0,8 |
1,4 |
0,6 |
0,4 |
c, м |
0,4 |
1,2 |
0,8 |
0,6 |
1,5 |
0,9 |
1,1 |
0,5 |
0,8 |
0,6 |
d, м |
0,4 |
1,5 |
0,5 |
0,2 |
0,4 |
0,3 |
0,3 |
0,4 |
0,6 |
0,5 |
20
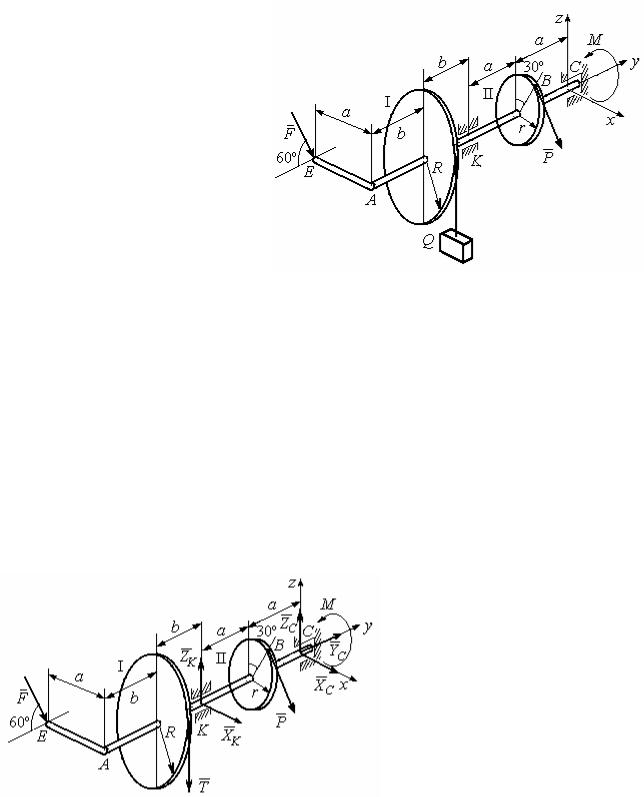
Примеры решения задания С2. Равновесие пространственной системы сил
Задача 1. Горизонтальный вал (рис. 1.14) закреплен в подпятнике С и
подшипнике К. Вал имеет шкив I радиуса R и шкив II ра-
диуса r, перпендикулярные оси вала. Рукоять АЕ парал-
лельна оси Сx. Нить, удержи-
вающая груз Q, сходит со шкива I по касательной верти-
кально вниз. На вал действуют
силы F, P и пара сил с мо-
Рис. 1.14. Схема вала и его нагрузка
ментом М, закручивающая вал
вокруг оси Сy. Сила F находится в плоскости, параллельной zCy, и составляет угол 60° с направлением оси Cy. Сила P приложена в точке В шкива II, опре-
деляемой центральным углом 30º, и направлена по касательной. Определить ве-
личину уравновешивающего момента М и реакции подшипника и подпятника,
если Р = 4 кН, F = 2 кН, Q = 3 кН, R = 0,6 м, r = 0,3 м, а = 0,8 м, b = 0,4 м. |
|
||
Решение |
|
|
|
Рассмотрим равновесие вала. На вал действуют внешние силы |
F , P , па- |
||
|
ра сил с моментом М и реак- |
||
|
ции связей. Связями являют- |
||
|
ся нить, натянутая грузом |
Q , |
|
|
подпятник С и подшипник К. |
||
|
Освобождаем вал от связей, |
||
|
заменяя их действие реак- |
||
|
циями. Реакцию подпятника |
||
Рис. 1.15. Внешние силы и реакции связей вала |
С раскладываем |
на |
три |
|
|
|
|
21

составляющие: XC , YC , ZC , направленные вдоль координатных осей. Реакция подшипника К лежит в плоскости, перпендикулярной оси вала, и ее состав-
ляющими будут вектора X K , ZK , направленные вдоль координатных осей x, z.
Натяжение нити T направлено вдоль нити от точки К и по модулю равно весу груза. Действие на вал внешних сил и реакций связи показано на рис. 1.15.
Внешние силы, действующие на вал, и реакции связей составляют произ-
вольную пространственную систему сил эквивалентную нулю
( P, F, X K , ZK , T , XC , YC , ZC , М) ∞ 0, для которой уравнения равновесия
å Fkx = 0 , å Fky = 0 , å Fkz = 0 ,
åM x (Fk ) = 0 , åM y (Fk ) = 0, åM z (Fk ) = 0.
Для удобства при составлении уравнений равновесия изобразим вал вме-
сте с действующими на него силами в проекциях на координатные плоскости
(рис. 1.16).
Рис. 1.16. Вал и действующие на него силы в проекциях на координатные плоскости:
а – вид вала в проекции на плоскость zСx с положительного конца оси y; b – вид вала в проекции на плоскость zСy с положительного конца оси x; с – вид вала в проекции на плоскость xСy с положительного конца оси z
22

На рис. 1.16, а показаны проекции всех сил на плоскость zСx. Вычисляя моменты проекций этих сил относительно точки С, получим значения моментов исходных сил относительно оси y.
Для вычисления моментов сил относительно оси x достаточно найти мо-
менты проекций сил на плоскость zСy относительно точки С (см. рис. 1.16, b), а
вычисляя моменты проекций сил на плоскость xСy относительно точки С,
получим значения моментов сил относительно оси z .
Составляем уравнения равновесия:
å Fkx = P2 + X K + X C = 0 , åFky = F2 + YC = 0 ,
åFkz = -P1 + ZK - T + ZC - F1 = 0 ,
åM x (Fk ) = P1a − ZK 2a − T(2a + b) + F1(2a + 2b) = 0 ,
åM y (Fk ) = −F1a + TR + Pr− M = 0 ,
åM z (Fk ) = P2a + X K 2a − F2a = 0.
Подставляя исходные данные задачи, с учётом того, что |
|
P = Pcos60o = 0,5Р, P = Pcos30o = 0,87Р, |
|
1 |
2 |
F = Fcos30o |
= 0,87F, F = Fcos60o = 0,5F (см. рис. 1.16 a, b), |
1 |
2 |
получим систему уравнений: |
|
0,87 × 4 + X K + XC = 0, |
2 × 0,5 + YC = 0, - 4 × 0,5 + ZK - 3 + ZC - 2 × 0,87 = 0, |
0,5 × 4 × 0,8 -1,6ZK - 3 × 0,87(2 × 0,8 + 0,4) + 2 × 0,87(2 × 0,8 + 2 × 0,4) = 0,
- 0,87 × 0,8 + 3 × 0,6 + 4 × 0,3 - M = 0, 0,87 × 4 × 0,8 +1,6 × X K - 2 × 0,5 × 0,8 = 0.
Решая систему, найдём: |
XC = –2,24 кН, |
YC = – |
|
1 кН, |
ZC =6,39 кН, |
|||||
X K = –1,24 кН, ZK =0,35 кН, М = 2,3 |
кН·м. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Окончательно, реакция подпятника равна R |
= X |
2 |
+ Y 2 |
+ Z 2 |
= 6,84 кН, |
|||||
|
|
|
C |
|
|
C |
C |
|
C |
|
реакция подшипника RK = |
|
|
|
|
|
|
|
|
|
|
X K2 |
+ ZK2 |
= 1,29 кН. |
|
|
|
|
|
|
|
|
23
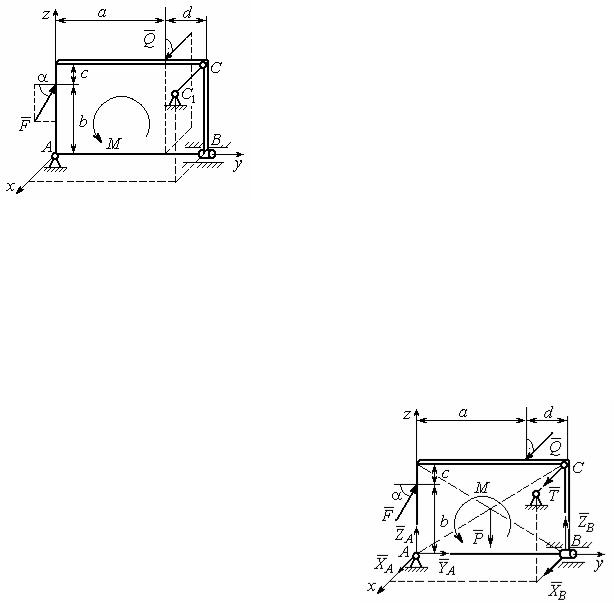
Задача 2. Плита весом Р расположена в вертикальной плоскости zАу. В
точке А плита закреплена пространственным шарниром, а в точке В на оси у
|
опирается на цилиндрический шарнир |
|
(подшипник). Плита удерживается в рав- |
|
новесии при помощи невесомого стержня |
|
СС1, прикреплённого шарниром к плите в |
|
её верхнем углу, в точке С перпендику- |
|
лярно плоскости плиты (рис. 1.17). |
|
На плиту действует сила Q , прило- |
Рис. 1.17. Равновесие плиты |
женная на краю плиты перпендикулярно |
её плоскости, и сила F , лежащая в плоскости плиты и направленная под углом
α к горизонту (см. рис. 1.17). Кроме того, в плоскости плиты на неё действует пара сил с моментом М. Найти реакции шарниров А и В и усилие в стержневой подпорке СС1 при равновесии плиты, если параметры нагрузки: Р = 1 кН,
Q = 500 Н, F = |
400 Н, М = 300 Н·м, α = 35o , |
а = 2 м, b = 1,5 |
м, с = 0,2 м, d = 0,4 м. |
Решение
Заменим связи плиты их реакциями. |
|
|
|
Реакция шарнира А раскладывается на три |
|
|
|
составляющих: X A YA , Z A по направлениям |
|
|
|
координатных осей. Направления коорди- |
Рис. 1.18. Действие сил и реакций |
||
натных осей показаны на рис. 1.17. Реакция |
|||
при равновесии плиты |
|||
|
|||
подшипника В лежит в плоскости, перпен- |
|
|
|
дикулярной оси подшипника, и ее составляющими будут вектора |
X B , ZB , на- |
||
правленные вдоль координатных осей x, z. Реакция стержня T |
направлена |
||
вдоль стержня. Действие сил и реакций показано на рис.1.18. |
|
||
24

Пространственная система сил, действующих на плиту, является уравно-
вешенной: ( P, F, X B , ZB , T , X A , YA , ZA , М) ∞ 0. Уравнения равновесия:
å Fkx = 0 , å Fky = 0 , å Fkz = 0 ,
åM x (Fk ) = 0 , åM y (Fk ) = 0, åM z (Fk ) = 0.
Ввычислениях моментов сил относительно осей будем считать момент положительным, если при взгляде со стороны положительного направления оси, сила вращает тело (плиту) против хода часовой стрелки. Получим
åFkx = 0 , X A + Q + X B + T = 0,
åFky = 0 , YA + Fcosa = 0,
åFkz = 0 , Z A + Fsina - P + ZB = 0
åM x (Fk ) = 0 , - Fcosa × b - P × 0,5(a + d) + ZB (a + d) + M = 0,
åM y (Fk ) = 0, Q × (b + c) + T × (b + c) = 0,
åM z (Fk ) = 0, - Q × a - T × (a + d) - X B × (a + d) = 0.
Подставив исходные данные задачи, получим систему уравнений
X A + 500 + X B + T = 0, |
YA + 400 × 0,82 = 0, Z A + 400 × 0,57 -1000 + ZB = 0, |
||
- 400 × |
0,82 |
×1,5 -1000 × 0,5 |
× 2,4 + ZB × 2,4 + 300= 0, |
500 ×1,7 |
+ T ×1,7 = 0, - 500 |
× 2 - T × 2,4 - X B × 2,4= 0, |
|
откуда находим значения составляющих реакций
T = −500 Н, X B = 83,33 Н, ZB = 580 Н,
X A = -83,33 Н, YA = -328 Н, Z A =192 Н.
Полные реакции пространственного шарнира А:
RA = 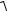
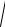 X A2 + YA2 + Z A2 = 389,09 Н,
X A2 + YA2 + Z A2 = 389,09 Н,
цилиндрического шарнира В: RB = 
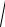 X B2 + ZB2 = 585,95 Н.
X B2 + ZB2 = 585,95 Н.
25

2. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
Кинематикой называется раздел механики, в котором изучаются свойст-
ва движения материальных тел без учета их масс и действующих на них сил.
2.1. Кинематика точки. Основные параметры движения точки
Кривая, которую описывает движущаяся точка, называется траекторией
точки. Движение точки может быть задано векторным, координатным или ес-
тественным способами.
Векторный способ основан на определении положения точки ее радиу-
сом-вектором в виде векторного уравнения r = r (t) . При координатном спосо-
бе задания движения точки положение точки определяется ее координатами,
заданными для каждого момента времени: x = x(t) , y = y(t) , z = z(t). Естест-
венный способ задания движения используется, если заранее известна траекто-
рия движения точки. Тогда положение точки однозначно определяется длиной дуги OM = S(t) , отсчитываемой от некоторой фиксированной точки О, приня-
той за начало отсчета.
Мгновенная скорость, или скорость точки в данный момент времени,
является векторной величиной и определяется как производная по времени от
радиуса-вектора точки: = r& . Вектор скорости точки V всегда направлен по ка-
V r
сательной к траектории в сторону движения точки.
При координатном способе задания движения величины проекций векто-
ра скорости V на координатные оси определяются как производные по времени от соответствующих координат: Vx = x& , Vy = y& , Vz = z& . Модуль вектора скоро-
сти: V = 
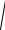 Vx2 + Vy2 + Vz2 . При естественном способе задания движения вектор
Vx2 + Vy2 + Vz2 . При естественном способе задания движения вектор
скорости точки определяется равенством: = &r , где S S(t) – закон измене-
V Sτ =
26

ния длины дуги, τ –единичный вектор касательной к траектории движения, на-
правленный в сторону возрастающих расстояний. |
|
|
|
||||
Величина V = |
|
& |
|
называется алгебраической скоростью точки. При |
& |
> 0 |
|
|
|
||||||
|
S |
|
S |
||||
вектор скорости V |
|
направлен по единичному вектору τ |
– в сторону возрас- |
||||
тающих расстояний. При S& < 0 он имеет направление, противоположное еди-
ничному вектору τ , т. е. в сторону убывающих расстояний.
Мгновенное ускорение, или ускорение точки в данный момент времени,
является векторной величиной и определяется как производная по времени от вектора скорости точки или как вторая производная от радиус-вектора точки:
r |
r |
r |
|
|
|
|
|
& |
|
|
|
|
|
||
|
|
&& |
|
|
|
|
|
a =V = r . При координатном способе проекции вектора ускорения a на коор- |
|||||||
динатные оси – величины ax , ay , az – определяются равенствами: |
ax |
& |
= x , |
||||
=Vx |
|||||||
|
|
|
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
& |
& |
2 |
|
2 |
2 |
|
|
|
+ ay |
+ az . |
||||
ay = Vy = &y&, az = Vz = &z&. Модуль вектора ускорения равен: a = ax |
|||||||
При естественном способе задания движения вектор ускорения точки a
раскладывается на две взаимно перпендикулярные составляющие an и aτ , па-
раллельные осям n и τ естественной системы координат, и представляется в виде равенства a = aττ + ann , или a = aτ + an , где τ – единичный направляю-
щий вектор оси, касательной к траектории (касательная ось); n – единичный
направляющий вектор главной нормали траектории. Величина an называется
нормальным ускорением точки и вычисляется по формуле: an = |
V 2 |
, где ρ – |
|
ρ |
|||
|
|
радиус кривизны траектории. (У окружности радиус кривизны равен её радиусу,
у прямой линии – бесконечности.) Вектор an нормальной составляющей уско-
рения всегда направлен к центру кривизны траектории. При движении по ок-
ружности радиус кривизны траектории равен радиусу окружности, а центр кри-
визны траектории совпадает с центром окружности. Величина aτ называется
касательным ускорением и равна модулю второй производной от заданного
27
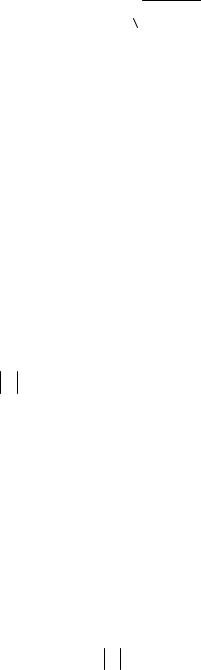
закона изменения длины дуги: aτ = |
|
&& |
|
, где S = S(t) – закон изменения |
дли- |
||
|
|
||||||
|
S |
|
|||||
ны дуги. Направление вектора касательного ускорения aτ |
зависит от знака |
||||||
&& |
&& |
|
|
|
|
|
|
второй производной S . При S > 0 вектор aτ в направлен в сторону возрастаю- |
|||||||
щих расстояний, по направлению единичного вектора τ . При |
&& |
|
|||||
S < 0 – в сторону |
|||||||
убывающих расстояний |
(противоположно единичному вектору τ ). Вектор пол- |
||||||
ного ускорения a направлен по диагонали прямоугольника, |
построенного на |
||||||
векторах an и aτ Модуль вектора ускорения равен: a = 
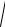 an2 + aτ2 .
an2 + aτ2 .
2.2. Вращение тела вокруг неподвижной оси
Движение тела, при котором все точки некоторой его прямой остаются неподвижными, называется вращательным, а указанная прямая называется осью вращения. Вращение тела задается углом поворота ϕ = ϕ(t) подвижной плоскости, связанной с телом, относительно некоторого ее начального положе-
ния. Направление вращения с возрастанием угла поворота считается положи-
тельным.
Величина угловой скорости вращения тела равна модулю производной от угла поворота тела по времени: ω = ϕ . Направление угловой скорости вра-
щения тела зависит от знака производной ϕ& . При ϕ& > 0 вращение происходит в
положительном направлении, в сторону возрастания угла поворота. При ϕ& < 0
– в отрицательном. Направление угловой скорости обычно показывают дуговой стрелкой вокруг оси вращения. Вектор угловой скорости ω направлен вдоль оси вращения в сторону, откуда вращение тела видно против хода часовой стрелки.
Величина углового ускорения при вращении тела равна модулю второй производной от угла поворота тела по времени: ε = ϕ&& . Если ϕ&& одного знака с
28
ϕ& , то угловое ускорение ускоряет вращение тела. Если разных знаков, то угло-
вое ускорение замедляет вращение.
При вращательном движении тела все его точки движутся по окружно-
стям, радиусы которых равны расстояниям от выбранной точки до неподвиж-
ной оси. Скорость точки вращающегося твердого тела (в отличие от угловой скорости тела) называют линейной, или окружной скоростью точки. Величина скорости рассчитывается по формуле: V = ω h , где ω – величина угловой ско-
рости тела; h – расстояние от точки до оси вращения. Вектор скорости точки лежит в плоскости описываемой точкой окружности и направлен по касатель-
ной к ней в сторону вращения тела. Отношение скоростей двух точек вращаю-
щегося тела равно отношению расстояний от этих точек до оси: |
VM1 |
= |
h1 |
. |
|
|
|
||||
|
V |
M 2 |
|
h |
|
|
|
2 |
|
||
Ускорение точки вращающегося твердого тела рассчитывается как ус-
корение точки при естественном способе задания движения в виде суммы век-
торов касательного и нормального ускорений: aM = aτ + an . Величины каса-
тельного, нормального и полного ускорений точки вращающегося тела, соот-
ветственно, равны: aτ = ε h , |
an = ω2h , aM = |
aτ2 + an2 |
, где ω , ε – угловая |
скорость и угловое ускорение |
тела; h – расстояние от точки до оси вращения. |
||
2.3. Плоскопараллельное движение твёрдого тела
Плоскопараллельным, или плоским движением твердого тела, назы-
вается такое движение, при котором все точки тела движутся параллельно неко-
торой неподвижной плоскости. Плоское движение представляется в виде суммы мгновенного поступательного движения, при котором все точки плоской фигу-
ры движутся со скоростью выбранной точки-полюса, и мгновенного враща-
тельного движения вокруг этого полюса.
29
